Otimização Combinatória
Prof. Flávio Keidi Miyazawa
Problemas de otimização, na sua forma geral, têm como objetivo maximizar ou minimizar uma função definida sobre um certo domínio. A teoria clássica de otimização trata do caso em que o domínio é infinito. Já no caso dos chamados problemas de otimização combinatória, o domínio é tipicamente finito; além disso, em geral é fácil listar os seus elementos e também testar se um dado elemento pertence a esse domínio. Ainda assim, a idéia ingênua de testar todos os elementos deste domínio na busca pelo melhor mostra-se inviável na prática, mesmo para instâncias de tamanho moderado.
Como exemplos clássicos de problemas de otimização combinatória podemos citar o problema do caixeiro viajante, o problema da mochila, o problema da cobertura mínima por conjuntos, o problema da floresta de Steiner e o problema da satisfatibilidade máxima. Todos surgem naturalmente em aplicações práticas, tais como o projeto de redes de telecomunicação e de circuitos VLSI, o empacotamento de objetos em containers, a localização de centros distribuidores, o escalonamento e roteamento de veículos, etc. Outras áreas de aplicação incluem a estatística (análise de dados), a economia (matrizes de entrada/saída), a física (estados de energia mínima), a biologia molecular (alinhamento de DNA e proteínas, inferência de padrões), etc.
Estratégias que tem tido sucesso no tratar destes problemas envolvem métodos em programação inteira, algoritmos probabilísticos e algoritmos de aproximação.
Descrição informal de alguns destes problemas:
Projeto de Redes com Restrições de Conectividade
Projeto do Caminho Mínimo
Problema do Caixeiro Viajante
Problema do Roteamento de Veículos
Corte de Placas
Escalonamento de Tarefas
Problemas de Classificação e Particionamento
Problemas de Corte e Empacotamento
Atribuições de Freqüências em Telefonia de Celular
 Projeto de Redes com
Restrições de Conectividade
Projeto de Redes com
Restrições de ConectividadeSuponha que você está projetando uma rede de computadores com algumas restrições de conectividade. Nesta rede, alguns computadores importantes devem sempre poder se comunicar entre eles, outros são menos importantes e podem servir apenas como um nó intermediário para conectar os computadores principais. Com este conjunto de restrições em mãos e o custo para conectar diretamente dois computadores através de fibras óticas, projetar a rede de menor custo, respeitando as restrições de conectividade.
Podemos também considerar adicionar
restrições de segurança contra falhas. Por
exemplo, a rede poderia ser construída de tal maneira
que mesmo que
uma conexão ligando dois computadores fique temporariamente fora
do
ar, a rede projetada deve permitir uma rota alternativa que ligue
todos os computadores principais.
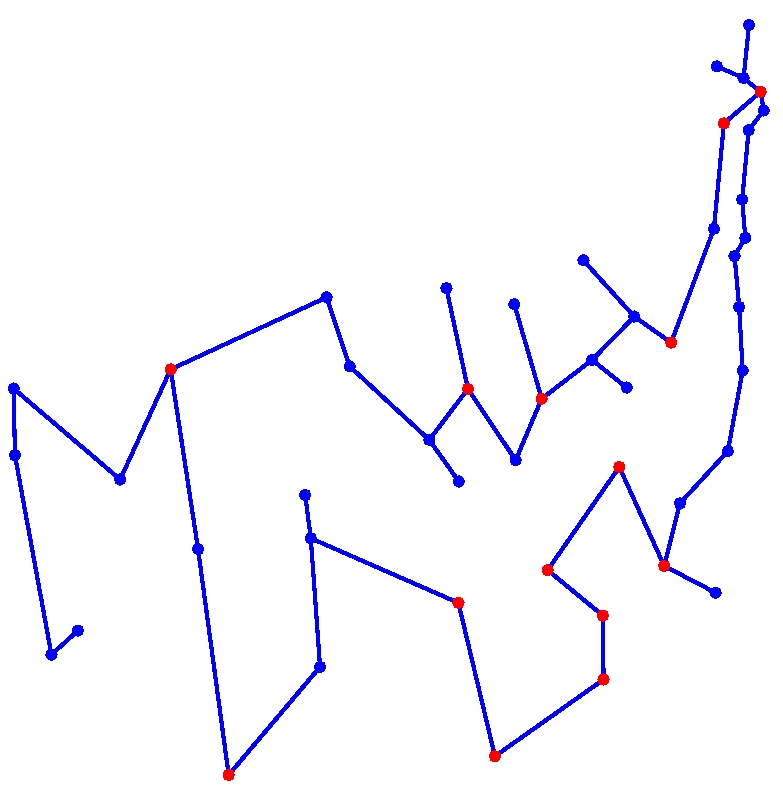
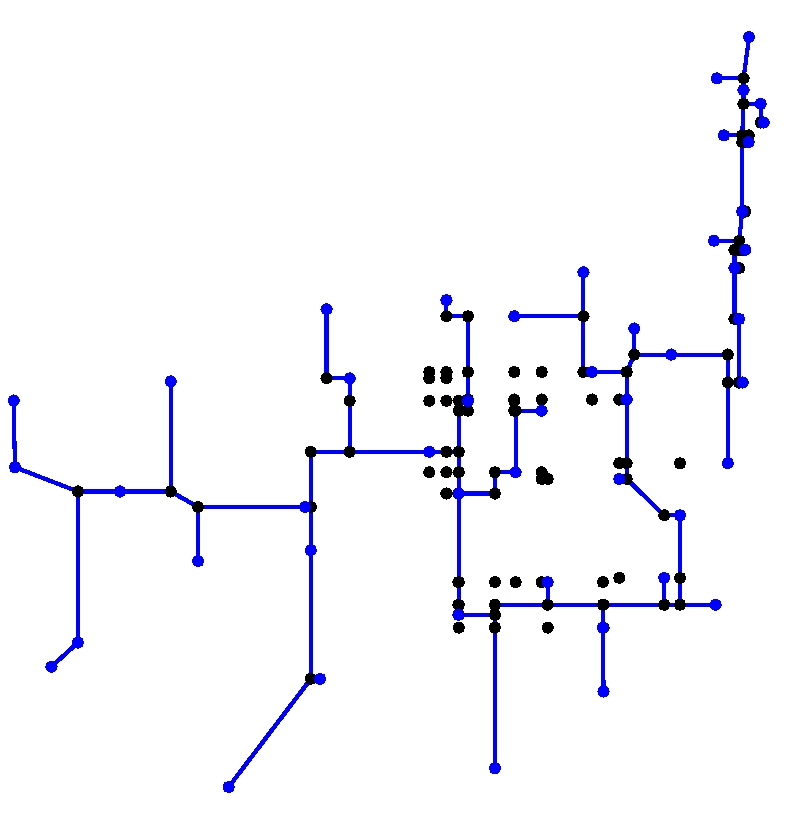
Em circuitos VLSI, há restrições na forma das ligações, que muitas vezes devem ser horizontais ou verticais. Os pontos em azul, da figura acima devem estar ligados por uma rede.
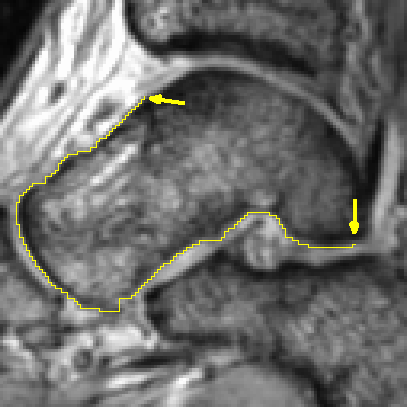
Exemplo do Problema do Caminho Mínimo aplicado à segmentação de imagens.
 Problema do Caixeiro Viajante
Problema do Caixeiro Viajante
Uma fábrica de
componentes eletrônicos precisa soldar milhares de placas de
circuitos impressos. Para agilizar, todas as placas de mesmo tipo são
soldadas uma após a outra, em pontos previamente especificados. O
objetivo é saber qual o trajeto das posições que a máquina de solda
deve percorrer para que gaste o menor tempo possível em cada
placa. Note que qualquer ganho de tempo neste trajeto pode ser
crucial para se soldar as milhares de placas em pouco tempo.
Agora, suponha que você quer conhecer algumas cidades do Estado de Sao Paulo e a partir de uma cidade inicial, percorrer outras cidades e voltar à cidade de inicial, gastando o menor tempo possível.
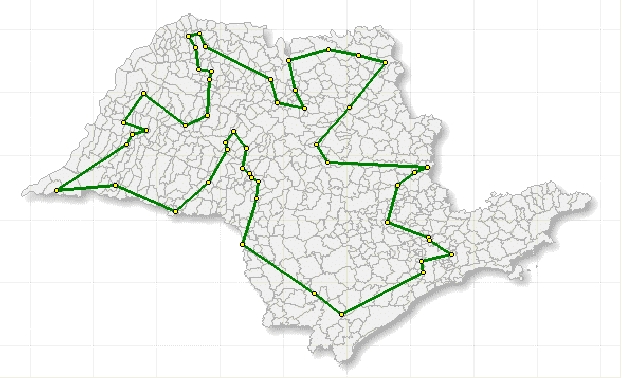
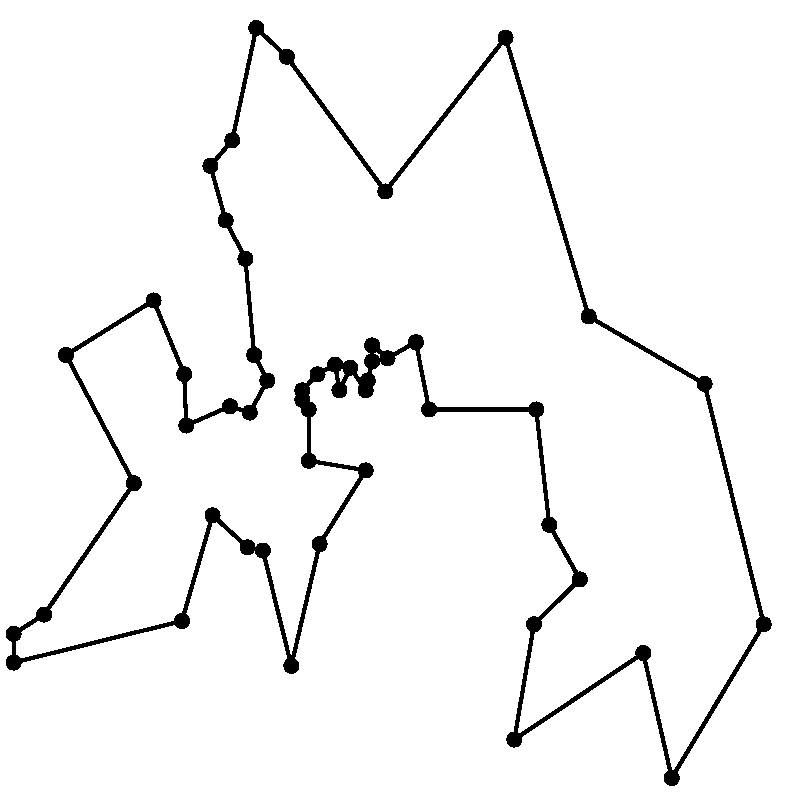
Exemplo de rota ligando 52 pontos de um parque na cidade de Berlin.
Veja mais sobre este problema na página sobre o Problema do Caixeiro Viajante.
Problema de Roteamento de Veículos
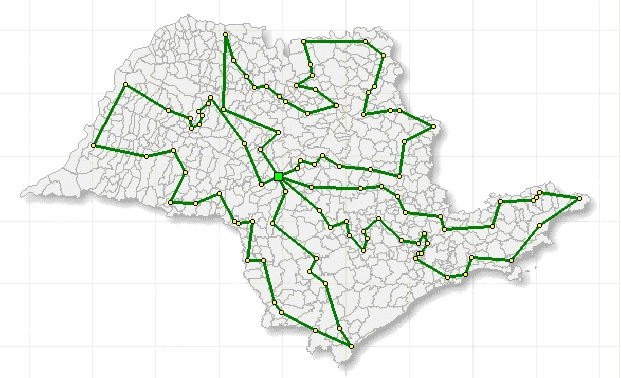
Considere que você tem um depósito (matriz) de onde saem caminhões carregados de certos produtos e devem passar por algumas cidades. Porém, em cada cidade o caminhão deve entregar certos produtos e há uma capacidade máxima que o caminhão pode carregar em cada viagem. O objetivo é minimizar o gasto total (digamos em kilometros rodados) para entregar todos os produtos e respeitando a capacidade do caminhão. Exemplo de rotas:
Exemplo: Classificação dos pixels de uma imagem. A esquerda temos uma imagem com 50% de degradação e a direita, a imagem com seus pixels classificados em preto ou branco.
 Problemas de Corte e Empacotamento
Problemas de Corte e Empacotamento
Considere agora que você está construindo um prédio. As janelas e
divisórias de vidro do prédio são necessárias em quantidade e tamanhos
diferentes. A construtora faz o pedido de compra a uma vidraçaria,
especificando as dimensões e quantidades de cada item. A vidraçaria
deve cortar estes pedaços a partir de placas de vidro de tamanhos
fixos, que são fornecidas pelo
fabricante de vidro. Para minimizar os custos, o objetivo da
vidraçaria é usar o menor número destas placas.

Exemplo de corte de retalhos retangulares a partir de placas.
Note que um problema relacionado, mas agora tridimensional, é
o problema de empacotar objetos dentro de containeres, de maneira a
maximizar a carga no container, ou minimizar a quantidade de
conteineres usados para transportar determinado conjunto de
objetos.
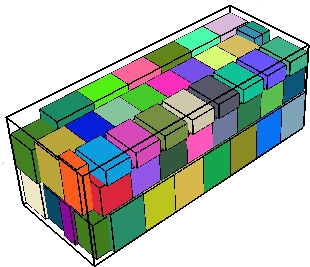
Exemplo de empacotamento de caixas em contêineres.
Se você quiser saber mais sobre este tipo de problema, veja a página de Problemas de Corte e Empacotamento
 Atribuições de
Freqüências em Telefonia de Celular
Atribuições de
Freqüências em Telefonia de Celular
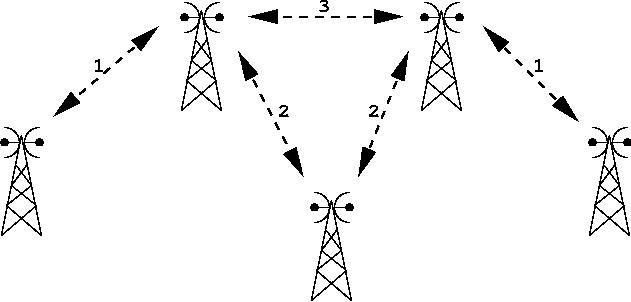
Considere agora uma empresa que tem várias torres (antenas) que cobrem
uma determinada região por onde trafegam usuários de telefone celular.
Quando duas antenas muito próximas recebem as mesmas freqüencias, a
região que sofre a cobertura destas antenas apresenta muita
interferência. O objetivo é atribuir as freqüências (de quantidade
limitada) para as antenas de maneira a minimizar a interferência total
da atribuição.
Você deve ter percebido que estes problemas de otimização combinatória podem ser facilmente formulados e compreendidos. Nestes problemas, temos como objetivo maximizar ou minimizar uma função definida sobre um domínio tipicamente finito. Mas não se iluda, apesar de finito, este domínio é para muitos problemas, extremamente grande e na maioria das vezes é computacionalmente inviável percorrer todo este domínio.
Algumas das principais linhas para se atacar problemas NP-difíceis são:
Algoritmos de Aproximação
Algoritmos Probabilísticos
Algoritmos Híbridos
Programação Linear Inteira
Programação Quadrática
Programação Semidefinida
Heurísticas