MO417 - Ata da Aula [Programação Dinâmica]


Ata: Aula do dia 02/04/2003
Assunto: Capítulo 15 (Tópicos 15.1 e 15.2)
Professor: João Meidanis
Redator: Thiago Alves da Silva
 
A figura sobre linha de montagem foi obtida do site http://www.introductiontoalgorithms.com e é reproduzida aqui seguindo as normas vigentes de copyright ( http://www.mcgraw-hill.com/copyrttm.htm ).

Tópicos

1. Introdução

2. Programação de linha de montagem
    2.1. A estrutura de uma solução ótima
    2.2. Uma solução recursiva
    2.3. Cálculo do valor de uma solução ótima
    2.4. Construção de uma solução ótima

3. Multiplicação de cadeias de matrizes
    3.1. A estrutura de uma solução ótima
    3.2. Uma solução recursiva
    3.3. Cálculo do valor de uma solução ótima
    3.4. Construção de uma solução ótima

4. Conclusão

5. Referências Bibliográficas
 

1. Introdução

A programação dinâmica é uma importante técnica para o projeto e análise eficiente de algoritmos. Como o método de dividir e conquistar, ela resolve problemas combinando as soluções para subproblemas. Ela é aplicável quando os subproblemas não são independentes, isto é, quando os subproblemas compartilham subsubproblemas. Um algoritmo de programação dinâmica resolve cada subproblema uma vez só e então grava sua resposta em uma tabela, evitando assim o trabalho de recalcular a resposta toda vez que o subsubproblema é encontrado. Esse método pode às vezes transformar facilmente algoritmos de tempo exponencial em algoritmos de tempo polinomial.

O desenvolvimento de um algoritmo de programação dinâmica pode ser desmembrado em uma seqüência de 4 tapas:

1. Caracterizar a estrutura de uma solução ótima
2. Definir recursivamente o valor de uma solução ótima
3. Calcular o valor de uma solução ótima
4. Construir uma solução ótima a partir de informações calculadas

Veremos a seguir dois exemplos onde a programação dinâmica é empregada com sucesso.
 

2. Programação de linha de montagem

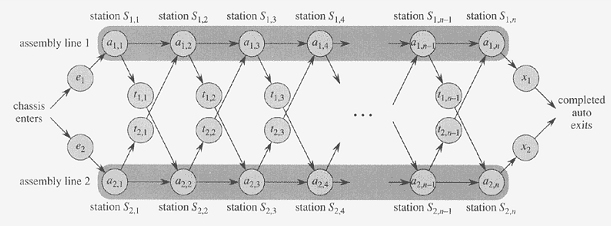
Nesse primeiro exemplo temos uma fábrica com duas linhas de montagens. Um chassi de automóvel entra em cada linha de montagem, tem as peças adicionadas a ele em uma série de estações, e um automóvel pronto sai no final da linha. Cada linha de montagem possui n estações, numeradas com j = 1, 2, ..., n. Cada linha de montagem é numerada com i = 1 ou 2. Com isso temos S_i,j como sendo a j-ésima estação na linha i. A j-ésima estação da linha 1 (S_1,j) executa a mesma função que a j-ésima estação na linha 2 (S_2,j). Porém, as estações foram construídas em épocas diferentes e com tecnologias diferentes, de forma que o tempo exigido em cada estação varia, até mesmo as estações na mesma posição nas duas linhas. Denotamos o tempo de montagem exigido na estação S_i,j por a_i,j. Além disso, temos um tempo de entrada e_i, um tempo de saída x_i e um tempo para transferir um chassi de uma linha de montagem para outra depois da passagem pela estação S_i,j, que é t_i,j. É importante ressaltar que uma transferência pode ocorrer até quando a estação for n-1, pois após a n-ésima estação, a montagem se completa.

Visto isso, podemos definir o problema que será resolvido pela programação dinâmica, que é determinar que estações escolher na linha 1 e quais escolher na linha 2 para minimizar o tempo total de passagem de um único automóvel pela fábrica.

Caso fossemos determinar o caminho mais rápido pela fábrica enumerando todos os modos possíveis e calculando quanto tempo cada um deles demora, levaríamos o tempo de Ômega(2^n), que é inviável quando n é grande.

Dicas do Professor:
O professor chama a atenção para a definição do custo, que nesse caso é apenas o tempo.
Analisando a representação gráfica da linha de montagem, o professor alerta para que nos preocupemos com as entradas: "e's", "a's", "t's" e os "x's", pois é o que o programa receberá.

2.1. A estrutura de uma solução ótima

Esta é a primeira etapa do paradigma da programação dinâmica, caracterizar a estrutura de uma solução ótima.

No caso da programação da linha de montagem, uma solução ótima para um problema (encontrar o caminho mais rápido passando pela estação S_i,j) contém em seu interior uma solução ótima para subproblemas (encontrar a passagem mais rápida por S_1,j-1 ou S_2,j-1). Essa é a propriedade da subestrutura ótima.

Concluindo, temos que para resolver o problema de encontrar o caminho mais rápido através da estação j de uma das linhas, resolvemos os subproblemas de encontrar os caminhos mais rápidos pela estação j -1 em ambas as linhas. Isso permite que você construa a solução pouco a pouco.

O professor completa essa análise dizendo que a propriedade da subestrutura ótima verifica-se neste caso da seguinte forma: um prefixo B de uma solução ótima A também é uma solução ótima para o subproblema correspondente, porque se ela não fosse, existiria outra melhor que poderia substituí-la, melhorando também a solução A. Para o problema em questão, podem existir várias soluções com o mesmo tempo, ou seja, a ótima não é necessariamente única.

2.2. Uma solução recursiva

Nessa etapa buscamos uma solução recursiva para o problema em questão.

De acordo com nosso problema, temos que o caminho mais rápido até completar a estação S_1,j é o caminho mais rápido até completar a estação S_1,j-1, e depois passar diretamente pela a estação S_1,j, ou o caminho mais rápido até completar a estação S_2,j-1, uma transferência da linha 2 para a linha 1, e depois passar pela estação S_1,j (toma-se o que for menor dos dois). Um racioncínio análogo vale para completar S_2,j. As recorrências a seguir mostram isso:
              | e_1 + a_1,1                                                             se j = 1,
f_1[j] = {
              | min(f_1[j-1] + a_1,j , f_2[j-1] + t_2,j-1 + a_1,j)      se j >= 2.
              | e_2 + a_2,1                                                            se j = 1,
f_2[j] = {
              | min(f_2[j-1] + a_2,j , f_1[j-1] + t_1,j-1 + a_2,j)    se j >= 2.
f_i[j] é o tempo mais rápido possível para levar um chassi desde o ponto de partida até a estação S_i,j.

Por fim temos que o tempo mais rápido para levar um chassi por todo o percursso na fábrica é:
min(f_1[n] + x_1, f_2[n] + x_2).

Discussão em aula:

TEMPO(n)
Se (f_1(n) + x_1) < (f_2(n) + x_2)
    tempominimo = f_1(n) + x_1
    saidaporlinha = 1
Senao
    tempominimo = f_2(n) + x_2
    saidaporlinha = 2
Fim-se

f_i(n)
Se (n = 1)
    devolver a_i(1) + e_i
Se f_i(n-1) + a_i(n) < f_î(n-1) + t_î(n-1) + a_i(n)
    devolver f_i(n-1) + a_i(n)
Fim-se
devolver f_î(n-1) + t_î(n-1) + a_i(n)
Obs.: A notação î, empregada no algoritmo, significa que î valerá 1 se i for igual a 2 ou 2 se i for igual a 1.

2.3. Cálculo do valor de uma solução ótima

Um algoritmo recursivo para a solução deste problema gera muitas chamadas recursivas, tendo como conseqüência disso, seu tempo de execução exponencial em n. Agora, um algoritmo utilizando a técnica de programação dinâmica, consegue calcular o caminho mais rápido pela fábrica e o tempo que ele demora, no tempo Theta(n).
FASTEST-WAY(a, t, e, x, n)
1   f_1[1] <- e_1 + a_1,1
2   f_2[1] <- e_2 + a_2,2
3   for j <- 2 to n
4         do if f_1[j-1] + a_1,j <= f_2[j-1] + t_2,j-1 + a1,j
5             then  f_1[j] <- f_1[j-1] + a_1,j
6                           l_1[j] <- 1
7             else  f_1[j] <- f_2[j-1] + t_2,j-1 + a_1,j
8                           l_2[j] <- 2
9           if f_2[j-1] + a_2,j <= f_1[j-1] + t_1,j-1 + a_2,j
10            then f_2[j] <- f_2[j-1] + a_2,j
11                         l_2[j] <- 2
12            else f_2[j] <- f_1[j-1] + t_1,j-1 + a2,j
13                         l_2[j] <- 1
14   if f_1[n] + x_1 <= f_2[n] + x_2
15      then  f* = f_1[n] + x_1
16               l* = 1
17      else  f* = f_2[n] + x_2
18               l* = 2

O professor Meidanis conclui esse tópico chamando a atenção para o uso de 4 vetores no lugar da recursão. Vetores esses: f_1, f_2, l_1 e l_2.

2.4. Construção de uma solução ótima

A construção da solução ótima é mostrada no procedimento PRINT-STATIONS, que imprime as estações usadas, em ordem decrescente de número de estações.
PRINT-STATIONS(l,n)
1  i <- l*
2  imprimir "linha" i ",estação" n
3  for j <- n downto 2
4        do i <- l_i[j]
5        imprimir "linha" i ",estação" j-1
O professor adverte sobre a saída desse procedimento, isto é, ele imprime a ordem inversa, da última estação para a primeira.

 

3. Multiplicação de cadeias de matrizes

Nesse caso não estamos realmente multiplicando matrizes. O objetivo é apenas determinar uma ordem para multiplicar matrizes que minimize o número de multiplicações escalares. O modo como a cadeia de matrizes é colocada entre parênteses pode ter um impacto dramático sobre o custo de avaliação do produto.

Se fossemos utilizar um algoritmo de força bruta para verificar exaustivamente todas as possíveis colocações entre parênteses, obteríamos a seguinte recorrência:
            | 1                                          se n = 1,
P(n) = {
            |             n-1
            | P (n) = soma P(k)P(n-k)          se n >= 2.
                          k=1
A solução para essa recorrência é Ômega(2^n). Portanto, o número de soluções é exponencial em n. Com isso verificamos que o método da força bruta para se determinar a colocação ótima dos parênteses é ineficiente.

Antes de iniciarmos nossa busca por uma solução eficiente utilizando programação dinâmica, o professor chama a atenção para a definição da entrada, que nesse caso é um vetor de 0 até n, que contém inteiros Pi. O vetor inicia de 0, pois a dimensão da matriz Ai é Pi-1 * Pi. Também devemos nos preocupar em definir a saída, nesse caso como sendo duas matrizes m e s, onde somente a diagonal principal será utilizada.

3.1. A estrutura de uma solução ótima

O primeiro passo é caracterizar a estrutura de uma solução ótima. Vamos adotar a notação Ai..j para a matriz que resulta da avaliação do produto Ai.Ai+1...Aj. Para obter a solução do problema proposto, devemos obter A1..n, que pode ser obtido pelo produto de A1..k.Ak+1..n, cujo custo ótimo é obtido pela soma do custo de A1..k com Ak+1..n, mais o custo do produto delas. A subcadeia A1..k deve ter parentização ótima, do contrário poderíamos substituí-la, por outra com o custo menor que o ótimo.

Logo, uma solução ótima para uma instância do problema contém soluções ótimas para as sub-instâncias do mesmo problema, o que permite o emprego da programação dinâmica.

3.2. Uma solução recursiva

Deve-se definir uma expressão recursiva para a solução ótima em função das sub-instâncias. Será utilizada uma tabela m_ij 1 <= i <= j <= n, para armazenar a solução ótima para Ai..j. O valor m[i,i] = 0, pois Ai..i = Ai, não havendo a necessidade de qualquer cálculo.

Para i < j, podemos usar a estrutura ótima delineada na etapa 1. Assim Ai..j pode ser dividido em duas partes Ai..k e Ak+1..j, onde i <= k < j. Então m[i,j] é igual ao menor custo para calcular Ai..k e Ak+1..j, mais o custo para multiplicar essas duas matrizes. O custo para multiplicar Ai..k.Ak+1..j exige Pi-1.Pk.Pj multiplicações escalares.

Temos a seguinte definição recursiva para o custo mínimo de colocar entre parênteses o produto AiAi+1...Aj:
             | 0                                                           se i = j,
m[i,j] = {
             | min{m[i,k] + m[k+1,j] + Pi-1.Pk.Pj}     se i < j.
             | i <= k < j
Os valores de m[i,j] fornecem os custos de soluções ótimas para subproblemas, mas não informações para a construção de uma solução ótima. Para facilitar a indicação de uma parentização ótima, basta armazenar na matriz s[i,j] o valor de k usado para o valor ótimo de m[i,j], ou seja m[i,j] = m[i,k] + m[k+1,j] + Pi-1.Pk.Pj.

3.3. Cálculo do valor de uma solução ótima

Usando a programação dinâmica passamos a ter Theta(n^2) subproblemas (basta observar que m[i,j] armazena os valores ótimos desses subproblemas), bem mais eficiente que o algoritmo de força bruta que é exponencial em n.

Neste ponto deve-se elaborar um algoritmo para a solução do problema, fazendo os cálculos de tal forma que nenhuma solução seja requisitada antes que a mesma já tenha sido calculada. O procedimento a seguir utiliza uma tabela auxiliar m[1..n,1..n] para armazenar os custos de m[i,j] e uma tabela auxiliar s[1..n,1..n] que registra qual índice de k alcançou o custo ótimo no cálculo de m[i,j]. Na construção de uma solução ótima usaremos a tabela s.
MATRIX-CHAIN-ORDER(P)
1   n <- comprimento[P] -1
2   for i <- 1 to n
3        do m[i,j] <- 0
4   for l <- 2 to n                          // l é o comprimento da cadeia
5        do for i <- 1 to n - l + 1
6           do j <- i + l - 1
7                  m[i,j] <- infinito
8               for k <- i to j - 1
9                    do q <- m[i,k] + m[k+1,j] + Pi-1.Pk.Pj
10                       if q < m[i,j]
11                           then m[i,j] <- q
12                                      s[i,j] <- k
13   return m  e s
O tempo de execução do procedimento, O(n^3), pode ser determinado simplesmente observando a estrutura de loop aninhados.

3.4. Construção de uma solução ótima

A construção de uma solução ótima para o problema de multiplicação de cadeias de matrizes se baseia na tabela s. Cada entrada s[i,j] registra o valor de k tal que a colocação ótima de parênteses de AiAi+1..Aj divide o produto entre Ak e Ak+1. Desse modo, sabemos que a multiplicação de matrizes final no cálculo ótimo de A1..n, é A1..s[1,n]As[1,n]+1..n. As multiplicações de matrizes anteriores podem ser calculadas recursivamente, pois s[1,s[1,n]] determina a última multiplicação de matrizes no cálculo de A1..s[1,n], e s[s[1,n]+1,n] determina a última multiplicação de matrizes no cálculo de As[1,n]+1..n. O procedimento recursivo PRINT-OPTIMAL-PARENS mostra isso.
PRINT-OPTIMAL-PARENS(s,i,j)
1   if i = j
2      then print "A"i
3      else print "("
4              PRINT-OPTIMAL-PARENS(s,i,s[i,j])
5              PRINT-OPTIMAL-PARENS(s,s[i,j]+1,j)
6              print ")"
A chamada inicial deve ser PRINT-OPTIMAL-PARENS(s,1,n), onde n é o número de matrizes.
 

Discussão em aula:

 

4. Conclusão

O professor Meidanis conclui destacando as características da programação dinâmica: o problema precisa ter a propriedade da subestrutura ótima; então começamos com uma solução recursiva, mas ela será inviável; com isso, a transformamos em uma solução interativa, que irá ter tempo polinomial, com a característica de calcular primeiro o valor de uma solução ótima e só depois construir a solução.

Mesmo sendo considerado um assunto complexo para alguns alunos, o professor deixa claro que outros problemas serão estudados a fim de fortalecermos a idéia da programação dinâmica, e assim assimilarmos melhor o conteúdo desse capítulo.

 

5. Referências bibliográficas