Atividade de Laboratório 6
Objetivos
O objetivo desta atividade de laboratório é dar continuidade no aprendizado da linguagem de montagem da arquitetura ARM. Nesse exercício você solidificará os conceitos de construção de rotinas e iniciará no aprendizado de laços e vetores implementados em uma linguagem de baixo nível.Descrição
Introdução
Matrizes são uma estrutura muito conveniente para representar um conjunto de dados sobre um objeto qualquer, por exemplo, é comum utilizarmos uma matriz onde as linhas representam diferentes objetos (um objeto qualquer) e as colunas representam diferentes propriedades de cada objeto. Matrizes podem ser utilizadas também para armazenar os diversos pontos de uma superfície, prática muito utilizada em simulações computacionais e na resolução de problemas de otimização. Devido a sua grande utilidade, toda uma aritmética foi desenvolvida para se manipular matrizes. Nesse exercício você deverá implementar uma das operações envolvendo matrizes, a multiplicação.
A sua tarefa é: sejam duas matrizes arbitrárias Am x n e Bp x q, calcule o produto destas matrizes. As dimensões das matrizes (número de linhas e colunas de cada matriz) serão lidas via linha de comando e não serão maiores que 10, portanto para tornar o programa mais simples, você pode declarar um vetor de tamanho fixo que suporta o tamanho da maior matriz (10 x 10). Após ler as dimensões de uma matriz o seu programa deve ler o conteúdo da matriz, ou seja, o valor de cada uma das células da matriz - todos os valores serão inteiros. Primeiro será informado os dados da matriz A e em seguida os dados da matriz B. Após ler as duas matrizes o seu programa deve verificar se elas são compatíveis para multiplicação, ou seja, se o número de colunas da matriz A é igual ao número de linhas da matriz B (n == p?), caso elas não sejam seu programa deve emitir a seguinte mensagem de erro e encerrar a execução: "Matrizes incompatíveis.". Se as matrizes forem compatíveis o seu programa deverá calcular o produto e imprimir cada linha da matriz resultante em uma linha do terminal (separado por \n) onde cada uma das células da matriz deve ser impressa usando o formatador de *inteiros* "%05d".
Representação de Dados
Estruturas de dados como vetores, estruturas (structs), classes, etc. não são nada mais que artifícios providos pela linguagem de programação e pelo compilador. Quando estas estruturas são traduzidas pelo compilador muito da informação semântica delas é "descartado" e passam a ser armazenadas implicitamente nas instruções que às acessam, em outras palavras, no final tudo se torna byte(s) e o programador que deve garantir o correto acesso aos elementos da estrutura. Por exemplo, você já deve ter notado que quando você declara uma matriz em C/C++ (ex: int A[4][4]) você pode utilizar aritmética de ponteiros para acessar essa matriz como se ela fosse composta de 4 linhas com 4 colunas, 8 linhas com 2 colunas ou até mesmo como um vetor de 16 posições. Isto acontece porquê o compilador aloca de forma consecutiva na memória todos os bytes necessários para representar a matriz, linha por linha ("row major"), e deixa a cargo do programador construir a lógica correta para acessar os elementos da matriz.
Em linguagem de montagem geralmente é necessário que o programador faca como o compilador faria. Primeiro alocamos uma grande região de memória e depois utilizamos aritmética de ponteiros para indexar a linha/coluna que desejamos. Por exemplo, se quiséssemos alocar a matriz do exemplo anterior (int A[4][4]) poderíamos usar o seguinte trecho de código:
.bss A: .space 64Nesse trecho de código dizemos ao montador que vamos iniciar a definição de uma sequência de variáveis que devem ser inicializadas com zero (.bss). Em seguida declaramos um rótulo (variável) A e pedimos ao montador para reservar uma região de memória (.space) equivalente a 64 bytes (16 * 4) a partir do endereço da variável A. Dessa forma, na memória a nossa matriz de 4 x 4 estará de fato representada da seguinte forma:
>> Como o programador em linguagem de alto nível vê:
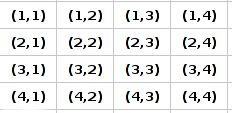
>> Como é na memória do computador:
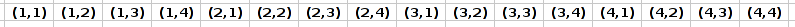
Para acessar uma posição (x,y) arbitrária dentro da matriz o programador em linguagem de montagem pode utilizar a seguinte fórmula:
A(x,y) = [ &A + X*N + Y ]
Esta fórmula requer que os índices das linhas e colunas comecem em zero, portanto a primeira célula da matriz seria (0,0) e não (1,1). Na fórmula, &A representa o endereço base da matriz e N representa o número de colunas. Usando diferentes valores para N pode-se obter diferentes interpretações para a estrutura da matriz.
Exemplo de Uso de Laços e Vetores
Como exemplo de manipulação de vetores e laços em linguagem de montagem segue abaixo um programa que pede ao usuário para informar 10 valores inteiros e em seguida escreve na tela os 10 valores lidos.
.globl main
.extern scanf
.extern printf
.data
printp: .asciz "Numero[%d] eh %d\n"
scanfp: .asciz "%d"
.bss
vetor: .space 40
.text
main:
push {ip, lr}
@ le 10 numeros inteiros
mov r3, #0x0
head1:
push {r3} @ printf/scanf suja este registrador
ldr r0, =scanfp @ pattern de leitura "%d"
ldr r1, =vetor @ endereco base do vetor
add r1, r1, r3, lsl #0x2 @ calcula *endereco* do r3-ésimo elemento
bl scanf
pop {r3} @ restaura contador
add r3, r3, #0x1 @ incrementa contador
cmp r3, #0xA @ verifica se já leu 10 números
bne head1 @ se nao tiver lido volta para o comeco do laco
@ imprime os numeros informados
mov r3, #0x0
head2:
push {r3}
ldr r0, =printp @ printf/scanf suja este registrador
mov r1, r3
ldr r2, =vetor
ldr r2, [r2, r3, lsl #0x2] @ obtem *valor* do r3-ésimo elemento
bl printf
pop {r3}
add r3, r3, #0x1
cmp r3, #0xA
bne head2
mov r0, #0x0 @ return 0 da main
pop {ip, pc} @ volta para instrucao após chamada da main
Exemplo de Entrada e Saída
Entrada:3 3 1 2 3 4 5 6 7 8 9 3 3 9 8 7 6 5 4 3 2 1Saída esperada:
00030 00024 00018 00084 00069 00054 00138 00114 00090
Entrega e avaliação
Os arquivos referentes a atividade devem ser submetidos para avaliação
utilizando o sistema Susy em:
https://susy.ic.unicamp.br:9999/mc404e/06
.
É necessário que você envie apenas o arquivo com o código em linguagem de montagem.
Note que o Susy não fará a correção automática do seu programa.