Listas

Escreva uma função que lê uma matriz $m \times n$ do teclado e guarda-a como uma lista de listas.

Escreva uma função que receba duas listas de mesmo tamanho e devolva 0 se são iguais, -1 se o primeiro vier antes lexicograficamente, e +1 caso contrário.

Faça um algoritmo que leia uma lista N. A seguir, encontre o menor elemento de N e a sua posição dentro da lista, mostrando: “O menor elemento de N é”, M, “e sua posição dentro da lista é:”, P.

Escreva um algoritmo que leia duas listas de 10 posições e faça a multiplicação dos elementos de mesmo índice, colocando o resultado em um terceira listas. Mostre a lista resultante.

Faça um algoritmo que leia uma lista S e uma variável A. A seguir, mostre o produto da variável A pela lista.

Faça um algoritmo que leia uma lista K. Troque a seguir, todos os elementos de ordem ímpar da lista com os elementos de ordem par imediatamente posteriores.

Escreva um algoritmo que leia e mostre uma lista de 20 números. A seguir, conte quantos valores pares existem na lista.

Escrever um algoritmo que lê 2 listas X e Y de mesmo tamanho. Crie, a seguir, um lista Z que seja

a) a diferença entre X e Y;

b) a soma entre X e Y;

c) o produto entre X e Y;

Escreva o lista Z a cada cálculo.

Faça um algoritmo que leia uma lista G de 10 elementos caractere que representa o gabarito de uma prova. A seguir, para cada um dos 20 alunos da turma, leia a lista de respostas (R) do aluno e conte o número de acertos. Mostre o nº de acertos do aluno e uma mensagem APROVADO, se a nota for maior ou igual a 6; e mostre uma mensagem de REPROVADO, caso contrário.

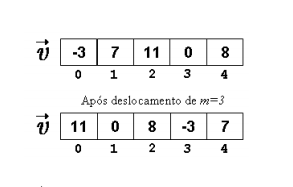
Codifique um programa que faça um deslocamento à esquerda de tamanho m vezes (m lido via teclado) em uma lista de inteiros de tamanho n (n lido via teclado). Por exemplo a seguinte figura apresenta uma lista de tamanho 5, no qual se realiza um deslocamento de tamanho 3.

Dada uma lista de inteiros de tamanho n, imprima a maior sequencia (com maior quantidade de elementos) estritamente crescente. Por exemplo, na lista: 10 20 3 4 5 6 7 50 10 100 200 300 2 3.

A maior sequencia é: 3 4 5 6 7 50 , pois possui 6 elementos.

Crie uma função que recebe uma lista e seu tamanho por parâmetro além de dois números inteiros $i$ e $j$ que são índices da lista (ou seja $0 \le i,j \le n$). A função deve então trocar os elementos das posições $i$ e $j$ entre si.

Faça um programa que lê uma lista de 30 inteiros e guarda a lista na ordem inversa que foi lido em um outra lista de saída.

Faça uma função que recebe uma lista de inteiros como parâmetro e, ao final da execução da função, a lista esteja invertida. Utilize a seguinte idéia: troque os elementos da posição 0 e 29 entre si, depois da posição 1 e 28 etc. Pense bem no critério de parada.

Escreva uma função que recebe uma lista de inteiros como parâmetro e devolve a soma dos números pares desta lista.

Faça uma função que recebe uma lista de números reais por parâmetro e devolve o desvio padrão dos números do vetor usando a seguinte fórmula:

$$ \sqrt{\frac{1}{n-1} (\sum_{i=1}^{n} x_i^2 - \frac{1}{n}(\sum_{i=1}^n x_i)^2 )} $$

onde $n$ é o número de elementos.

Modifique cada um dos seguintes algoritmos vistos em sala, para que estes ordenem um vetor em ordem decrescente de valor:

• SelectionSort

• InsertionSort

• BubbleSort

Use cada um dos algoritmos abaixo e mostre passo-a-passo, como visto em aula, os passos para ordenar a lista $(31,41,59,26,41,58,15,19)$:

• SelectionSort

• InsertionSort

• BubbleSort

Crie uma função para determinar o número total de inversões em uma lista vet. Uma inversão existe quando um elemento em uma posição $i < j$ é tal que $vet[i] > vet[j]$. Por exemplo, na lista $(10,4,6,1,2)$ existem 4 inversões para o número 10, 2 inversões para o número 4, 2 inversões para o número 6, nenhuma inversão para 1, e nenhuma para o 2. Portanto o total de inversões é 8. Modifique o algoritmo BubbleSort para computar o número de inversões em uma lista.

Escreva um programa que lê duas strings do teclado com até 80 caracteres e informa se elas são iguais.

Escreva uma função que lê uma palavra do teclado e informa se ela é palíndroma. (Exemplos de palíndromos: ARARA, RADAR, REVIVER)

O histograma de um conjunto de dados é um gráfico da frequência com que cada valor aparece. Escreva um programa que leia uma lista de tamanho informado pelo usuário e com valores inteiros entre 1 e 9 e imprima o histograma na mesma forma que o exemplo: para uma lista de tamanho 20 com os valores 1, 1, 1, 1, 2, 2, 2, 3, 3, 4, 6, 7, 8, 8, 8, 9, 9, 9, 9, 9 deverá imprimir:

+---------+
|        *|
|*       *|
|**     **|
|***    **|
|**** ****|
+---------+
 123456789

Faça uma função que devolva a soma de uma sublista $A[i..j]$ de inteiros, isso é, retorne $A[i] + ... + A[j]$.

Faça uma função que receba uma lista $A$ e devolva uma lista $A'$ tal que $A'[i] = A[0] + A[1] + ... + A[i]$.

Faça uma função que receba uma lista $A$ em devolva uma lista $A'$ tal que $A'[i] = A[i - 10] + A[i - 9] + ... + A[i]$.

Refaça as questões anteriores, mas agora a função deverá transformar a lista de entrada. Você não deve criar uma lista auxiliar e a lista passado por parâmetro de entrada é o mesmo para armazenar a saída.

Uma lista $x$ de dimensão $n$ $(3 \le n \le 100)$ é dada. Queremos transformar a lista de forma a obter somas parciais de sublistas de tamanho $3$, tal que cada elemento contenha a soma dos três elementos imediatamente anteriores. Isso é, se $y$ é obtido após a transformação de $x$, então teremos

$$ y[i] = x[i] + x[i - 1] + x[i - 2], $$

quando $i \ge 2$. Quando $i < 2$, damos a volta na lista, isso é, definimos

$$ y[0] = x[0] + x[n-1] + x[n-2] \qquad \mbox{e} \qquad y[1] = x[1] + x[0] + x[n-1]. $$

Exemplo de entrada e saída:

$$ x = [0, -2, 3, 2, 1, 2, 3, 1, 1, 1 ] \qquad \Longrightarrow\qquad x = [2, -1, 1, 3, 6, 5, 6, 6, 5, 3 ] $$

a) Escreva um algoritmo em português ou pseudocódigo para o problema. Você não deve utilizar outro vetor além da lista de entrada $x$.

b) Implemente o algoritmo anterior em Python.