Matrizes

O que o código abaixo imprime?

def mostrar_matriz(matriz):
    for linha in matriz:
        for celula in linha:
            print(celula, end=' ')
        print()

def main():
    matriz = [[0, 1, 2, 3, 4, 5, 6, 7, 8, 9],
        [10, 11, 12, 13, 14, 15, 16, 17, 18, 19],
        [20, 21, 22, 23, 24, 25, 26, 27, 28, 29],
        [30, 31, 32, 33, 34, 35, 36, 37, 38, 39],
        [40, 41, 42, 43, 44, 45, 46, 47, 48, 49],
        [50, 51, 52, 53, 54, 55, 56, 57, 58, 59]]
    mostrar_matriz(matriz)
    return

main()

Escreva uma função iterativa para decidir se uma matriz é simétrica.
Escreva uma função iterativa que, dada uma matriz real, calcule a matriz transposta.
Escreva uma função iterativa que, dada uma matriz complexa, calcule a matriz conjugada transposta.
Escreva uma função que calcule o determinante de uma matriz $3 \times 3$. (Iremos ver um algoritmo para calcular o determinante de uma matriz $n\times n$ em geral depois, mas um algoritmo mais eficiente é conteúdo de disciplinas de Álgebra Linear.)
Escreva um algoritmo que lê uma matriz $M$ e calcula as somas:

a) da primeira coluna

b) da diagonal principal

c) da diagonal secundária

d) de todos os elementos da matriz M
Projete uma função que receba uma matriz $M$ representada como listas de listas e um valor $a$. A função deve devolver uma nova matriz obtida pelo produto escalar de $a$ por $M$, i.e., $aM$.

a) Escreva uma versão em que a matriz de saída é representada de maneira convencional, usando uma lista de linhas.

b) Escreva uma versão em que a matriz de saída é representada usando lista de colunas.

c) Escreva uma versão em que a matriz de saída é representada por uma única lista de escalares, i.e., se a matriz tem dimensões $m \times n$, então a lista de escalares correspondente terá tamanho $m \cdot n$. A lista deve respeitar a ordem da matriz quando a percorremos linha a linha.
Escreva uma função que receba um número inteiro $a$ e uma matriz $M$.

a) E conte quantos valores iguais a $a$ estão na matriz.

b) E devolva uma nova matriz indicadora, isso é, uma matriz de mesma dimensão, mas com $1$ nas posições em que $M$ tem $a$ e $0$ nas demais.
Um elemento $A_{ij}$ de uma matriz $A$ é dito ponto de sela da matriz $A$ se, e somente se, $A_{ij}$ for ao mesmo tempo o menor elemento da linha $i$ e o maior elemento da coluna $j$. Faça uma função que verifique se a matriz possui ponto de sela e devolva uma tupla $(i,j)$ com sua localização, ou None caso não possua.
Uma matriz $A$ quadrada $n \times n$ é chamada de:
- triangular superior sempre que $a_{ij} = 0$ para todo $i > j$;
- triangular inferior sempre que $a_{ij} = 0$ para todo $i < j$;
- diagonal sempre que for triangular superior e inferior.
Faça uma função que classifique uma matriz.
Uma matriz de elementos inteiros é um quadrado mágico se a soma dos elementos de cada linha, a soma dos elementos de cada coluna e a soma dos elementos das diagonais principal e secundária são todas iguais. Exemplo: a matriz abaixo é um quadrado mágico.

$$ A = \begin{bmatrix} 8 & 0 & 7\\ 4 & 5 & 6\\ 3 & 10 & 2\\ \end{bmatrix} $$

Escreva uma função que verifique se uma matriz de inteiros é um quadrado mágico.
Diz a lenda que César foi um dos primeiros a codificar mensagens. Ele reorganizava o texto de suas mensagens de maneira que o texto parecia não ter sentido. Cada mensagem sempre possuía uma contagem de letras cujo total equivalia a um quadrado perfeito, dependendo de quanto César tivesse que escrever. Assim, uma mensagem com 16 caracteres usava um quadrado de quatro por quatro; se fossem 25 caracteres, seria cinco por cinco; 100 caracteres requeriam um quadrado de dez por dez, etc. Seus oficiais sabiam que deviam transcrever o texto preenchendo as casas do quadrado sempre que uma mensagem aleatória chegasse. Ao fazerem isso, podiam ler a mensagem na vertical e seu sentido se tornaria claro.

Escreva um programa que lê o tamanho de uma string e a string. Depois o programa escreve a mensagem decifrada.

Exemplo:
```
36
MEEUMOCSHMSC1T*AGU0A***L2****T*****A
```
Esta mensagem pode ser transcrita em um quadrado perfeito 6x6.
```
M E E U M O
C S H M S C
1 T * A G U
0 A * * * L
2 * * * * T
* * * * * A
```
Lendo cada coluna da matriz (desconsiderando o char ’*’), a saída deverá conter: MC102 ESTA EH UMA MSG OCULTA.
Sudoku é jogado numa malha de 9x9 quadrados, dividida em sub-malhas de 3x3 quadrados, chamada "quadrantes". O objetivo do jogo é preencher os quadrados com números entre 1 e 9 de acordo com as seguintes regras:
- Cada número pode aparecer apenas uma vez em cada linha.
- Cada número pode aparacer apenas uma vez em cada coluna.
- Cada número pode aparecer apenas uma vez em cada quadrante.
Exemplo

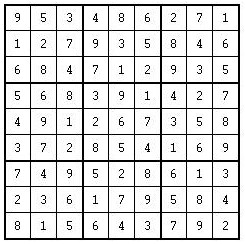
Escreva um programa que lê um jogo de Sodoku (matriz 9x9, toda preenchida com números de 1 a 9) e verifica se é um jogo válido ou não. Um jogo válido respeita as três regras acima.
Vamos fazer pixel art!

a) Desenhar é fácil. Escolha as suas figuras favoritas abaixo ou de sua preferência e faça um programa que as desenhe.

b) Reconhecer é difícil. Escreva um programa que leia alguma das figuras descritas abaixo e determine qual delas foi lida.

Retângulo de altura = 3 e largura = 7:
```
#######
#     #
#######
```
Triângulo retângulo de lado = 7:
```
#
##
# #
#  #
#   #
#    #
#######
```
Triângulo isósceles de altura = 5:
```
     #
    # #
   #   #
  #     #
 #########
```
Hexágono de lado = 3:
```
  ###
 #   #
#     #
 #   #
  ###
```
Quadriculado de lado = 4, largura = 4 e altura = 3
```
#############
#  #  #  #  #
#  #  #  #  #
#############
#  #  #  #  #
#  #  #  #  #
#############
#  #  #  #  #
#  #  #  #  #
#############
```
Permutações

a) Faça uma função que receba como parâmetros uma matriz quadrada de largura $n$ e dois inteiros $i,j$. A função deve trocar os conteúdos das linhas $i$ e $j$ desta matriz entre si. Esta é uma operação de matrizes conhecida como permutação de linhas.

b) A matriz identidade $I$ é uma matriz quadrada cujos elementos da diagonal valem $1$ e os demais valem $0$. Assim, multiplicando-se $I \times A$, obtemos a própria matriz $A$. Modifique a matriz $I$ de forma a obter uma matriz $P$ tal que $P \times A$ é a matriz $A$ com as linhas $i$ e $j$ trocadas.

c) De maneira geral, uma matriz $P$ quadrada que só contém $0$ e $1$ tal que cada linha ou coluna só contenha um elemento não nulo é chamada de matriz de permutação. Crie uma função que receba $P$ e $A$ e calcule o produto $P \times A$. Use o fato de que $P$ é matriz de permutação para evitar fazer calculo de somas e produtos.

Exercícios criativos

Os gifs animados fizeram a alegria do início da Web e voltaram a fazer sucesso nos dias de hoje! Na sua forma mais simples, os gifs são uma sequência imagens bitmaps. Vamos implementar um efeito de máscara sobre um gif.

a) Descreva uma estrutura para representar um gif.

b) Escreva uma função que leia um gif do teclado (número de imagens, largura e altura e sequência de pixels de cada imagem) devolva um ponteiro para um gif alocado dinamicamente.

c) Escreva uma função para liberar a memória alocada para um gif.

d) Escreva uma função que receba uma imagem e uma máscara (imagem binária em branco e preto do mesmo tamanho) e aplique a máscara na imagem. A imagem deve ser alterada para manter apenas a parte correspondente aos pixels brancos da máscara, como no exemplo.

e) Escreva uma função para aplicar uma máscara em um gif.

Um desafio: Um quadrado latino de ordem $n$ é uma matriz em que cada elemento é um número de $1$ até $n$ e cada número aparece no máximo uma vez por linha e no máximo uma vez por coluna.

10     1     9     2     8     3     7     4     6     5
 7     8     6     9     5    10     4     1     3     2
 9    10     8     1     7     2     6     3     5     4
 5     6     4     7     3     8     2     9     1    10
 1     2    10     3     9     4     8     5     7     6
 2     3     1     4    10     5     9     6     8     7
 8     9     7    10     6     1     5     2     4     3
 3     4     2     5     1     6    10     7     9     8
 4     5     3     6     2     7     1     8    10     9
 6     7     5     8     4     9     3    10     2     1

a) É fácil verificar se uma matriz é um quadrado latino. O que parece não ser tão fácil é construir um quadrado latino. Faça uma função que receba uma inteiro $n$ e devolva um quadrado latino de tamanho $n \times n$.

b) Uma vez que você obteve um quadrado latino, encontrar outro é bem mais fácil. Faça uma função que receba uma matriz quadrada $n \times n$ totalmente preenchida com zeros, com exceção de duas posições. Essas posições foram copiadas de algum quadrado latino. Seu desafio é descobrir algum quadrado latino que tenha respeite essas posições. Por exemplo, se a entrada for a matriz

 0     0     0     0     0     0     0     0     0     0
 0     0     0     0     0     0     0     0     0     0
 0     0     0     0     0     0     0     0     0     0
 0     0     0     0     0     0     0     0     0     0
 0     0     0     0     0     0     0     0     0     0
 0     0     0     0     0     0     0     0     0     0
 0     0     0     0     0     0     0     2     0     0
 0     0     0     0     0     0     0     0     0     0
 0     0     0     6     0     0     0     0     0     0
 0     0     0     0     0     0     0     0     0     0

então uma resposta válida poderia ser o quadrado latino dado acima, já que ele respeita os valores 2 e 6 das posições não nulas. Qualquer outro quadrado latino com esses valores nessas posições também é permitido como saída.