Eficiência e tratabilidade de problemas

1. Vocês decidiram fazer uma festa surpresa para uma amigo hoje à noite. Para isso, você precisa cortar papel colorido e produzir bastante confete. Cada folha de papel deve ser cortada em 32 linhas e 32 colunas. Um amigo emprestou-lhe uma guilhotina e aconselhou: o melhor jeito de cortar o papel é enrolar uma folha e ir fazendo fitas, depois é só cortar cada uma das fitas separadamente.

   a) Descreva o procedimento sugerido como um algoritmo.

   b) Se você precisar cortar 100 folhas e gastar um segundo por cada corte da guilhotina, então quanto tempo levará para terminar a tarefa?

   c) Concorde ou discorde: embora esse algoritmo possa demorar horas, isso não significa que o problema não é viável, pois pode haver algoritmos mais espertos para a tarefa. Justifique.

2. Em um problema de calcular a potência à potência, temos:

   Entrada: número inteiro $k \ge 1$

   Saída: $2^{2^k}$

   Algoritmo 1:

   1. $p \gets 1$
   2. faça $k$ vezes:
      • $p \gets 2*p$
   3. $r \gets 1$
   4. faça $p$ vezes:
      • $r \gets 2*r$
   5. devolva $r$

   Algoritmo 2:

   1. $r \gets 2$
   2. faça $k$ vezes:
      • $r \gets r*r$
   3. devolva $r$

   Concorde ou discorde, justificando sua posição.

   a) O segundo algoritmo é mais rápido porque tem menos passos.

   b) O segundo algoritmo é mais rápido quando assumimos que cada instrução elementar gasta o mesmo tempo.

3. Uma maneira de tornar algoritmos mais eficientes é reaproveitando valores que já foram calculados anteriormente. Escreva um programa que imprima os $n$ primeiras somas parciais da série

   $$ \sum_{i=1}^n \left( (-2)^{n+i} + \frac{1}{2^i} \right). $$

   a) Faça uma versão que computa a $k$-ésima soma parcial fazendo uma chamada a uma função soma_parcial(i).

   b) Faça uma versão que reaproveita o valor da soma parcial computado anteriormente.

   c) Conte o número de multiplicações e somas que seu programa faz.

4. Uma máquina de troco (change-machine) é um equipamento comum em certos lugares, onde só se aceitam moedas. O objetivo é inserir uma ou mais cédulas e obter o valor equivalente no menor número de moedas. Suponha que a máquina possua um total de $N$ moedas para cada valor 1,00, 0,50, 0,25 e 0,10. Uma maneira de resolver o problema é testar todas as combinações possíveis de moedas, verificar quais correspondem ao valor inserido em cédulas e memorizar a de menor número de moedas. Naturalmente o número de combinações é muito grande. Calcule o número de combinações possíveis de moedas e argumente que esse algoritmo não é eficiente. Você é capaz de propor um algoritmo melhor?

Buscas

1. Se $L$ é uma lista de tamanho 8 e queremos encontrar um valor $k$ nessa lista, no pior caso, uma busca sequencial acessará a lista 8 vezes, mas a busca binária acessará apenas 4. Isso ocorre pois para uma lista ordenada de tamanho $n$, a busca sequencial acessa a lista até $n$ vezes, enquanto a busca binária realiza cerca de $\log_{2}(n)$ iterações. Sabendo disso, calcule o número de acessos no pior caso para um vetor de tamanho 16 e dê um exemplo de lista ordenada em que esse pior caso acontece.

2. Para uma lista não-ordenada, o que é mais vantajoso: uma busca sequencial ou ordenar e realizar busca binária? Explique.

3. Refaça a função de busca binária estudada. Dessa vez, suponha que a lista pode conter chaves repetidas.

   a) Implemente um versão, chamada busca_esquerda em que, se a chave aparecer mais de uma vez, devolve a primeira posição da lista de entrada que contém a chave.

   b) Faça uma versão busca_direita, que devolve a última posição.

4. Considere o seguinte problema: Temos como entrada uma lista de inteiros $v$ não necessariamente ordenada e um inteiro $x$. Desenvolva um algoritmo que determina se há dois números em $v$ cuja soma seja $x$. Tente fazer o algoritmo mais eficiente possível.

Exercícios criativos

1. Você irá escrever um programa interativo. Suponha que você recebe uma lista de números fracionários. Uma vez recebida essa lista, o usuário pode fazer uma série de consultas, que você deve responder usando funções mais rápidas que conseguir. Para isso, você pode preprocessar a sua lista antes mesmo que o usuário começar a fazer consultas. Assim, além da lista e dos dados da consulta, cada função recebe um parâmetro com os dados preprocesesados.

   a) Escreva uma função que conte quantos números da lista estão no intervalo $[a, b)$.

   b) Escreva uma função que calcule a média de todos os números que estão no intervalo $[a, b)$.

2. Suponha que você tem uma lista de inteiros L. Essa lista não está ordenada, mas você sabe que o primeiro elemento é negativo e que o último é positivo. Mais do que isso, você sabe que a diferença entre dois valores consecutivos é de no máximo um. Assim, se L[i] = 3, então L[i+1] deve valer 2, 3 ou 4. Escreva um algoritmo eficiente para encontrar a posição do zero nessa lista.

3. Em uma avenida central, há diversas ruas que a cruzam de maneira perpendicular, como na figura.

   

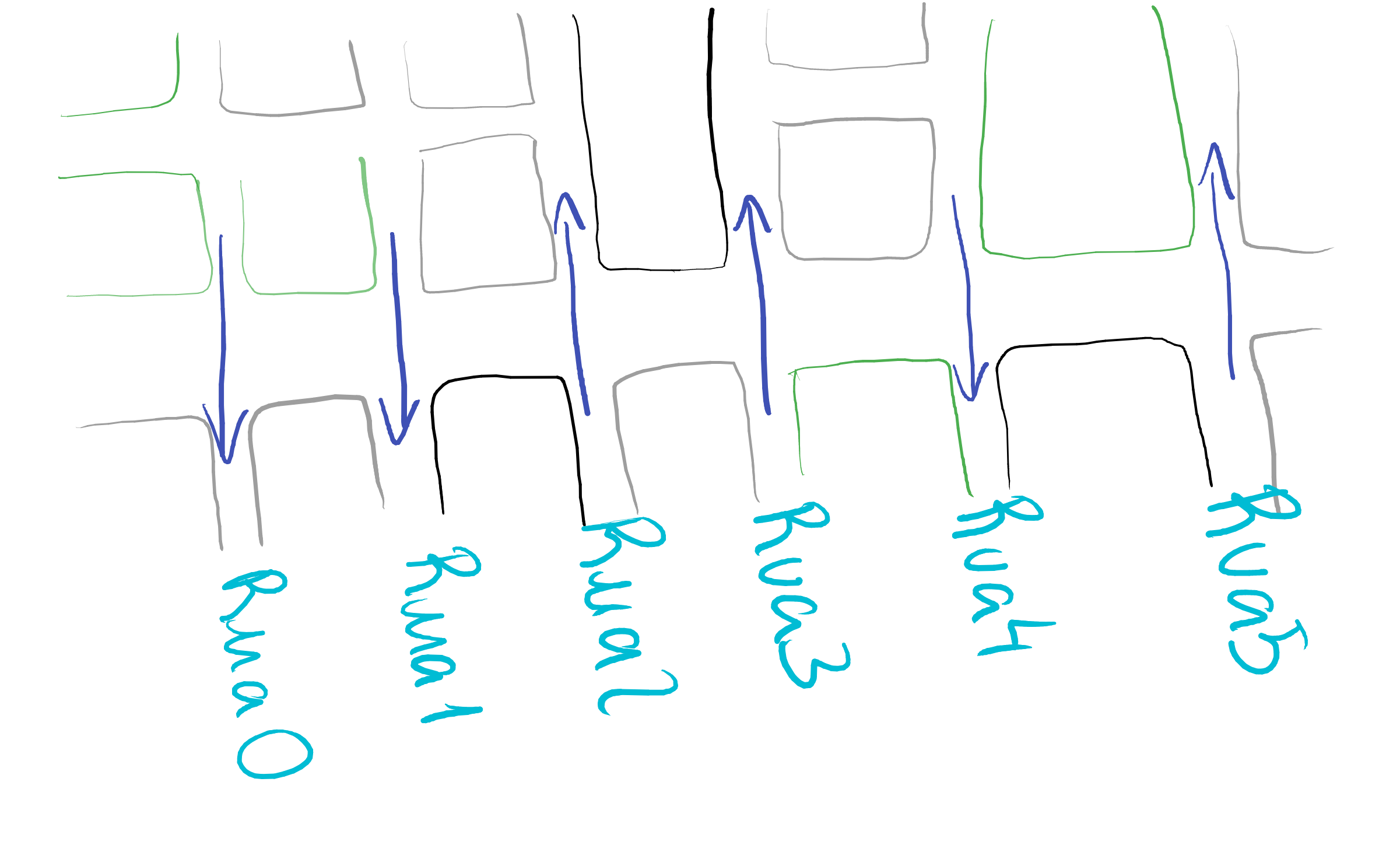
   Se você prestar atenção no sentido da primeira rua, verá que ele é para baixo enquanto o sentido da última rua é para cima. Suponha que esses sentidos são representados por um vetor de strings, como o exemplo para a figura acima.

   sentido = [ 'baixo', 'baixo', 'cima', 'cima', 'baixo', 'cima']
   

   Escreva um algoritmo que encontre eficientemente um par de ruas adjacentes com sentidos para baixo e para cima, respectivamente.