Nesta tarefa, vamos retornar ao tema ASCII ART para exercitarmos recursão. A inspiração para o nosso estudo será o Triângulo de Sierpinski. Ao analisarmos a figura abaixo, fica bem fácil entender o processo de criação deste fractal. A cada passo, um triângulo preto é substituído por três triângulos pretos menores, posicionados em forma de pirâmide. Os novos triângulos pretos serão subdivididos da mesma maneira no passo seguinte. O número de passos é, teoricamente, infinito.

O Triângulo de Sierpinski com ASCII ART foi o tema da tarefa sobre recursão do semestre passado. Neste semestre, iremos trabalhar com a mesma ideia, mas fazendo o desenho com quadrados de acordo com o modelo abaixo. Note que, a cada passo, um quadrado preto é substituído por três quadrados menores em forma de pirâmide.
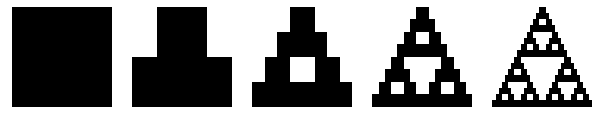
Quadrado base: O desenho é formado a partir de um quadrado inicial, pintado de preto no desenho original. Em ASCII ART, utilizaremos algum caractere para substituir a cor preta. Para facilitar a divisão da figura ao longo dos passos, trabalharemos apenas com quadrados cuja altura seja uma potência de 2 (altura = 2N).
altura = 20 |
altura = 21 |
altura = 22 |
altura = 23 |
|
|
|
|
Tela e moldura: Os desenhos deverão ser preparados em uma matriz de caracteres, denominada tela, e depois escritos na saída. A tela deverá ser uma matriz quadrada com as mesmas dimensões do quadrado base. Ao escrever a matriz, você deverá acrescentar um contorno de caracteres em branco e uma moldura feita com caracteres "-", "|" e "+", como no exemplo abaixo:
+----------+
| |
| @@ |
| @@ |
| @@@@ |
| @@@@ |
| @@ @@ |
| @@ @@ |
| @@@@@@@@ |
| @@@@@@@@ |
| |
+----------+
Profundidade da recursão: Em um fractal, não há limites para as subdivisões. Nesta tarefa, indicaremos o número de subdivisões, que deve ser sempre menor que valor de log2(altura), sendo altura a altura do quadrado base.
altura = 25 |
altura = 25 |
altura = 25 |
altura = 25 |
altura = 25 |
|
|
|
|
|
A entrada será formada por três valores:
<N>
<p>
<char_preto>
A altura do quadrado base e da tela será definida por 2N. O inteiro p indicará o número de subdivisões e o caractere <char_preto> indicará o caractere que preencherá o quadrado base.
A saída será formada por uma única tela
quadrada, com lado igual a p passos da
abordagem explicada neste enunciado.
O conjunto de testes será formado por 7 testes
abertos. Consulte o testes e resultados no
link Testes
para a tarefa 14 de mc102 ou no
arquivo aux14.zip. Haverá
mais 3 testes fechados, que são variações dos testes abertos em que só
foram alterados os caracteres utilizados para desenho.
Releia, se necessário, as instruções para fazer os testes em Testes com o SuSy.
Esta tarefa ficará simples de ser implementada se você subdividí-la em problemas menores, que devem ser desenvolvidos e testados separadamente. Veja a sugestão abaixo:
Desenvolva uma função para criar a tela com o caractere de preenchimento char_preto. Você pode usar o comando:
tela = [ [char_preto for j in range(largura)] for i in range(altura)]
Desenvolva uma função print_tela_com_moldura() para escrever esta tela com a moldura solicitada na saída.
Desenvolva uma função que desenha a
subdivisão de um quadrado preto a partir das
coordenadas x,y na tela. Teste a saída
com a função print_tela_com_moldura().
Desenvolva uma função que desenha, de forma
recursiva, o desenho solicitado nesta tarefa. Produza a saída com
a função print_tela_com_moldura().
Durante o desenvolvimento, acrescente chamadas extras à
função print_tela_com_moldura() de maneira que você
possa acompanhar o caminho que está sendo percorrido. Observe os
primeiros desenhos para N = 4, p = 3, char_preto =
"+" em que começamos a subdivisão pela esquerda:
+------------------+
| |
| ++++++++ |
| ++++++++ |
| ++++++++ |
| ++++++++ |
| ++++++++ |
| ++++++++ |
| ++++++++ |
| ++++++++ |
| ++++++++++++++++ |
| ++++++++++++++++ |
| ++++++++++++++++ |
| ++++++++++++++++ |
| ++++++++++++++++ |
| ++++++++++++++++ |
| ++++++++++++++++ |
| ++++++++++++++++ |
| |
+------------------+
+------------------+
| |
| ++++++++ |
| ++++++++ |
| ++++++++ |
| ++++++++ |
| ++++++++ |
| ++++++++ |
| ++++++++ |
| ++++++++ |
| ++++ ++++++++ |
| ++++ ++++++++ |
| ++++ ++++++++ |
| ++++ ++++++++ |
| ++++++++++++++++ |
| ++++++++++++++++ |
| ++++++++++++++++ |
| ++++++++++++++++ |
| |
+------------------+
+------------------+
| |
| ++++++++ |
| ++++++++ |
| ++++++++ |
| ++++++++ |
| ++++++++ |
| ++++++++ |
| ++++++++ |
| ++++++++ |
| ++++ ++++++++ |
| ++++ ++++++++ |
| ++++ ++++++++ |
| ++++ ++++++++ |
| ++ ++++++++++++ |
| ++ ++++++++++++ |
| ++++++++++++++++ |
| ++++++++++++++++ |
| |
+------------------+
Veja aqui a
página de submissão da tarefa. O arquivo a ser
submetido deve se chamar lab14.py. No
link Arquivos
auxiliares há um
arquivo aux14.zip que
contém todos os arquivos de testes abertos e seus respectivos
resultados compactados.
O limite máximo será de 30 submissões. Serão considerados os resultados da última submissão.
O peso desta tarefa é 3.
O prazo final para submissão é 12/07/2020.
A nota desta tarefa é proporcional ao número de testes que executaram corretamente, desde que o código esteja coerente com o enunciado. A submissão de um código que não implementa o algoritmo requisitado, mas que exibe as saídas esperadas dos testes abertos a partir da comparação de trechos da entrada será considerada fraude e acarretará a atribuição de nota zero à média final da disciplina.
As imagens que ilustram os passos do algoritmo de Sierpinski foram obtidas a partir do verberte referente ao Triângulo de Sierpinski na Wikipedia. Todos os outros desenhos foram gerados por programas em Python.