
Ata de Aula: 06/11/2002
Redatora: Cândida Nunes da Silva
7.3 Planaridade, Colorações
e Ciclos
Definição: (Wagner) Uma coloração
de faces própria de um grafo plano 2-aresta-conexo é uma
atribuição de cores para suas faces de forma que faces cujas
fronteiras compartilhem uma aresta tenham cores distintas. Uma k-coloração
de faces (própria) é uma coloração de faces
que usa k cores distintas. Um grafo plano é k-face-colorável
se pode ter suas faces coloridas propriamente com no máximo k cores
distintas.
Comentário: (Meu, pensado agora) O conceito de coloração
de faces é definido apenas para grafos planos pois a descrição
de uma face de um grafo depende de sua imersão. (Meidanis) Além
disso, só é possível colorir propriamente as faces de
grafos 2-aresta-conexos, pois arestas de corte estão sempre na fronteira
de uma única face, a face externa (infinita).
Definição: (Wagner-Meidanis) Uma triangulação
é uma grafo plano simples e conexo tal que toda face (inclusive a externa)
é um triângulo, ou seja, possui comprimento 3.
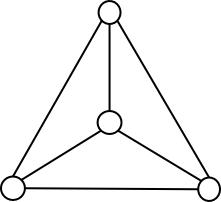
Exemplo: (Meu) Uma imersão no plano do tetraedro (K4),
ou do octaedro (mostradas abaixo) ou do icosaedro é uma triangulação.

|

|
Comentário: (João Guilherme-Meidanis) O grafo
dual de uma triangulação será sempre um grafo plano,
3-regular (cúbico) e 2-aresta-conexo. Nunca terá aresta de corte
pois esta representaria um laço no grafo original, que é simples.
Comentário: (Meidanis) k-colorir (propriamente) faces
de um grafo plano equivale a k-colorir vértices de seu dual. Para saber
se é possível k-colorir os vértices de qualquer grafo
plano, basta provarmos que é possível k-colorir as triangulações,
pois sempre é possível obter, a partir um grafo plano G, uma
triangulação T da qual G é subgrafo e, a partir de uma
k-coloração dos vértices de T, temos trivialmente uma
k-coloração dos vértices de G. Portanto, o teorema das
quatro cores se reduz para:
Teorema das 4 cores: É possível 4-colorir os vértices
de toda triangulação.
Ou, equivalentemente:
Teorema das 4 cores: É possível 4-colorir as faces
de todo grafo plano cúbico e 2-aresta-conexo.
O Teorema de Tait enunciado a seguir, mostrou que 4-colorir faces de um
grafo plano cúbico e 2-aresta-conexo é equivalente a 3-colorir
suas arestas. Este teorema trouxe uma nova abordagem para tentativas de demonstração
do teorema das 4 cores.
Teorema de Tait: (Cléber) Um grafo plano simples, cúbico
e 2-aresta-conexo é 3-aresta-colorável se, e somente se, for
4-face-colorável.
Definição: (Vinícius) Uma coloração
de Tait é uma 3-coloração própria de arestas
de um grafo cúbico.
Pergunta: (Meidanis) É sempre possível 3-colorir
as arestas de um grafo cúbico hamiltoniano?
Resposta: (Toda a turma) Sim. Todo grafo cúbico possui
um número par de vértices pois o grau de todo vértice
é ímpar e todo grafo possui um número par de vértices
de grau ímpar. Então o ciclo hamiltoniano é um ciclo
par e suas arestas podem ser coloridas com duas cores. As arestas ainda não
coloridas formam um emparelhamento perfeito, pois existe exatamente uma incidente
a cada vértice; portanto, estas podem ser coloridas com a terceira
cor de e o resultado é uma 3-coloração própria
das arestas do grafo.
Comentário: (Meidanis) Observando a existência
de 3-coloração de arestas para grafos cúbicos hamiltonianos,
Tait pensava ter provado o Teorema das 4 cores, pois acreditava ter provado
que todo grafo cúbico planar 2-aresta-conexo era hamiltoniano. No entanto,
anos mais tarde foi encontrada uma falha em sua demonstração
e, posteriormente, Tutte achou um contra-exemplo, um grafo cúbico planar
2-aresta-conexo não hamiltoniano. Esse contra-exemplo é apresentado
no livro, exemplo 7.3.6.
Definição: (João Paulo) Um snark
é um grafo cúbico, 2-aresta-conexo, com cintura pelo menos 5,
sem 3-corte não trivial e que não possui 3-coloração
de arestas.
Comentário: (Meidanis) Existem outros grafos cúbicos
além dos snarks que não contém 3-coloração
de arestas, mas estes sempre contém uma subdivisão de algum
snark.
Definição: (Raimundo) Um snark primo é
um snark que não contém uma subdivisão de um snark menor.
Comentário: A conjetura de Tutte sobre 3-coloração
de arestas enunciada a seguir e recentemente demonstrada implica que o grafo
de Petersen é o único snark primo.
Conjetura (agora Teorema) de Tutte: Todo grafo cúbico
sem arestas de corte que não é 3-aresta-colorável contém
uma subdivisão do grafo de Petersen.