Ata de Aula - 2002-11-13

Cap 8.2 [João Paulo] - Sistema Hereditário ou Família Hereditária é uma coleção de conjuntos F, tal que todo subconjunto de um conjunto em F está também em F.

[Luciano] Conjunto Independente: Conjunto da coleção F. Todo subconjunto dele é independente também.

[Luís Augusto] Bases: Conjuntos Independentes maximais.
Ex.: E = {a,b,c,x,y,z}
Independentes: Im = {a,b,c},{a,b},{a,c},{b,c},{a},{b},{c},{x,y},{x},{y},{}.
Bases: Bm = {a,b,c},{x,y}

[Raimundo] Circuito: Conjunto Dependente Minimal.
Ex.: Na coleção anterior: Cm = {z},{a,x},{b,y}

Posto de um subconjunto X de E é o tamanho máximo de um conjunto independente em X

[Silvia] Um Sistema Hereditário M em E é matróide se M satisfaz alguma das seguintes propriedades: Seja: I - conjuntos independentes;B - bases;C - circuitos;r - função posto de M.
I: "aumentação": Dados dois conjuntos independentes de tamanhos diferentes, o menor dos conjuntos mais algum elemento do maior conjunto é independente.
U: uniformidade: Para todo subconjunto de E, seus subconjuntos maximais independentes tem o mesmo tamanho.
B: Troca de Base: Dado um par de bases, para todo elemento presente na primeira base e não na segunda, existe um elemento presente na segunda e não na primeira, tal que a primeira base menos o primeiro elemento mais o segundo é uma base. Implica que tamanho das bases é sempre igual.
R: Submodularidade: A soma do posto da união com o posto da intersecção é menor ou igual a soma dos postos para todo par de subconjuntos de E.
A: Absorção fraca: Se o posto de um subconjunto de E é igual ao posto dele com um elemento a mais e é igual ao posto dele com outro elemento a mais, então o posto do subconjunto é igual ao posto do subconjunto com os dois elementos citados a mais, para todo subconjunto de E, e elementos pertencentes a E.
A': Absorção Forte: Se o posto de um subconjunto de E é igual ao posto deste subconjunto com qualquer elemento de outro subconjunto a mais, então o posto do primeiro subconjunto é igual ao posto da união dos dois subconjuntos.
C: eliminação fraca: Para todo elemento da intersecção de dois circuitos distintos, existe um outro circuito contido na união dos circuitos citados menos o elemento da intersecção.
J: circuitos induzidos: Um conjunto independente mais um elemento qualquer pode conter no máximo um circuito.
G: Algoritmo guloso: Para cada função não negativa em E, o algoritmo guloso gera um conjunto independente de peso total máximo.

Exemplo anterior [Luis Augusto] não é um matróide.

Matróide Ciclo: Matróide sobre E = conjunto das arestas de um grafo G cujos circuitos são os ciclos de G.

Matróide Gráfico: matróide que pode ser representado como o matróide clico de um grafo.

Matróide Vetorial: Matróide em que E representa vetores num espaço vetorial e F é formado pelos conjuntos de vetores linearmente independentes.

Matróide Linear: Matróide Vetorial.

Matróide Coluna: colunas de uma matriz A, vistas como vetores.

Matróide Transversal induzido pelos conjuntos A1,A2,...,Am, cuja união é E, é o Sistema Hereditário em E cujos conjuntos independentes são os sistemas de representantes distintos de {A1,A2,...,Am}.

Exemplo:

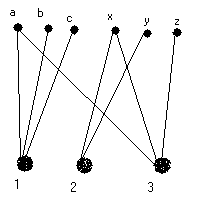
A1={a,b,c} A2={x,y} A3={a,x,z}
E={a,b,c,x,y,z}. E=U(Ai), 1<=i<=3.
Bases =
{ {a,x,z},{b,x,z},{c,x,z},
{a,y,z},{b,y,z},{c,y,z},
{b,x,a},{c,x,a},
{b,y,a},{c,y,a},
{a,y,x},{b,y,x},{c,y,x}
}

Alberto Miranda