MO405 - Exercícios - Propostos em 2002-08-28

Nos exercícios que perguntam "verdadeiro ou falso", deve-se justificar a resposta da seguinte forma: se for verdadeiro, com uma prova; se for falso, com um contra-exemplo.

1. (2.3.2 do livro) Verdadeiro ou Falso: Se T é uma árvore de peso mínimo de um grafo ponderado G, então o caminho u-v em T é o caminho u-v de menor peso em G.
2. (2.3.3 do livro) Existem cinco cidades em uma rede. O custo de construir uma estrada diretamente entre i e j é a entrada a_i,j da matriz abaixo. Uma entrada infinita (representada aqui pelo caracter '-') indica que há uma montanha no caminho e portanto a estrada não pode ser construida. Determina o menor custo de fazer com que todas as cidades sejam alcançaveis de qualquer outra.
   

   |  0 |  3 |  5 | 11 |  9 |
   |  3 |  0 |  3 |  9 |  8 |
   |  5 |  3 |  0 |  - | 10 |
   | 11 |  9 |  - |  0 |  7 |
   |  9 |  8 | 10 |  7 |  0 |
   

3. (2.3.5 do livro) Existem cinco cidades em uma rede. O tempo de viagem direto entre i e j é a entrada a_i,j na matriz abaixo. A matriz não é simétrica (use grafo orientado), e a_i,j='-' indica que não há uma rota direta. Determine o menor tempo de viagem e a melhor rota de i a j para todo par i,j.
   

   |  0 | 10 | 20 |  - | 17 |
   |  7 |  0 |  5 | 22 | 33 |
   | 14 | 13 |  0 | 15 | 27 |
   | 30 |  - | 17 |  0 | 10 |
   |  - | 15 | 12 |  8 |  0 |
   

Soluções - Discutidas em classe em 2002-09-04

1. 2.3.2

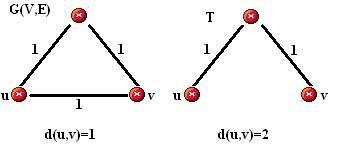
   Falso. Abaixo seguem o contra-exemplo apresentado em aula:
   

2. 2.3.3

   A árvore de custo mínimo obtida é a seguinte:
   
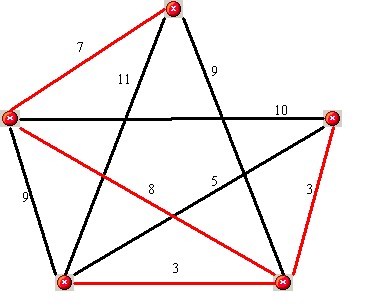
   Os passos da execução do algoritmo de Kruskal foram:

   Passo 1:	Escolha de uma aresta de menor custo do grafo (neste caso, A-B e B-C tem custo 3). Escolho A-B (3) para construir a árvore.
   Passo 2:	Escolha de uma aresta de menor custo do grafo. Escolho B-C (3) para construir a árvore.
   Passo 3:	Escolha de uma aresta de menor custo do grafo. Escolho C-A (5), porém C-A fecha um ciclo, sendo portanto, descartada.
   Passo 4:	Escolha de uma aresta de menor custo do grafo. Escolho D-E (7) para construir a árvore.
   Passo 5:	Escolha de uma aresta de menor custo do grafo. Escolho B-E (8) para construir a árvore.
   Passo 6:	N-1 arestas escolhidas. Fim do algoritmo.

3. 2.3.5

   Em sala, decidiu-se por exibir a solução do exercício a partir do vértice A. Os caminhos de menor custo obtidos foram:

     A->B    (custo=10)
     A->B->C (custo=15)
     A->E    (custo=17)
     A->E->D (custo=25)
   

   Os passos realizados pelo algoritmo de Dijkstra foram:

   Passo	A	B	C	D	E
   1 - Cálculo da distância a partir do vértice A	0(a)	10(a)	20(a)		17(a)
   2 - Vértice B escolhido.	0(a)	10(a)	15(b)	32(b)	17(a)
   3 - Vértice C escolhido.	0(a)	10(a)	15(b)	30(c)	17(a)
   4 - Vértice E escolhido.	0(a)	10(a)	15(b)	25(e)	17(a)
   5 - Todos os vértices alcançados. Fim do Algoritmo.	0(a)	10(a)	15(b)	25(e)	17(a)

   * Na matriz acima, 17(b) significa que o custo para se chegar no vértice em questão foi 17 e o último vértice do caminho desse custo foi 'b'.
   ** Em vermelho, destaque para os valores que mudaram em cada passo.
   *** Em azul, destaque para os vértices cujo caminho de menor custo já foi atingido.