MO405 - Exercícios -
Propostos em 2002-09-18
- (3.3.1 do livro)
- (3.3.2 do livro)
- (3.3.5
do livro)
- (3.3.6
do livro) – não foi resolvido na sala de aula no dia 23/09/2002
Soluções
- Discutidas em classe em 2002-09-23
- 3.3.1 Determine
se o grafo G abaixo tem 1-fator:
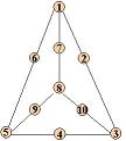
Seja S um conjunto de vértices, S = {1,3,5,8}. Então
o(G – S) = 6, onde componentes ímpares de G-S={2}, {4}, {6}, {7}, {9}, {10}.
Pelo Teorema de Tutte, um grafo G tem 1-fator <=>
o número de componentes ímpares de G-S, para qualquer S de G, deve ser menor ou
igual o número de vértices de S.
Assim, como existe pelo menos um S tal que isto não é
verdade, então G não tem 1-fator.
- 3.3.2 Exiba um emparelhamento máximo no grafo abaixo e utilize um resultado desta
seção (3.3) para mostrar um pequena prova de que não existe emparelhamento
maior:
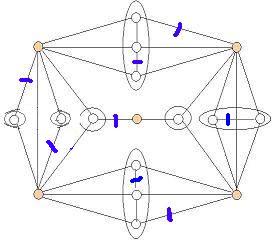
Escolhendo um conjunto de vértices S com 5 vértices preenchidos
(na figura acima), tem-se 7 componentes ímpares (circuladas na figura acima).
Assim, pelo Teorema de Tutte não existe emparelhamento
perfeito, porque o(T-S) > |S|.
Como o grafo tem 16 vértices, o emparelhamento perfeito
teria 9 arestas. Como o grafo não tem emparelhamento perfeito, o emparelhamento
ilustrado na figura é máximo.
- 3.3.5 Dado grafos
G e H, determine o número de componentes e o grau máximo de G v H em
termos dos parâmetros de H.
Número de componentes = 1.
Grau máximo = máx (grau máximo de G + |V(H)|, grau máximo
de H + |V(G)|).
- 3.3.6 Prove que
uma árvore T tem um emparelhamento perfeito se e somente se o(T-v)=1
para cada v pertencente a T.
Não foi resolvido em sala de aula no dia 23/09.