MO405 - Exercícios - Propostos em 2002-09-23

Nos exercícios que perguntam "verdadeiro ou falso", deve-se justificar a resposta da seguinte forma: se for verdadeiro, com uma prova; se for falso, com um contra-exemplo.

1. (4.1.1 do livro)
2. (4.1.7 do livro)

Soluções - Discutidas em classe em 2002-09-25

1. 4.1.1 Dê uma prova ou um contra-exemplo para cada uma das afirmações abaixo.

   a) Todo grafo com conectividade 4 é 2-conexo.

   Sílvia: Verdadeiro, pela definição. Se um grafo tem conectividade 4, então ele é 4-conexo, 3-conexo, 2-conexo e 1-conexo.

    

   b) Todo grafo 3-conexo tem conectividade 3.

   Vagner: Falso. Contra exemplo: grafo K_4,4, que tem conectividade igual a 4 e é 3-conexo.

    

   c) Todo grafo k-conexo é k-aresta-conexo

   Victor: Verdadeiro, para k >= 1. Pelo teorema de Whitney, a conectividade por arestas de um grafo é maior ou igual que a conectividade do grafo.

    

   d) Todo grafo k-aresta-conexo é k-conexo.

   Vinícius: Falso. Contra exemplo: grafo a seguir, que é 2-aresta-conexo mas não é 2-conexo.

   

    

2. 4.1.7 Obtenha uma fórmula para o número de árvores geradoras de um grafo conexo em termos dos números de árvores geradoras de seus blocos.

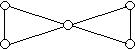
   Alberto: a fórmula é o produto dos números de árvores geradoras de cada bloco. Como os blocos do grafo só têm em comum um vértice, as árvores geradoras de um bloco não influenciam as árvores dos outros. Logo, o problema pode ser dividido e o nº total de árvores será o produto dos números das árvores dos blocos.

3. 3.3.6. Prove que uma árvore T tem um emparelhamento perfeito se e somente se o(T – v) = 1 para todo v Î V(T).

   Meidanis:

   Dados:

   • T é uma árvore
   • o(T - v) = 1 para todo v Î T.
   • |V(T)| = n
   • n é par, pois se não fosse, o(T - v) = 1 não ocorreria

    

   Provar: T tem um 1-fator

   A indução será feita sobre o número de vértices do grafo.

    

   Base: n = 2

   Neste caso só existe uma árvore, formada por apenas uma aresta. Nela, verifica-se o(T – v) = 1 para todo v, e possui um 1-fator.

    

   n >= 4

   Seja f uma folha de T.

   Seja g o único vértice adjacente a f em T.

   Sejam {f}, T₁, T₂, ..., T_k as componentes conexas de T – g.

   Seja t_i o vértice de T_i adjacente a g.

   

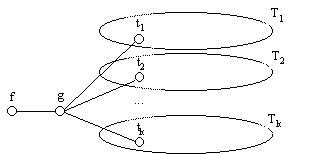
   Como o(T – v) = 1 e {f} é ímpar, temos que |V(T_i)| é par para 1 <= i <= k. Além disso, |V(T_i)| < n.

   É verdadeiro que o(T_i – v) = 1 para todo v Î V(T_i)? Se sim, a indução pode ser aplicada. Vamos verificar isto. Existem dois casos.

    

   Caso 1: v ¹ t_i

   Considere que as componentes de T_i – v são:

   C₁, C₂, ..., C_l

   sendo que t_i Î V(C₁).

   Ora, neste caso, as componentes de T – v são:

   C₁ U (T – T_i), C₂, ..., C_l

   C₁ U (T – T_i) é par. Ou seja, o(T_i – v) = o(T – v) = 1.

   Caso 1 ok!

    

   Caso 2: calcular o(T_i – t_i)

   Considere que as componentes de T_i – t_i são

   C₁, C₂, ..., C_l’

   Neste caso, as componentes conexas de T – t_i são:

   T – t_i, C₁, C₂, ..., C_l’

   T – t_i é par. Ou seja, o(T_i – t_i) = o(T – t_i) = 1.

   Concluímos que o(T_i – v) = 1 para todo v Î V(T_i).

    

   Por hipótese de indução, cada T_i tem um 1-fator F_i. Então T possui um 1-fator F₁ U F₂ U ... U F_k U {fg}