Exercicios da seção 5.2

Redador : Luís Augusto Angelotti Meira

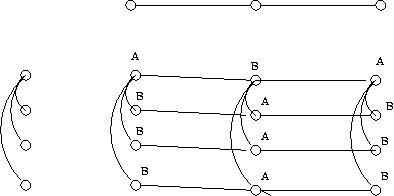
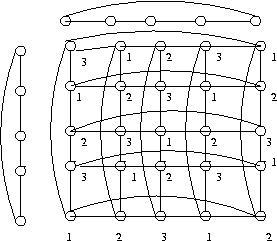
(5.1.9) Desenho o grafo K1,3 [] P3 e exiba uma coloração otima para ele. Desenhe C5[]C5 e encontre uma 3 coloração própria com tamanho das classes igual a 9,8,8

(5.1.12) Prove ou disprove: Cada grafo G k-cromático tem uma coloração própria de tamanho k na qual alguma classe de cor tem \alpha(G) vértices.
Falso.
Observe o grafo abaixo.

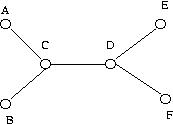
Neste grafo, que é 2 cromático, não existe coloração própria de tamanho dois que gere uma classe de tamanho 4.

( 5.2.5) Encontre uma subdivisão de K4 no grafo de Grotzsch.

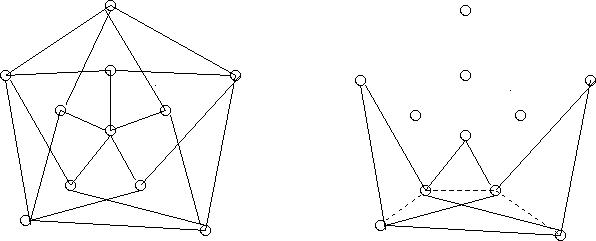
O desenha à direita representa um subgrafo do grafo de Grotszch. Este subgrafo é uma subdivisão de K4. Basta pensar que cada uma das aretsas tracejadas (que não existem na verdade) foi subdividida para obter um caminho de comprimento 2 (acima delas).