MO405 - Exercícios - Propostos em 2002-10-14

Seção 5.3 - Enumerative Aspects

Propostos em 14/10/2002.
Resolvidos em 16/10/2002.

Autor da ata: Vinicius José Fortuna

5.3.1 - Calcule os polinômios cromáticos dos grafos abaixo

Cláudio:
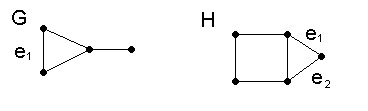
c(G ; k) = c(G - e₁ ; k) - c(G · e₁ ; k)
G - e₁ e G · e₁ são árvores, então podemos aplicar a fórmula de árvores:
c(G ; k) = k(k - 1)³ - k(k - 1)² = k(k - 1)²(k - 2) = k⁴ - 4 k³ + 5 k² - 2 k

Gilberto:

c(H ; k) = c(H - e₁ ; k) - c(H · e₁ ; k) = c(H' ; k) - c(C₄ ; k)

c(H' ; k) = c(H' - e₂ ; k) - c(H' · e₂ ; k)
c(H' ; k) = c(C₄ + v ; k) - c(C₄ ; k) = k c(C₄ ; k) - c(C₄ ; k)
c(H' ; k) = (k - 1) c(C₄ ; k)

c(H ; k) = (k - 1) c(C₄ ; k) - c(C₄ ; k) = (k - 2) c(C₄ ; k)

No exemplo 5.3.7 do livro temos c(C₄ ; k) = k (k - 1) (k² - 3 k + 3), então:

c(H ; k) = k (k - 1) (k - 2) (k² - 3 k + 3)

5.3.3 - Prove que k⁴ - 4k³ + 3k² não é um polinômio cromático.

Janaína:
Chamaremos tal polinômio de p(k). Fazendo k = 2 temos:
p(2) = 2⁴ - 4.2³ + 3.2² = 16 - 32 + 12 = -4
Absurdo, pois o polinômio cromático representa quantas formas pode ser pintado o grafo com k cores, o que deve ser um número inteiro não negativo.
Portanto p(k) não é um polinômio cromático.

Observações

c é a letra minúscula grega "chi"

· é um ponto à meia altura