MO405 - Exercícios - Propostos em 2002-10-21

Soluções - Discutidas em classe em 2002-10-23

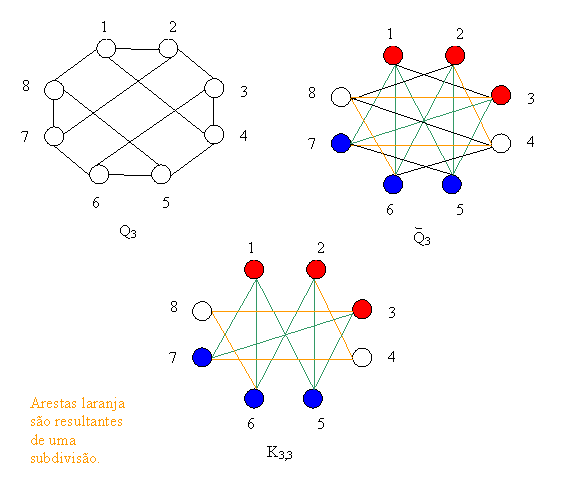
6.2.1 Prove que o complemento de um cubo de 3 dimensões Q₃ é não planar.

Solução: Encontrar uma sub-divisão de K_3,3 no complemento de Q₃. (Diogo)

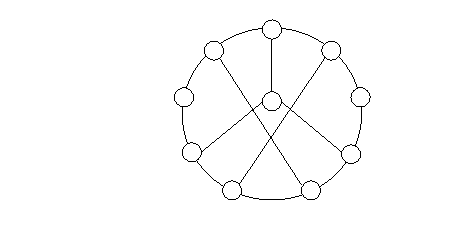
6.2.2 Dê três provas de que o grafo de Petersen é não planar.

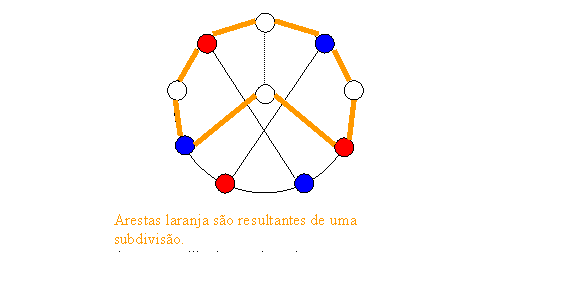
a) Usando o Teorema de Kuratowski. (Evandro)

b) Usando a Fórmula de Euler e o fato de que o grafo de Petersen tem cintura 5. (Gilberto)

Se P é Planar, então

n –e + f = 2

10 -15 + f = 2

f = 7

Pela proposição 6.1.13, 2e(G) = ∑ l(F_i), onde l(F_i) é o comprimento da face i de um grafo planar.

Dado que a cintura do grafo é 5 e f =7, aplicando-se a proposição acima, temos

f * 5 <= 2e(G)

7 * 5 <= 2e(G)

e>= 17,5

Assim, há uma contradição. Logo, o grafo de Petersen não é planar.