MO405 - Solução dos Exercícios
propostos em 2002-10-23
resolvidos em 2002-10-28

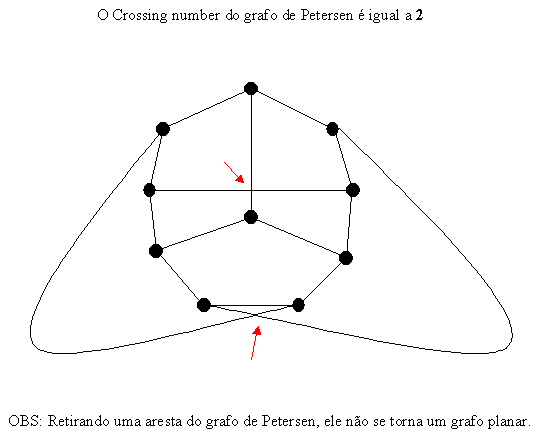
6.3.4 Determine o crossing number dos grafos: K2,2,2,2,  K4,4  e grafo de Petersen.

  Como a cintura é 5, as faces deveriam ter, no mínimo, 5 arestas cada uma.

  n = 10

  n - e + f = 2    =>   f = 2 - n + e

 5f <= 2e

 f <= 2e/5         =>   2 - n + e <= 2e/5

                               10 - 5n + 5e <= 2e

                               3e <= 5n - 10

Para justificar que o crossing number não pode ser menor, considere o argumento abaixo. Seja g a cintura de um grafo. Podemos obter o seguinte limite superior do número de arestas para o grafo ser planar:

2e >= g (2 - n + e)

2e >= 2g - gn + ge

ge - gn + 2g <= 2e

e (g - 2) <= g (n - 2)

e <= ( g(n - 2)) / g - 2

No caso de qualquer subgrafo gerador do K2,2,2,2 temos n = 8 e g pelo menos 3, logo

e <= 18

Como K2,2,2,2 tem 24 arestas, e um subgrafo seu gerador planar tem no maximo 18 arestas, conclui-se que o crossing number é no mínimo 6.

Novamente,

2e >= g (2 - n + e)

2e >= 2g - gn + ge

ge - gn + 2g <= 2e

e (g - 2) <= g (n - 2)

e <= ( g(n - 2)) / g - 2

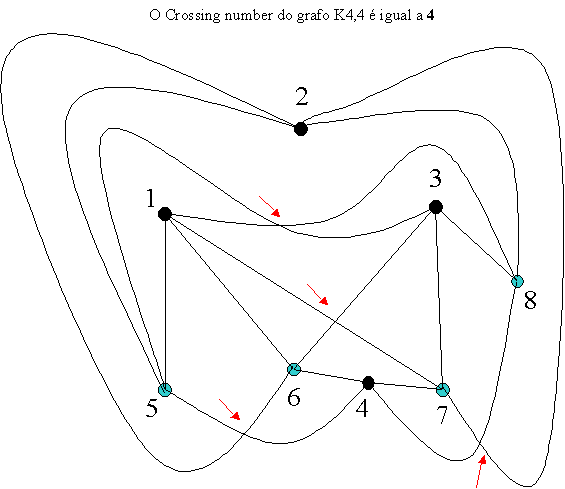
No caso de qualquer subgrafo gerador do K4,4 temos n = 8 e g pelo menos 4, logo

e <= 12

Como K4,4 tem 16 arestas, e um subgrafo seu gerador planar tem no maximo 12 arestas, conclui-se que o crossing number é no mínimo 4.

6.3.5 Prove que todo grafo planar G se decompõe em dois grafos bipartidos.

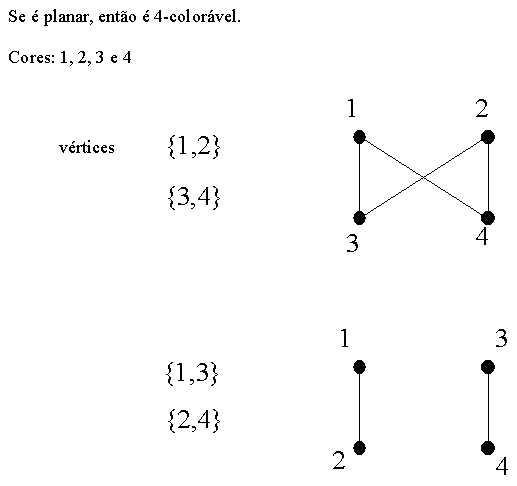
Coloque de um lado todas as arestas do tipo 13,14,23 e 24. De outro lado, as aretas do tipo 12 e 34. Cada lado gera um subgrafo de G. Estes sub grafos são bipartidos e formam uma decompisição do grafo G.

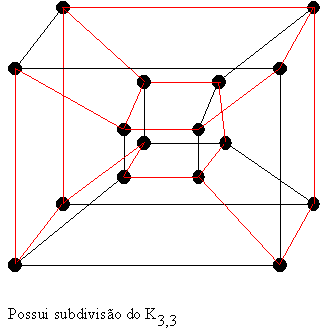
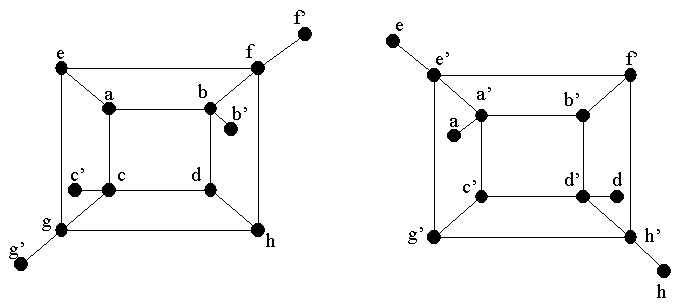
6.3.16 Prove que cubo Q4 4-dimensional não é planar. Decomponha-o em dois grafos planares isomorfos; portanto Q4 possui espessura 2.