7.1.1
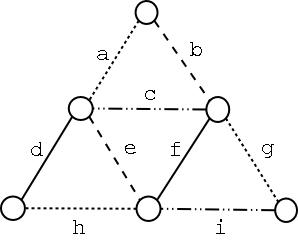
Para cada um dos grafos a seguir, compute seu índice cromático
e desenhe seu grafo linha.
Solução:
Dada pelas figuras abaixo. As arestas com diferentes padrões
representam as cores utilizadas para colorir as arestas de cada grafo e
as letras identificam as arestas do grafo e os respectivos vértices
do grafo linha.
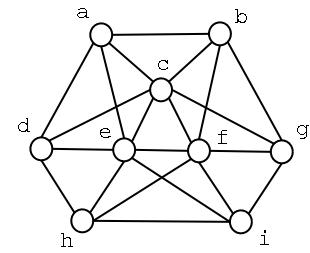
Grafo 1: Índice cromático
4, o grafo é classe 1. Uma 4-coloração das arestas
é apresentada à esquerda e o grafo linha é apresentado
à direita . (Cláudio)
|

|

|
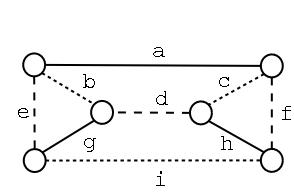
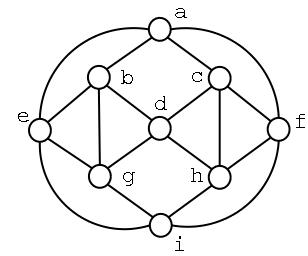
Grafo 2: Índice cromático
3, o grafo é classe 1. Uma 3-coloração das arestas
é apresentada à esquerda e o grafo linha é apresentado
à direita . (Cleber)
|
|
|
7.1.1 Dê uma coloração
de arestas explícita para provar que o número cromático
de Q_k é igual ao seu grau máximo (k).
Solução: (Desirée)
Basta colorir com cor i as arestas que ligam vértices que representam
os números binários com apenas o i-ésimo bit da representação
distinto. Como cada vértice representa um número de k bits,
k cores são suficientes.
Podemos demonstrar que essa
coloração existe por indução:
Base: k=1. Basta
atribuir a cor 1 à única aresta de Q_1 que liga os dois
únicos vértices que representam os diferentes bits.
Hipótese: É
possível obter uma (k-1)-coloração das arestas de Q_k-1
tal que uma aresta de cor i liga apenas vértices que representam
números binários com apenas o bit i distinto.
Passo: O
grafo Q_k pode ser decomposto em dois Q_k-1 mais um emparelhamento perfeito
M. Sejam v_1, v_2, ..., v_2^(k-1) e v_1', v_2', ..., v_2^(k-1)'
os vértices de cada um dos Q_k-1 e (v_i, v_i'), para
1<= i <= 2^(k-1) as arestas de M, sendo que os números
binários representados por v_i e v_i' diferem apenas no k-ésimo
bit.
Por hipótese de indução, é
possível obter uma (k-1)-coloração das arestas de Q_k-1
tal que uma aresta de cor i liga apenas vértices que representam
números binários com apenas o bit i distinto. Então,
basta atribuir a cor k às arestas do emparelhamento M para obtermos
uma k-coloração das arestas de Q_k
tal que uma aresta de cor i liga apenas vértices que representam
números binários com apenas o bit i distinto.
CQD.