7.2.7
Um rato come um cubo de 3x3x3 de queijo comendo todo os subcubos de 1x1x1durante seu caminho. Se ele comeca num subcubo de canto e sempre se move para um subcubo adjacente (que divide uma face de area 1), o rato pode fazer isto e comer o subcubo do centro por último? De um método ou prove que é impossível. (Ignore a gravidade.)
Solução:
Este cubo pode ser visto como um grafo onde os vertices são os subcubos
de tamanho 1, e arestas ligam os subcubos que dividem uma face de área 1.
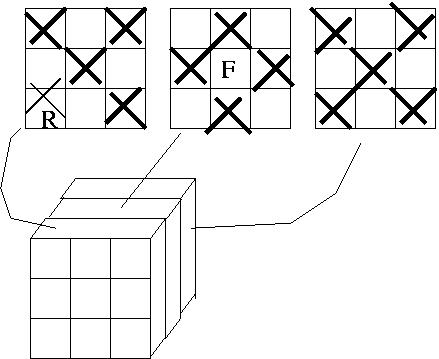
Este é um grafo bipartido.Representando o cubo por 3 quadrados de 3x3, respectivamente o quadrado
da frente, o do meio e o do fundo, podemos ver claramente a bipartição:

O rato começa em uma partição e deve terminar em outra, portanto ele deve percorrer um numero ímpar de arestas. Para comer todos os vértices (de queijo), o rato deve andar um caminho com 3³ vértices, ou seja um P_27. O número de arestas de P_27 é 26, portanto todo caminho que o rato faça percorrerá um número par de arestas. Sendo assim, é ímpossível o rato comer todos os subcubos e terminar no subcubo central.
7.2.8 Em um tabuleiro de xadrez, um cavalo pode
mover de uma casa que difira de 1 em uma coordenada e de 2 em outra, como
mostrado no livro (pag. 295). Prove que nenhum tabuleiro de tamanho 4xn tem um
ciclo hamiltoniano do cavalo: uma sequencia de movimentos de cavalo que
passa por todos os vértices e termina no inicial. (Dica: ache um conjunto apropriado de vertices que viole a condição necessária.)
Solução:
Modela-se este problema para um grafo com os vértices representando as
casas do tabuleiro, e as arestas ligando casas que podem ser alcançadas
com um movimento de cavalo. Para existir um ciclo hamiltoniano do cavalo, é preciso que este grafo tenha ciclo hamiltoniano. Verificaremos que a
condição seguinte é violada para todo tabuleiro 4xn:
7.2.3 (livro) Se G tem um ciclo hamiltoniano, então para cada conjunto não
vazio de vértices S contido em V(G), o grafo G-S tem no máximo |S| componentes.
Seja S o conjunto dos vértices equivalentes as casas pretas das duas
linhas do meio do tabuleiro 4xn, representadas em preto na figura. As casas
logo acima das casas em preto na linha de cima e as casas logo abaixo das
casas em preto na linha de baixo em vermelho são vértices
desconexos em G-S, representados em vermelho, os vértices restantes, mostrados em branco, formam outra componente. Como o número
de vértices sem vizinhos é igual a n, e há mais uma componente, temos n+1
componentes em G-S, como |S| = n, este grafo viola a condição, portanto não é possível achar um ciclo hamiltoniano do cavalo.
