MO405 - Exercícios - Propostos em 2002-11-11

Seção 8.1 - Perfect Graphs

Propostos em 11/11/2002.
Resolvidos em 13/11/2002.

Autor da ata: Ulisses Furquim Freire da Silva

8.1.1 - Calcule chi(G) e omega(G) para o complemento do ciclo ímpar C_2k+1.

Prova:
Lembrando que alpha(G) é igual ao omega(complemento(G)) e que alpha(C_2k+1) = k, prova-se que omega(complemento(C_2k+1)) = k.

Usando mais uma vez que alpha(G) é igual ao omega(complemento(G)), sabemos que omega(C_2k+1) = 2, então alpha(complemento(C_2k+1)) = 2. Assim, chi(complemento(C_2k+1)) >= teto(n/alpha) = teto((2k+1)/2) = k+1. Basta mostrarmos que conseguimos colorir propriamente o complemento de C_2k+1 com k+1 cores. Começando no vértice 1, podemos colorir com a mesma cor dois vértices consecutivos. Dessa maneira, damos a cor 1 para os vértices 1 e 2, a cor 2 para os vértices 3 e 4, e assim por diante, até colorirmos com a cor k os vértices 2k-1 e 2k. O vértice 0 não poderá ter nenhuma das k cores já utilizadas, pois terá arestas para vértices coloridos com todas as k cores. Assim, colorimos o vértice 0 com a cor k+1, o que acaba de provar que chi(complemento(C_2k+1)) = k+1.

8.1.2 - Determine o menor grafo imperfeito G tal que chi(G) = omega(G).

Resposta:
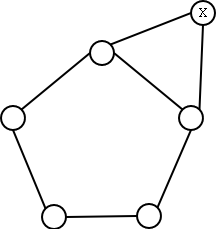
O grafo G abaixo tem chi(G) = omega(G) = 3. Retirando-se o vértice X ficamos com o C₅, que possui chi(C₅) = 3 e omega(C₅) = 2. Assim, prova-se que o grafo G é imperfeito. O grafo G é provavelmente o menor imperfeito com chi(G) = omega(G), pois o C₅ é o menor imperfeito, e G tem o mínimo de vértices e arestas a mais que o C₅. Note que C₅ mais uma corda é perfeito, e que C₅ mais um vértice e uma aresta apenas também é perfeito.