8.3.15 – Verifique que R(p,2) = R(2,p) = p. Use isto e o Teorema 8.3.11 para provar que R(p,q) <= C_{p+q-2, p-1}

Resolução:

1ª parte: R(p,2) = R(2,p) = p

Para mostrar isso, mostramos que R(p,2) >= p e R(p,2) <= p.

Para uma clique de tamanho p-1 R(p,2) >= p

Agora provamos por indução que R(p,2) <= p

Base: R(1,2) = 1(trivial)

Hipótese de indução: R(p-1,2) = p-1

Passo indutivo: R(p,2) <= R(p-1,2) + R(p,1)(Teorema 8.3.11)

R(p,2) <= p-1 + 1(Pela hipótese de indução)

R(p,2) <= p

Portanto: R(p,2) = R(2,p) = p

2ª parte: R(p,q) <= C_{p+q-2, p-1}

Com resultado obtido na primeira parte da resolução podemos construir a seguinte tabela para os valores de R(p,q)
 

p\q	1	2	3	4	5	6
1	1	1	1	1	1	1
2	1	2	3	4	5	6
3	1	3
4	1	4
5	1	5
6	1	6

 

Preenchendo os valores em branco com a soma R(p-1,q) + R(p,q-1)(limite superior de R(p,q) dado pelo teorema 8.3.11) temos:
 
 
 

p\q	1	2	3	4	5	6
1	1	1	1	1	1	1
2	1	2	3	4	5	6
3	1	3	6	10	15	21
4	1	4	10	20	35	56
5	1	5	15	35	70	126
6	1	6	21	56	126	252

Tomando-se as “diagonais secundárias” da tabela, obtemos o Triângulo de Pascal. Pela propriedade do Triângulo de Pascal temos: R(p,q) <= C_{p+q-2, p-1}

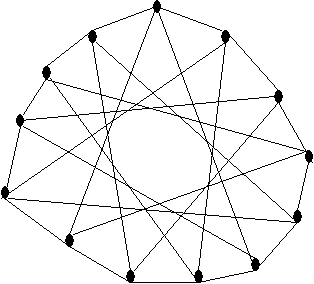
8.3.16 – Use o grafo abaixo para provar que R(3,5) = 14

Resolução:

Pelo Teorema 8.3.11 temos:

R(3,5) <= R(3,4) + R(2,5)

R(3,5) <= 9+5

R(3,5) <= 14

Resta então mostrar que R(3,5) >= 14 utilizando o grafo dado na questão.

Pela construção do grafo, observa-se que os vértices adjacentes a um determinado v não são adjacentes a nenhum vizinho de v. Portanto não existem cliques de tamanho 3 (triângulos).

Pegando-se 2 vértices de distância 2 e tirando-se seus vizinhos e adjacentes, sobra apenas um subgrafo com 4 vértices cujo conjunto independente tem tamanho 3. Então ao todo o conjunto independente do grafo tem tamanho no máximo 4. Como o grafo não possui clique de tamanho 3 nem conjunto independente de tamanho 5 e possui 13 vértices, então R(3,5) >= 14.

Logo R(3,5) = 14.

8.3.39 – Compute as larguras de banda de P_n, K_n, e C_n

Resolução:

B(P_n)= 1

B(K_n)= n-1

B(C_n)= 2