Exercícios          (02/12/2002)

8.3.15 – Esperança

a)      Compute o número esperado de pontos fixos em uma permutação aleatória de [n].

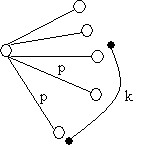
b)      Determine o número esperado de vértices de grau k em um grafo aleatório  com n vértices com probabilidade p para a existência de uma aresta.

Resolução:

a) Seja X_i uma variável aleatória tal que X_i = 1 se i está na posição certa e X_i = 0 se i está na posição errada.

E(X_i) = Pr( i estar na posição certa) = 1/n

Seja X = Número de pontos fixos = Somatório(X_i) para i variando de 1 até n.

Portanto,

            E(X) = E(Somatório(X_i) para i variando de 1 até n)

            E(X) = Somatório(E(X_i)) para i variando de 1 até n      (pela linearidade da esperança)

                E(X) = n * (1/n) = 1

b) A idéia é calcular a probabilidade de um vértice v fixo ter grau k. Seja X_v uma variável aleatória tal que X_v = 1 se v tem grau k, e 0 caso contrário. Somando-se todos os E(X_v) chega-se à esperança desejada.

  E(X_v) = Pr( v ter grau k)

O vértice v possui n-1 potenciais vizinhos, dentre os quais escolhe-se k.

Portanto a probabilidade de v ter grau k é dada por:

Pr(v tem grau k) = E(X_v) = p^k * (1-p)^n-1-k * C_n-1,k             

Logo, o número esperado de vértices com grau k é

E(X) = E(Somatório(X_v) para todo v)

E(X) = Somatório(E(X_v)) para todo v (pela linearidade da esperança)

E(X) = n * p^k * (1-p)^n-1-k * C_n-1,k 

8.5.3 – Determine o número esperado de triângulos monocromáticos em uma 2-coloração aleatória de E(K₆)

Resolução:

Como o grafo é completo, quaisquer 3 vértices formam um triângulo. Portanto devemos ver qual o número de triângulos existentes no total e quantos deles são monocromáticos.

O número de total de triângulos é dado por C_6,3 = 20

A probabilidade de um triângulo ser monocromático pode ser calculada da seguinte forma:

A primeira aresta escolhida para o triângulo pode ser de qualquer cor. A probabilidade de a segunda e a terceira arestas serem da mesma cor que a primeira é 1/2. Portanto, a probabilidade de o triângulo ser monocromático é 1/2 * 1/2 = 1/4.

Logo,

E(X) = 20 * 1/4 = 5.

8.5.10 – Seja G um emparelhamento de tamanho n. Escolha uma conjunto de k vértices aleatoriamente. Calcule o número esperado de arestas induzidas pelos vértices selecionados.

Resolução:

Para uma aresta ser induzida, seus 2 extremos devem ser selecionados.

A probabilidade de selecionar o primeiro vértice é k/2n

A probabilidade de selecionar o segundo vértice é (k-1)/(2n-1)

Seja X_i a variável que diz se uma aresta é induzida, então

P(X_i) = (k/2n) * (k-1)/(2n-1)

Logo, E(X_i) = p(X_i = 1) = (k/2n) * (k-1)/(2n-1)

E(X) = E(Somatório(X_i) para i variando de 1 até n)

E(X) = Somatório(E(X_i)) para i variando de 1 até n

E(X) = n * ((k*(k-1))/(2n*(2n-1)))

E(X) = (k*(k-1))/(2*(2n-1))