MO417 - Atas das Aulas

Assunto: Capítulo 6 - Heapsort

Ata da aula: 12/02/2003
Redator: André Santanchè

Tópicos:

Heaps: heap mínimo, heap máximo;
MAX-HEAPIFY;
BUILD-MAX-HEAP;
Heapsort e seu invariante;
HEAP-MAXIMUM, HEAP-EXTRACT-MAX, HEAP-INCREASE-KEY, MAX-HEAP-INSERT

Heaps: heap mínimo, heap máximo

O Heap pode ser visto como uma árvore binária praticamente completa (semi-completa), cujo comportamento é caracterizado conforme um de seus dois tipos:

Heap máximo: dado qualquer nó da árvore que possua filhos, o valor deste nó sempre será maior ou igual ao valor dos seus nós filhos.
Heap mínimo: dado qualquer nó da árvore que possua filhos, o valor deste nó sempre será menor ou igual ao valor dos seus nós filhos.

Representação do heap em um vetor

Para representar o heap de modo linear em um vetor, utilizam-se as seguintes relações:

Dado um nó na posição i no vetor (posições começam em 1):

A posição de seu nó pai é sempre o piso da metade de i.
A posição de seu filho da esquerda, se existir, é sempre duas vezes i.
A posição de seu filho da direita, se existir, é sempre duas vezes i mais um.

Pode-se observar que como as ligações entre pais e filhos são feitas através de relações de posição em um vetor, isto exige uma estrutura que permita um acesso direto a cada posição. Isto torna este tipo de organização de heap inadequada a uma lista encadeada, por exemplo.

MAX-HEAPIFY

Em primeiro lugar qual o objetivo da sub-rotina MAX-HEAPIFY?

Ela é responsável por manter a propriedade do heap, ou seja, dado qualquer nó, raiz de um heap, seu valor deve ser maior que o valor de seus filhos.

Para isto o MAX-HEAPIFY executa uma arrumação:

Inicialmente analisamos apenas o nível dos filhos imediatamente abaixo da raiz do heap, conforme o seguinte exemplo:

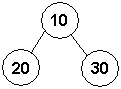
Note que a disposição dos valores nos nós não está atendendo a propriedade do heap, ou seja, o valor do pai (10) é inferior ao valor de ambos os filhos.
Neste caso o nó que possui maior valor (30) troca com o pai.

O procedimento pára neste nível?
Não. Para se garantir a propriedade do heap é necessário que ela seja válida para todos os níveis abaixo.
Quando ocorre uma troca, para ajuste do heap, apenas um dos filhos é afetado. No exemplo apresentado, apenas o lado do filho direito foi afetado. Deste modo, a sub-rotina MAX-HEAPIFY executa uma chamada recursiva a si mesma, para ordenar a sub-árvore (sub-heap) cuja raiz foi modificada. No exemplo apresentado será para a sub-árvore da direita.

É importante destacar algumas características do comportamento de MAX-HEAPIFY:

Ele arruma um caminho da árvore de heap, a partir de uma posição que é informada como parâmetro.
Por se tratar de uma árvore binária quase completa, a cada deslocamento que a sub-rotina executa para uma sub-árvore, obteremos aproximadamente a metade dos elementos. Por este motivo o tempo de execução no pior caso será O(lg n).

BUILD-MAX-HEAP

A sub-rotina BUILD-MAX-HEAP constrói um heap máximo de acordo com os seguintes passos:

Inicialmente considera que cada folha da árvore de heap principal a ser construído já é um heap, uma vez que as folhas não possuem filhos, atendendo necessariamente à propriedade do heap.
O algoritmo começa processando o nó na posição piso(n/2), pois este é o primeiro nó do heap (partindo-se dos níveis mais baixos para os mais altos, da direita para a esquerda) que possui algum filho e que pode não atender à propriedade do heap.
A partir desta posição inicial (piso(n/2)), a repetição for do BUILD-MAX-HEAP aplica para cada nó (indicado pelo índice do for) o MAX-HEAPIFY. O índice do for vai decrementando, o que equivale a percorrer o vetor da direita para a esquerda e a árvore de baixo para cima.

Qual a complexidade deste algoritmo?

Inicialmente se supõe que seja O(n lg n), dado que o MAX-HEAPIFY executa em tempo O(lg n) e o BUILD-MAX-HEAP executa aproximadamente n/2 iterações.

Uma análise mais detalhada demonstra que na árvore do heap existem no máximo teto(n/2^h+1) nós raízes de sub-árvores de altura h. Como a alturas das sub-árvores na árvore principal variam entre 0 e piso(lg n) e o tempo que MAX-HEAPIFY processa um heap de altura h é O(h), o custo total para processar o heap completo será de:

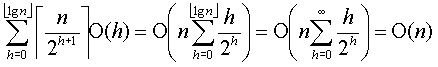
Intuitivamente podemos entender este resultado percebendo que, na medida que nos deslocamos da raiz para as folhas, o número de nós aumenta, mas inversamente, o tempo demandado para o processamento de cada nó diminui.

O artifício de transformar o somatório de [0 a lg n] para [0 a infinito] foi utilizado pois, deste modo, pode-se facilmente calcular o resultado que será um valor constante (2). Como o segundo somatório é necessariamente maior que o primeiro a propriedade O se mantém.

O cálculo do número de sub-árvores de altura h pode ser entendido intuitivamente da seguinte maneira: na medida que nos deslocamos da raiz da árvore principal para as folhas, o número de sub-árvores dobra (exceto no último nível) e a altura diminui de um, ou seja, precisamos de uma equação que aumente o número de sub-árvores em uma proporção inversa a redução da altura destas sub-árvores em uma potência de dois.

Heapsort e seu invariante

O Heapsort completo funciona da seguinte maneira:

Inicialmente é acionada a sub-rotina BUILD-MAX-HEAP para construir um heap do vetor inteiro. Em seguida inicia-se um processo de ordenação baseada no heap, que repete as seguintes etapas para todos os elementos do vetor, iniciando-se do último e indo em direção ao segundo:

Troca o último elemento do heap com o primeiro.
O novo último elemento fará parte do vetor ordenado, portanto deve sair do heap, deste modo o tamanho do heap diminui de um.
Como o primeiro elemento (trocado) provavelmente não atende às propriedades do heap, o MAX-HEAPIFY é acionado para reordenar o heap a partir da raiz modificada.

O tempo de execução do Heapsort é O(n lg n) pois, como foi demonstrado, o tempo de execução do BUILD-MAX-HEAP é O(n), adicionalmente o do MAX-HEAPIFY é O(lg n), mas ele é chamado n-1 vezes, o que torna todo o processo O(n lg n).

Duas coisas interessantes podem ser observadas neste processo de ordenação:

Quanto temos um heap montado em um vetor A, qualquer sub-vetor de A cujo início coincida com o início de A, também é um heap.
A construção do vetor final ordenado a partir do heap é feita de trás para frente.

Loop Invariante do Heapsort

O Loop Invariante é dado no exercício 6.4-2:

HEAPSORT(A)
1 BUILD-MAX-HEAP(A)
2 for i <- comprimento[A] downto 2
3    do trocar A[1] <-> A[i]
4      tamanho-do-heap[A] <- tamanho-do-heap[A]-1
5      MAX-HEAPIFY(A, 1)
No início de cada iteração do loop for das linhas 2 a 5, o subarranjo A[1..i] é um heap máximo contendo os i menores elementos A[1..n], e o subarranjo A[i+1..n] contém os n-i maiores elementos de A[1..n], ordenados.

Intuitivamente pode-se compreender este invariante percebendo-se que para cada valor de i do loop for, ele determina que todos os elementos do início do vetor até a posição i ainda fazem parte de um heap (com os menores elementos) e todos os elementos de posição acima de i já fazem parte de um vetor ordenado com os maiores elementos.

Este invariante é verdadeiro antes da primeira iteração do loop (inicialização) pois i é igual ao comprimento do vetor, deste modo, não há elementos com posição acima de i e todos os elementos até i fazem parte do heap recém construído.

O invariante é verdadeiro a cada iteração (manutenção), pois dentro do loop ele executa inicialmente a modificação de dois componentes o da posição 1 e o da posição i, trocando-os. O elemento da posição 1 é reordenado dentro do heap pelo MAX-HEAPIFY, garantindo que o heap se refaça até a posição i-1. O elemento da posição i, por sua vez, era anteriormente o maior do heap (raiz) que foi agora inserido no início da lista ordenada. Essa lista continuará ordenada dado que ela possui os maiores elementos de todo o vetor e agora recebe um valor que é por um lado o maior do heap e por outro menor que todos os elementos do vetor ordenado, assumindo sua posição exata no vetor ordenado final. Quando o loop fecha o laço, o i assume a próxima posição e a propriedade se verifica, dado que o heap (de um lado) e o vetor ordenado (de outro) se mantém corretamente.

Finalmente o invariante é verdadeiro no final (término) dado que o i estará na posição 1. Deste modo, o heap será de apenas um elemento e portanto está necessariamente correto, do outro lado todos os elementos acima da posição i estão ordenados e são os maiores.

O Heapsort realiza uma ordenação local, ao contrário do Mergesort que, para realizar a operação de Merge, necessita de espaço adicional fora do vetor, cujo tamanho não é constante.

O Heapsort é uma solução boa para registros de tamanho grande?

Nestes casos deve-se observar duas coisas:

É possível se separar a chave do restante do registro, mantendo-se sua ligação através de ponteiros. Deste modo, opera-se a ordenação com as chaves+ponteiros apenas.
Mesmo se for realizada a ordenação com um registro grande completo, ele tem um tamanho constante, portanto o tempo de ordenação será multiplicado por uma constante, o que não afeta sua complexidade.

HEAP-MAXIMUM, HEAP-EXTRACT-MAX, HEAP-INCREASE-KEY, MAX-HEAP-INSERT

Operações que se podem realizar com um heap quando este é utilizado em filas de prioridades:

Verificar o elemento máximo (HEAP-MAXIMUM): é simples e direto pois envolve apenas a consulta da raiz do heap.
Extrair o máximo (HEAP-EXTRACT-MAX): extrai-se o elemento da raiz (que é o máximo), coloca-se o elemento da última posição do heap na raiz (de onde foi retirado o máximo), diminui-se o tamanho do heap e utiliza-se o MAX-HEAPIFY para reposicionar o elemento da raiz, reordenando o heap.
Aumentar o valor de uma chave (HEAP-INCREASE-KEY): se a chave nova fornecida como parâmetro for maior do que a chave da posição indicada para incremento (i), substitui-se a chave. Além disto, nesse caso:

compara-se o nó i (incrementado) com seu pai, se ele for maior é realizada uma troca entre seus valores, isto implica que, em seguida, o índice i passará para a posição do pai e o processo descrito neste item se repete novamente, até que não haja mais troca ou que se alcance a raiz do heap.

Inserir um elemento (MAX-HEAP-INSERT): este procedimento no fundo é muito próximo ao HEAP-INCREASE-KEY. A diferença é que antes de executar o processo do HEAP-INCREASE-KEY, ele cria um espaço adicional no final do vetor do heap com valor menos-infinito e neste espaço executa o HEAP-INCREASE-KEY com a chave a ser inserida.

O autor (Thomas H. Cormen do livro Algoritmos) não apresenta um algoritmo para redução de chave (HEAP-DECREASE-KEY), mas é perfeitamente possível implementá-lo com eficiência, dado que, além do decremento da chave, o processo necessário para reordenação do heap será o MAX-HEAPIFY. Portanto é interessante acrescentar o HEAP-DECREASE-KEY como uma nova operação adicional para filas de prioridades.

Pode-se observar que a estrutura do heap é eficiente para algumas operações, tais como as apresentadas, mas não será para outras. Deste modo, é importante notar que cada estrutura é mais apta para um certo conjunto de operações.

O heap não é uma estrutura interessante para auxiliar em uma única operação de busca. Seu uso exigiria, para uma busca, a construção de um vetor ordenado, para posteriormente se realizar a busca. O processo total demandaria um tempo O(n lg n) que é pior do que o algoritmo de busca seqüencial, que possui tempo no pior caso O(n).