|
Elementos de programação dinâmica (Ricardo convidado a se expressar) |
O que um problema de otimização deve ter para que a programação dinâmica seja aplicável?
As duas principais características são subestrutura ótima e superposição de subproblemas.
Um problema apresenta uma subestrutura ótima quando uma solução ótima para o problema contém em seu interior soluções ótimas para subproblemas.
Uma forma padrão para descobrir uma subestrutura ótima é descrita em quatro passos:
| 1. |
Mostrar que a solução para o problema consiste em fazer uma escolha. Esta escolha
deixa um ou mais subproblemas a serem resolvidos. |
| 2. |
Supor que para um subproblema, sabe-se a escolha que leva a uma solução ótima. |
| 3. |
Dada esta escolha, determinar quais subproblemas resultam dela e como caracterizar
melhor o espaço de subproblemas resultante. |
| 4. | Mostrar que as soluções para os subproblemas usados dentro da solução ótima para o problema devem elas próprias ser ótimas. Por exemplo, por contradição: supondo que cada uma das soluções dos subproblemas, que formam a solução do problema, não é ótima. Neste caso, substituindo a solução do subproblema por uma solução ótima, contradiz a suposição, uma vez que uma solução melhor que a original é encontrada. |
|
Sutilezas (Tiago convidado a se expressar) |
Deve-se ter cuidado para não presumir que a subestrutura ótima está presente onde ela não está. A exemplo do problema de Caminho simples mais longo não-ponderado exposto no livro. O termo não-ponderado distingue o problema do "equivalente" para o caso do grafo ser ponderado. Indica que nenhum peso é atribuído às arestas do grafo. O termo simples indica que não há repetição de vértices no caminho.
A chave da questão é que os subproblemas do Caminho simples mais longo não-ponderado não são independentes. Isto significa que a solução para um subproblema pode afetar a solução para outro subproblema. Por outro lado, no caso do Caminho mais curto não-ponderado os pedaços (subproblemas) do caminho mais curto também são caminhos mais curtos, ilustrando a noção de subestrutura ótima, além de não interferirem nos outros subproblemas.
|
Número total de subproblemas a resolver (Eric e Daniele ausentes,
Nielsen convidado) |
O segundo principal indicativo para usar a programação dinâmica é a superposição de subproblemas. Acontece quando um algoritmo recursivo reexamina o mesmo problema muita vezes. No caso da multiplicação de matrizes, discutido na aula anterior, o algoritmo recursivo percorre O(2n) subproblemas, mas existem O(n2) subproblemas distintos. Então o número de subproblemas é uma função polinomial do tamanho da entrada, o que sugere que a programação dinâmica pode fornecer uma solução eficiente para o problema.
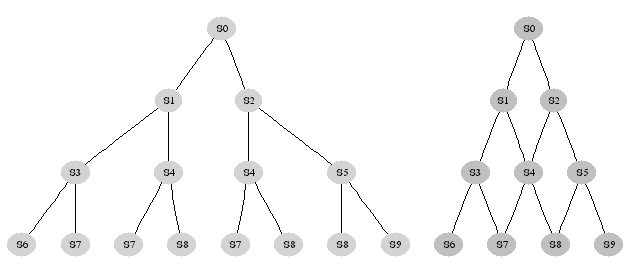
|
Ilustração do caminho percorrido por um algoritmo recursivo e por um de programação
dinâmica. Usando a programação dinâmica os subproblemas são avaliados
apenas uma vez. |
Para o caso de existirem muitos subproblemas que não necessitam ser resolvidos (caso lembrado por Nielsen), usar a estratégia de memoização (lembrada por André) pode ser mais eficiente. Ela consiste em usar o algoritmo recursivo natural para o problema, mas ao encontrar um subproblema pela primeira vez, este é resolvido e seu resultado armazenado em uma tabela para o caso de ocorrer novamente.
|
Subseqüência comum mais longa (Alexandro convidado a se expressar) |
Em aplicações biológicas para determinar o quão são "semelhantes" duas cadeias de DNA se busca uma subseqüência comum mais longa entre as duas. Intuitivamente uma subseqüência é uma seqüência obtida de outra ao se remover alguns elementos. Difere da noção de subcadeia pois seus elementos não precisam se encontrar imediatamente um após o outro na cadeia original. Uma seqüência é subseqüência dela mesma.
|
|
André - Como exatamente SCL é válido para comparação de DNA? Meidanis - Imagine que ontem eu estava convertendo uma apresentação de inglês para português. No primeiro slide, apaguei tudo e refiz. A partir do segundo, comecei a observar que muitas palavras podiam ser "aproveitadas". A exemplo de success → sucesso e productivity → produtividade. Comecei então uma divertida empreitada para tentar encontrar um número mínimo de operações que transformava o slide inteiro para português. Uma das razões por trás destas, não incomuns, ocorrências é que as palavras "evoluíram" de uma mesma língua. E o DNA não difere muito das palavras. Os organismos também "emprestam" muitas coisas: divisão celular, respiração. Muitas vezes queremos saber o quanto difere uma seqüência da outra ou quantas operações são necessárias para se transformar uma na outra. Eduardo - Por que não simplesmente ordenar o arquivo e resolver o problema em O(n lg n)? Meidanis - Porque não estaríamos procurando o SCL das cadeias originais, e sim de permutações das cadeias que na verdade não interessam. Obs: As palavras acima não são exatamente as que foram usadas pelas pessoas em questão. |
Seguem as quatro etapas para o desenvolvimento da solução por programação dinâmica (ver aula anterior):
Etapa 1 - Caracterização de uma subseqüência comum mais longa (Carlos convidado)
|
Dadas duas cadeias, X e Y, de comprimentos n e m,
respectivamente, considere os elementos terminais de cada uma, xn
e ym. a. Se ambos forem iguais, o elemento zk = xn = ym faz parte de uma SCL das cadeias. A cadeia formada dos elementos encontrados de forma semelhante, mas anteriores, a zk, Zk-1 é uma SCL das duas cadeias formadas pelos elementos que antecedem xn e ym, Xn-1 e Ym-1 respectivamente. Usamos a notação Xn-1 para designar a subcadeia de X que vai de 1 até n-1. b. Se forem diferentes, então implica que zk é diferente de xn ou ym, implica que Zk é uma SCL de Xn-1 e Ym ou Xn e Ym-1 respectivamente. |
Etapa 2 - Solução recursiva (Ivan convidado)
Com base na equação 15.14 encontrada no livro. Uma matriz C m+1 x n+1
é montada para X de tamanho m e Y de tamanho n. O
valor de C[i, j] indicará o comprimento da SCL para as
subcadeias Xi e Yj. O valor de C[i, j] para i=0 ou j=0 é 0, pois se trata
do caso trivial: comparação com pelo menos uma cadeia vazia. Para xi = yj,
C[i, j] = C[i-1, j-1] + 1, pois um novo elemento de uma
SCL foi encontrado. Caso xi ≠ yj, se mantem o maior tamanho
de SCL encontrado até então: C[i, j] = máx{C[i-1, j],
C[i, j-1]}.
| |||||||||||||||||||||||||||
Etapa 3 - Como calcular o comprimento de uma SCL (Augusto convidado)
|
O algoritmo recursivo precisaria resolver um número da ordem exponencial de subproblemas,
enquanto existe um número da ordem quadrática (tabela) de subproblemas. Há muita repetição. Algoritmo na página 283 do livro. |
Etapa 4 - A construção de uma SCL
| Para recuperar a seqüência que forma uma SCL: Começa do último quadrinho C[m, n], e verifica qual foi o anterior. Diagonal se C[i, j] = C[i-1, j-1] + 1, esquerda ou acima caso o valor da esquerda ou o de cima sejam maiores. Percorre-se a tabela desta forma gravando os valores das posições em que o anterior veio da diagonal. |
|
Árvore de busca ótima (Camila convidada a se expressar) |
O problema é montar uma árvore de busca ótima para acelerar a consulta de palavras. É dado um conjunto fixo de palavras, a probabilidade de ocorrência de cada uma (probabilidades das chaves reais), e as probabilidades de não ocorrência (probabilidades para as chaves fictícias). As chaves fictícias representam os valores de chaves que não se encontram na árvore.
Nesta situação a palavra mais freqüente não necessariamente é a que fica mais embaixo na árvore de busca. O problema consiste em minimizar a equação 15.16 (página 286 do livro).
Etapa 1 - A estrutura de uma árvore de busca ótima (Guilherme convidado)
|
Os subproblemas são trechos contínuos dos dois vetores de entrada. Semelhante ao
exemplo da multiplicação de matrizes (referência à aula anterior). A subárvore resultante vai ser solução ótima do subproblema. Pois considerando ótima a solução, caso o subproblema não seja ótimo, uma opção ótima poderia substituí-lo o que levaria a solução final a ser ainda melhor que a ótima, contrariando a hipótese. |
Etapa 2/3 (André convidado)
| À medida que vai "subindo" de subproblemas menores para subproblemas maiores, o algoritmo vai realizando uma soma cumulativa. É determinado onde cada subproblema começa e termina (i, j). A tabela gerada é da ordem de O(n2). O que o faz com que o problema seja perfeito para a programação dinâmica. |
|
| Disciplina: | MO417 - Complexidade de Algoritmos I |
| Livro texto: | Algoritmos : teoria e prática / Thomas H. Cormen... [et al.]; tradução da segunda edição [americana] - Rio de Janeiro : Campus, 2002 |
| Redator: | Bruno Cedraz Brandão 022245 |