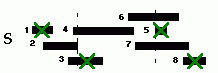Resumo
-
Os algoritmos gulosos são usados em alguns problemas onde podemos
também utilizar programação dinâmica, porém com um custo de execução
menor. Esses algoritmos utilizam alguma heurística para encontrar
a solução ótima. Normalmente se faz uma escolha que parece
ser ótima em determinado passo, e em uma análise top-down, vai se
resolvendo os subproblemas até que (como esperado) se cheque na solução
ótima global do problema. Por este motivo, nem todos os algoritmos onde
a programação dinâmica é aplicada, por compartilhar essa propriedade
de subestrutura ótima, uma estratégia gulosa pode ser utilizada. De fato,
só poderemos utilizar uma estratégia gulosa quando a partir de uma escolha
ótima local que fizermos, subdividirmos nosso problema em apenas um
subproblema a ser solucionado, não dependendo de outras escolhas ou da
solução de outros subproblemas. Além disso, deve existir um modo
de fazer esta escolha local que funcione.
1. Introdução
Uma breve descrição dos tópicos do capítulo 16 do livro do Cormen (2002) será apresentada nesta ata. Todos os tópicos aqui apresentados foram abordados durante a aula da disciplina Complexidade de Algoritmos ministrada no 1º semestre letivo de 2003 pelo professor João Meidanis, na data do dia 09 de abril de 2003, das 08:00 às 10:00.2. Algoritmos Gulosos
2.1. Visão Geral
- Os algoritmos
para problemas de otimização geralmente seguem uma sequência de passos, com
um conjunto de escolhas a cada passo. Os algoritmos gulosos sempre fazem uma
escolha que parece melhor em um determinado momento, o que significa dizer que
esses algoritmos fazem uma escolha local ótima na esperança dessa escolha
tender a uma solução global ótima. Discutiremos a seguir alguns problemas de
otimização que são resolvidos utilizando algoritmos gulosos, e como determinar
quanto podemos aplicar esta estratégia para encontrar uma solução para um
determinado problema de otimização.
- Prof. seleciona o colega Alexandro para enunciar o problema
de seleção de atividades (enunciado bem completo).
Colega Alexandro: Você tem um conjunto de atividades que
possuem um tempo de início e um tempo de término. Por exemplo, você
tem em um conjunto {a1, a2, ... an}.
Cada atividade ai dessas tem um tempo de início e de término.
Interrupção do prof. para um comentário: Por exemplo, começar as quatro horas da tarde (16:00) e terminar as cinco e meia (17:30). Os tempos são fixos.
Alexando continua: O que você tem que fazer? Você tem que encontrar um subconjunto dessas atividades, tal que cada elemento desse subconjunto não seja superposto a outro, i.e., o tempo de início de um elemento não seja menor que o tempo de término de um outro. A idéia é você pegar um subconjunto que tenha essa propriedade, e este subconjunto seja o maior, o maior subconjunto possível. Para que isso seria interessante? Você poderia ter um recurso que seria utilizado por este conjunto, e você queira utilizar o máximo de atividades para maximizar a utilização deste recurso. - Prof. complementa: Por exemplo, uma sala de conferência
ou uma sala de reuniões. Vários grupos querem usar a sala e cada um tem
uma necessidade.
Alexandro interrompe para comentar: Ou seja, você está privilegiando a quantidade.
Prof. continua: Você está privilegiando a quantidade! Eu vou alocar, alguns vão ficar sem, mas eu vou alocar o máximo possível. (Reforça)Você está privilegiando a quantidade!
2.2. Seleção de Atividades
- O problema de
Seleção de atividades consiste agendar a utilização de um determinado recurso
por um conjunto de atividades. Suponha que você tenha um conjunto
S = {a1, a2,..,an}
de n atividades propostas que desejam utilizar um mesmo recurso, tal como
uma sala de conferências, que pode ser utilizada por apenas uma atividade por um
determinado período de tempo. Cada atividade ai tem um tempo de
início si e um tempo de término fi, onde
si < fi. Duas atividades ai
e aj são compatíveis se os intervalos
[si, fi) e [sj, fj)
não se sobrepõem, i.e., se si >= fj ou se
sj >= fi. O problema de Seleção de
Atividades consiste em encontrar o subconjunto de tamanho máximo de atividades
mutuamente compatíveis.
Discussão em aula a respeito desse tópico:
- A atividade am está presente em um subconjunto Si,j de tamanho máximo de atividades mutuamente compatíveis
- O subproblema Si,m é vazio, de tal maneira que am deixa o subproblema Sm,j como o único que pode ser não vazio
- Prof. seleciona o colega Carlos e pergunta sobre o Teorema 16.1:
Talvez a gente precise de uns pré-requisitos pra falar sobre este teorema.
Carlos: Acho que precisa falar sobre a subestrutura ótima!
Prof. comenta: Então tudo bem, fale-nos sobre a subestrutura ótima.
Carlos: A subestrutura ótima é você ter um intervalo, ou melhor,
um intervalo onde o tempo de iníncio e término dela não sobreponha as atividades
anterior e posterior, pra você poder fazer recursivamente a união desses
intervalos para ter a solução ótima.
Prof. comenta: Vamos por parte. Eu achei que o teorema cita uma coisa chamada Si,j. Nós não sabemos o que é esse Si,j.
Carlos: Si,j é o subconjunto das atividades lógicas. A sequência ocupa o recurso.
Prof. pergunta: Que subconjunto?
Carlos: Subconjunto das atividades desse intervalo
Prof. pergunta: Que intervalo?
Carlos: Intervalo de i até j, que vai da atividade ai até a atividade aj.
Prof. comenta: Não sei se é bem isso. A atividade ai está, por exemplo, no conjunto Si j?
Carlos: É o subconjunto das atividade ai até a atividade aj que estão em sequência.
Alexandro comenta: Ou seja, depois que ai terminou.
Prof. comenta: Tem mais um problema aqui. Se nós comparamos números, eu entendo que você fale as palavras esse é menor que aquele e todos que estão entre esse e aquele. Porém, quando nós estamos falando de intervalos, nem sempre você pode falar que este esta antes daquele ou todos entre este e aquele. Intervalos não são comparáveis, porque cada intervalo tem um ponto de início e ponto de fim. O que você quer dizer quando você fala este antes daquele?
Carlos: O ponto final de um está antes do ponto inicial do seguinte, eles nunca se sobrepõem.
Prof. comenta: Mas na entrada, as atividades se sobrepõem.
Carlos: Mas este conjunto Si,j será um de tal forma que elas não se sobrepõem entre ai e aj.
Prof. comenta: Eu discordo de você. Si,j pode conter atividades que se sobrepõem sim.
Alexandro comenta novamente Só está limitando os extremos.
Prof. comenta: Só está limitando os extremos!
Augusto. comenta: As atividades são compativies com aj mas que podem não ser compatíveis com todas as atividades.
André. comenta: As atividades que começam depois ou igual ao fim de ai, e terminam antes ou igual ao início de aj.
Prof. solicita ao Carlos para ler a definição na página 297. Solicita que ele resuma em uma frase com menos de 10 palavras.
Carlos: Pelo que eu consigo entender aqui é que as atividades não estão se sobrepondo, elas são independentes.
Prof. comenta: Então vamos ter que fazer um desenho (levanta e vai até a lousa pra desenhar):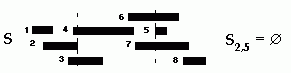
Fig. 1: Exemplo para seleção de atividades, Teorema 16.1.
- Prof. seleciona o colega Ivan e pergunta: Sabemos o que é o
problema e sabemos o que é Si,j, que é um subproblema. Pelo jeito,
este problema goza da propriedade da subestrutura ótima, para este tipo
de subproblema. Ou seja, se eu tenho uma solução para S, esta solução
contém uma solução para Si,j para todo i e j? Diga-nos
o que diz o teorema 16.1.
Ivan: Ele vai considerar uma atividade am tal que ela tenha o tempo de término mais antigo, i.e., ela termina primeiro dentro do subconjunto Si,j. Sobre esta condição podemos afirmar 2 fatos:
-
1º: Essa atividade vai estar no subconjunto Si,j;
2º: Sm,j != Ø.
André interrompe para comentar: Intuitivamente essa segunda dá pra entender, mas a prova dele eu não consegui entender mesmo tendo lido cerca de 3 vezes. Inclusive acho que tem um erro e até discordo de algumas coisas.
Prof. Comenta: Entendi o que ele quer fazer. Suponha que você tenha uma solução ótima. Ele quer tirar o primeiro cara dessa solução e colocar am no lugar. Ele deveria então ter definido A'i,j da forma:A'i,j = (Ai,j \ Ak) U {am} Deveria ser assim na minha opinião. Então o teorema fala o seguinte: Em qualquer subproblema não vazio da forma Si,j, você pega o cara que termina primeiro. Esse cara você pode tirar ele porque alguma solução ótima vai contê-lo. Isso imediatamente nos dá uma divisão do problema em 2 subproblemas. Quando escolho um cara e digo que ele vai estar na solução ótima, eu na verdade divido em 2 subproblemas: o que acontece antes dele e o que acontece depois dele. Neste caso, o que acontece antes dele não acontece nada. Isso nos dá uma idéia de como funciona o algoritmo guloso.
2.3. Teorema 16.1
-
Considere um subproblema não vazio Si,j, e seja am
uma atividade com o menor tempo de término:
A prova para este teorema está no livro texto.
Discussão em aula a respeito desse tópico:
2.4. Algoritmo guloso interativo
-
A seguir descrevemos um algoritmo guloso interativo para solucionar o problema
de seleção de atividades. No entanto, é assumido que o conjunto de atividades
fornecido como entrada esteja ordenado pelo tempo de término das atividades, i.e.,
da atividade mais antiga (a que termina primeiro) para a mais nova (última a
terminar).
Caso contrário, poderíamos então ordenar o conjunto de atividades pelo seu tempo de término, mas isso levaria O(n lg n).