MO417 - Ata de Aula - Heaps binomiais e de Fibonacci
Ata da aula do dia 23/04/2003
Redator: Alexandro José Baldassin - ra 022243
Tópicos:
1. Tabela da figura 19.1
2. Árvores binomiais
3. Definição de heap binomial
4. União de heaps binomiais
5. Definição de heaps de Fibonacci
1. Tabela da Figura 19.1
Essa tabela mostra o tempo de execução das operações
executadas em heaps binários (já estudados), binomiais e de
Fibonacci, e é apresentada logo abaixo.
Procedimento
|
Heap binário
(pior caso) |
Heap binomial
(pior caso) |
Heap de Fibonacci
(amortizado) |
| MAKE-HEAP |
Θ(1) |
Θ(1) |
Θ(1) |
| INSERT |
Θ(lgn) |
O(lgn) |
Θ(1) |
| MINIMUM |
Θ(1) |
O(lgn) |
Θ(1) |
| EXTRACT-MIN |
Θ(lgn) |
Θ(lgn) |
O(lgn) |
| UNION |
Θ(n) |
O(lgn) |
Θ(1) |
| DECREASE-KEY |
Θ(lgn) |
Θ(lgn) |
Θ(1) |
| DELETE |
Θ(lgn) |
Θ(lgn) |
O(lgn) |
Tabela 19.1 - tabela de complexidade das operações
sobre heaps binários, binomiais e de Fibonacci
Começamos analisando as operações referentes aos heaps
binários, pois quase todas já foram estudadas no capítulo
do livro referente ao Heapsort. A operação que foi analisada
com mais cuidado foi a de UNION, que é realizada fazendo-se a concatenação
de dois heaps binários e depois aplicando-se a operação
BUILD-MIN-HEAP (no caso de heap mínimo). Sua eficiência é
portanto Θ(n), já que o tempo de concatenação é
Θ(1) e o de BUILD-MIN-HEAP é Θ(n) (similar ao BUILD-MAX-HEAP
já visto no capítulo sobre Heapsort). Outra observação
feita foi que a operação MAKE-HEAP somente cria um novo heap
vazio, e portanto é Θ(1), diferente do BUILD-HEAP, que cria efetivamente
um heap (máximo ou mínimo), e é O(n) para o
binário.
Então passamos a comparar as operações
do heap binomial com as do heap binário. De imediato vimos que a operação
UNION é O(lgn) no caso binomial, contra O(n) no caso
binário. No entanto, MINIMUM é O(lgn) para o binomial
e Θ(1) para o binário. Portanto, se nossa aplicação
usar bastante a operação de MINIMUM, um heap binário
seria mais interessante do que um binomial. De modo similar, caso a operação
de UNION fosse a mais utilizada, daríamos preferência para o
heap binomial ao invés do binário.
Para terminar a análise da tabela, verificamos as
operações para o heap de Fibonacci. A primeira impressão
foi de que havia alguma mágica, porque a maioria das operações
eram Θ(1). O segredo estava no fato de que a análise para o caso
do heap de Fibonacci era uma análise amortizada. Esse tipo de análise
difere da análise do caso médio por não haver nenhuma
probabilidade envolvida, sendo considerada a média de todas as operações
executadas para uma entrada ainda assim genérica. Portanto, no caso
amortizado, o tempo exigido para executar uma sequência de operações
é calculado sobre a média de todas as operações
executadas, não tendo qualquer cálculo baseado em probabilidade
da entrada. Assim, para o heap de Fibonacci estava sendo considerado a análise
amortizada, enquanto as operações para os heaps binário
e binomial estavam sendo apresentadas com base no seu pior caso. Ficou como
uma idéia saber como seriam as colunas para o binário e o binomial
no caso de uma análise amortizada.
2. Árvores binomiais
Uma árvore binomial é uma árvore ordenada,
ou seja, a ordem em que os filhos aparecem na árvore importa, e é
definida de modo recursivo, onde uma árvore binomial Bk é constituída
de duas árvores binomiais Bk-1 que são conectadas uma à
outra pelo fato da raiz de uma ser o filho mais à esquerda da raiz
da outra.

Figura mostrando a definição recursiva
de árvore binomial (a). Os itens (b) e (c) mostram duas formas diferentes
de se visualizar uma árvore binomial (retirado do livro de aula)
3. Definição de heap binomial
Um heap binomial é constituído por uma coleção
de árvores binomiais que satisfaz às duas propriedades de heaps
binomiais:
- cada árvore tem a propriedade do heap mínimo, ou seja, a
chave de um nó na árvore deve ser maior ou igual que a chave
de seu pai.
- existe no máximo uma árvore binomial com raiz de grau k
num heap binomial, para qualquer k inteiro não negativo.
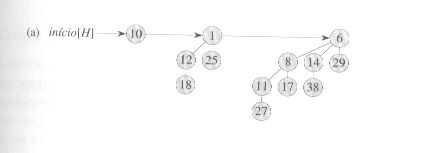
Figura mostrando um heap binomial (retirado do livro
de aula)
Uma discussão longa que se sucedeu se refere a um
aspecto relativo à segunda propriedade do heap binomial e também
sobre a representação de heaps binomiais. Embora não
apareça explicitamente nas propriedades de heaps binomiais citadas
acima, no livro é sempre usada uma representação em que
os graus das raízes das árvores binomiais aparecerem ordenadas
em ordem crescente num heap binomial. Isso deu origem a uma pergunta: se meu
heap não estiver ordenado por grau das árvores binomiais, ainda
assim continua sendo um heap binomial? Embora tenhamos chegado a um consenso
de que faltou realmente colocar essa propriedade de forma mais direta para
heaps binomiais, só consideraremos heaps binomiais os heaps em que
suas árvores binomiais estejam ordenadas pelos graus das raízes.
Caso contrário, a análise e algoritmos para as operações
executadas nesse heap certamente iriam mudar.
4. União de heaps binomiais
Dentre os procedimentos existentes, foi escolhida a união
(UNION) para assunto por ser usada como sub-rotina para a maioria das outras
operações e de ser, realmente, "a mais complicada".
A união de dois heaps binomiais H1 e H2 tem basicamente
dois passos. O primeiro intercala os heaps H1 e H2 resultando num outro heap
H. A operação de intercalação cria o heap intercalado
H que conterá as ávores binomiais dos heaps H1 e H2 e será
ordenado pelos graus das raízes em ordem monotonicamente crescente.
Portanto, esse novo heap H pode não ser um heap binomial, pelo fato
de poder existir mais de uma árvore binomial (no máximo duas)
com raízes de mesmo grau. O segundo passo portanto trata de ligar raízes
com o mesmo grau, garantindo que reste no máximo uma raiz de cada grau.
O algoritmo do livro para a operação de união está
recolocado abaixo. Em seguida analisamos com um pouco mais de detalhes as
situações que podem ocorrer na execução do segundo
passo.

Algoritmo de união para heaps binomiais (retirado
do livro de aula)
O primeiro passo simplesmente intercala os dois heaps. Para execução
do segundo passo, três ponteiros são mantidos:
- x -- aponta para a raiz da árvore atual (a qual está sendo
examinada)
- anterior-x -- aponta para raiz anterior à raiz x na lista de raízes
do heap (quando x é a primeira raiz, anterior-x vale NIL)
- proximo-x -- aponta para a raiz próxima de x na lista de raízes
(quando x é a última raiz, proximo-x vale NIL)
Assim, supondo que já temos o heap intercalado, as
seguintes situações podem ocorrer:
- caso 1: grau[x] é diferente do grau[proximo-x], ou seja, não
precisamos ligar as raízes e então só movemos os ponteiros
uma posição para frente no heap
- caso 2: aqui x é a primeira de três raízes do mesmo
grau, e o que o algoritmo faz é considerar a primeira raiz como a
única daquele grau e então passa a analisar (ligar) as outras
duas. Esse caso foi bastante ressaltado na discussão em aula do algoritmo
- caso 3 e 4: x é a primeira de duas raízes de mesmo grau
e então basta ligar essas duas, tomando cuidado para manter a estrutura
de heap mínimo na nova árvore que está sendo criada
(é isso que diferencia o caso 3 do 4, ou seja, qual raiz será
escolhida como nova raiz)
Analisando a complexidade de UNION, começamos analisando
a complexidade da intercalação. Ela leva O(lgn), onde
n é o número de nós dos heaps binomiais H1 e H2. Para
ver isso, dizemos que H1 tem n1 nós e que H2 tem n2 nós. Assim,
n = n1+n2. Pela definição de heap binomial, H1 tem no máximo
piso(lgn1)+1 raízes e H2 tem no máximo piso(lgn2)+1 raízes.
Como piso(lgn1)+piso(lgn2)+2 <= 2(piso(lgn))+2 = O(lgn), H tem
no máximo lgn raízes após a chamada do procedimento de
intercalação, o qual é portanto O(lgn). No laço
while, há no máximo piso(lgn1)+lg(n2)+2 iterações
que levam O(1) e portanto, o tempo total de UNION é O(lgn).
OBS: foram discutidas outras operações realizadas em heaps
binomiais nesse ponto da aula, como MINIMUM, EXTRACT-MIN e DECREASE-KEY. Um
ponto interessante da aula foi sobre a hipótese de qual seria a complexidade
de um eventual INCREASE-KEY para esse heap. As primeiras idéias levavam
para O(lg^2(n)) (lg ao quadrado de n), contudo, notou-se que o INCREASE-KEY
poderia ser realizado utilizando-se os procedimentos DELETE e INSERT, ambos
gastando O(lgn), o que resultaria em O(lgn) para INCREASE-KEY.
5. Definição de heaps de Fibonacci
Um heap de Fibonacci é uma coleção de árvores
que possuem a propriedade de heaps mínimos, mas essas árvores
não estão restritas a serem árvores binomiais e nem precisam
estar ordenadas por ordem de grau de suas raízes no heap. Portanto,
um heap de Fibonacci apresenta uma estrutura mais relaxada em relação
a um heap binomial, podendo conter árvores de aridades variáveis.
A estrutura para representação desse heap é mais complexa,
chegando a utilizar lista circular duplamente ligada para interligar os filhos
de um nó x. As raízes também são ligadas através
de uma lista circular duplamente ligada.

Figura mostrando um heap de Fibonacci (a) e uma estrutura
de dados representando-a (b) (retirado do livro de aula)



