
Aula dia: 09-Mai-2003
Última atualização: 14-Mai-2003
Redator: Fábio Batista Gomes - RA 022256
Em computação é muito importante a representação de problemas através de grafos. Os algoritmos básicos de grafos apresentados no livro são de grande utilidade na solução desses tipos de problemas. (Zanoni)
Um grafo G = (V, E) é caracterizado por um conjunto de vértices (V) e outro de arestas (E) que ligam os vértices entre si.
Listas de adjacências é uma das formas de representar um grafo. Consiste de um arranjo de |V| listas, uma para cada vértice. Cada lista contém os vértices adjacentes ao vértice correspondente àquela lista. Cada vértice adjacente a um vértice u é inserido na lista de adjacência de u. As figuras 22.1(b) e 22.2(b) apresentam as representações em forma de listas ligadas para grafos não-orientados e grafos orientados, respectivamente.
É uma forma preferida de representação de grafos esparsos, nos quais |E| é bem menor que |V|2. Uma propriedade importante de listas de adjacências é que, tanto para grafos orientados como não-orientados, a quantidade memória necessária para representar o grafo é Theta(V + E). Porém, não é vantajosa para verificar se há adjacência entre dois vértices quaisquer, pois teria que se percorrer a lista de adjacência completa de um determinado vértice. A maioria dos grafos apresentados no livro pressupõem essa forma de representação.

Consiste de uma matriz A = (aij) com |V| linhas e |V| colunas que representam os vértices do grafo. Se existe uma aresta entre os vértices i e j, então aij = 1; se não, aij = 0. Quando o grafo é não-orientado há uma simetria com relação à diagonal principal da matriz. Como (u, v) e (v, u) representam a mesma aresta em um grafo não-orientado, a matriz de adjacências será sua própria transposta: A = AT. Neste caso, é preferível armazenar apenas as entradas da diagonal e acima da diagonal da matriz, reduzindo quase pela metade a memória necessária. Se o grafo é orientado, cada célula da matriz representará uma aresta distinta, partindo de um vértice origem (linhas) para um vértice destino (colunas) ou vice-versa (origem na coluna e destino na linha).
Com a representação por matriz pode-se saber se dois vértices são adjacentes em tempo constante, pois basta verificar a posição correspondente na matriz. Por outro lado, independentemente do número de arestas será necessária uma quantidade de memória Theta(V2) para guardar a matriz. Portanto, matriz de adjacências é vantajosa na representação de grafos densos, nos quais |E| é próximo de |V|2, ou quando se tem grafos razoavelmente pequenos.
Nielsen: Para grafos não-ponderados (todas as arestas têm o mesmo peso) é necessário apenas 1 bit para representar a aresta. E mesmo para grafos ponderados a matriz de adjacências apresenta uma vantagem, pois pode-se atribuir o peso da aresta à célula correspondente na matriz ou (NIL, 0 ou infinito) quando não houver aresta.
Já com listas de adjacências é necessário espaço adicional para armazenar os pesos das arestas se o grafo for orientado. Por outro lado, listas de adjacências são mais robustas neste aspecto, podendo ser modificadas para admitir outras variantes de grafos.
Augusto: Existem algoritmos que utilizem a representação por matriz de incidência? Matriz de incidência é uma outra representação menos comum de grafos onde se tem uma matriz de arestas por vértices - |E| x |V|.
Zanoni: Existem alguns algoritmos que supõem a representação de matriz de incidência, porém as mais comuns são as apresentadas no livro (listas e matriz de adjacências)
Deve-se pensar também que matriz de adjacências pode utilizar apenas 1 bit para representar arestas de grafos não-ponderados, enquanto listas de adjacências gastam vários bits para cada adjacência - devem armazenar qual vértice é adjacente e ainda um ponteiro para o próximo vértice adjacente. Portanto, na prática o grafo não precisa ser totalmente denso para que a representação por matriz seja mais viável. Basta uma quantidade razoável de arestas e a representação por listas passa a ser mais espaçosa, além de mais complexa.
Busca em largura é uma das formas mais simples de percorrer todos os vértices de um grafo. O algoritmo consiste em partir de um vértice origem conhecido s e percorrer todos seus vértices adjacentes. A partir de cada vértice adjacente, que então já foram descobertos, percorrem-se os respectivos vértices adjacentes que ainda não são conhecidos até que não existam mais vértices desconhecidos.
Implementação desse algoritmo (Figura 22.3): No início todos os vértices são brancos (desconhecidos). Cada vértice torna-se acinzentado quando é descoberto pela primeira vez. Os vértices cinzas são armazenados numa fila à medida que vão sendo descobertos. Para cada vértice da fila procura-se os vértices adjacentes que ainda são brancos. Quando todos vértices adjacentes do vértice atual tiverem sido descobertos, o vértice atual torna-se preto e prossegue-se analisando o próximo vértice da fila até que esta esteja vazia. Inicia-se pelo vértice origem s tornado-o cinza e colocando-o na fila.
Durante a busca ainda são armazenadas duas informações em vetores auxiliares: a distância de cada vértice até o vértice origem (vetor d) pelo caminho percorrido, e o respectivo predecessor, ou pai, de cada vértice (vetor PI). No início, para todos vértices a distância até a origem é infinito e o predecessor é NIL. Para o vértice origem s a distância até a origem é zero e não existe predecessor (NIL). Para os demais vértices a distância é incrementada com relação à distância do predecessor (à medida que se distancia da origem) e o predecessor de cada vértice é o vértice pelo qual ele foi descoberto.
Zanoni: Um efeito colateral é que, para grafos não-ponderados, esse algoritmo já define a distância mínima a qualquer vértice partindo do vértice de origem s. Não significa que ele não possa ser usado, com alguma pequena alteração, em grafos ponderados. Porém este algoritmo já é ajustado para facilitar a obtenção do caminho mais curto.
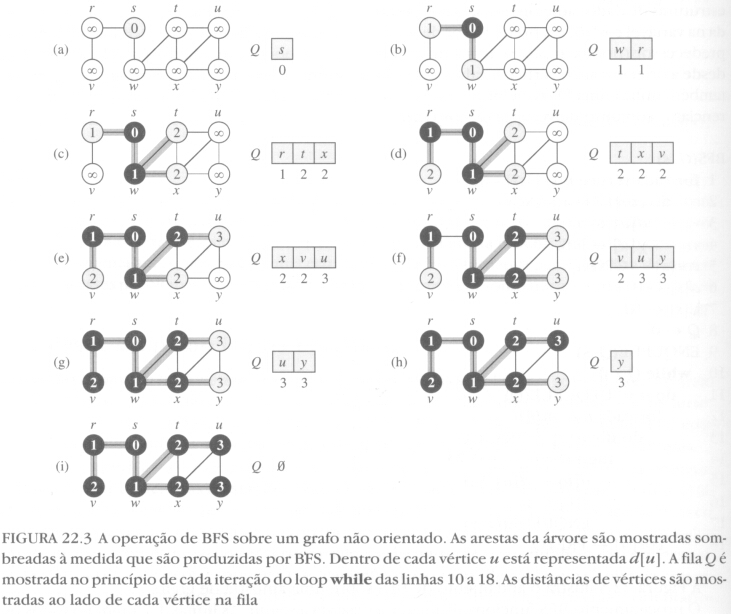
Nota: na figura 22.3 (f) falta acinzentar a aresta rs.
Análise: Assume-se a utilização de listas de adjacências para análise da complexidade desse algoritmo. É utilizada análise agregada segundo a Seção 17.1 do livro, que consiste em analisar a complexidade da soma das operações e não operação por operação.
As operações de colocar e tirar da fila têm complexidade O(1) e essas operações são realizadas no máximo uma vez para cada vértice. Portanto tem-se que a complexidade total com as operações de fila é O(V). A complexidade com a varredura total das listas de adjacências é a soma do comprimento de cada lista, que é igual a O(E). Portanto, o limite superior para o número de operações realizadas na busca em largura é O(V + E).
Em teoria de grafos falamos que o tamanho do grafo é |V| + |E|. Portando, assim como O(n) indica execução em tempo linear para algoritmos com entrada de tamanho n, a complexidade O(V + E) nos indica que a busca em largura é executada em tempo linear.
Zanoni: A ordem em que os vértices adjacentes são descobertos é aleatória, ou melhor, é definida pela implementação das listas de adjacências.
Demonstra através dos lemas e provas que no algoritmo BFS, ao final de sua execução, a variável d[v] contém o valor do menor caminho de um vértice qualquer v até o vértice origem s e o vetor PI contém todos vértices predecessores que pertencem a este caminho. Assim, para se obter o caminho mais curto do vértice s até o vértice v, basta seguir o caminho mais curto de s até PI[v] e então percorrer a aresta (PI[v], v).
Como o algoritmo é executado para grafo não-ponderado e realiza a busca em largura, qualquer outro caminho que ele tomasse para chegar a um vértice v que não fosse o caminho percorrido através dos vértices imediatamente adjacentes seria maior. E se a cada passo ele guarda informação do vértice predecessor pelo qual ele descobriu o vértice v, o caminho através destes predecessores leva ao vértice inicial s pelo menor caminho.
O procedimento BFS gera um subgrafo predecessor de G, chamado GPI. Ele é representado pelo campo PI em cada vértice.
Este subgrafo é uma árvore, pois obedece ao teorema B.2 (|EPI| = |VPI| - 1). Mostra-se ainda que todos vértices VPI são acessíveis a partir de s, pois todos os vértices em PI enxergam s, e ainda, que através destes vértices em VPI existe um caminho único simples desde s até v que também é o caminho mais curto.
PRINT_PATH(G, s, v)
1 if v = s
2 then imprimir s
3 else if PI[v] = NIL
4 then imprimir "nenhum caminho
de " s " para " v " existente."
5 else PRINT_PATH(G, s, PI[v])
6 imprimir v
O procedimento PRINT_PATH(G, s, v) imprime o caminho mais curto de s até v de forma recursiva, após BFS ter sido executado sobre o grafo G e gerado a árvore de caminho mais curto. Este algoritmo é executado em tempo linear no número de vértices do caminho impresso.