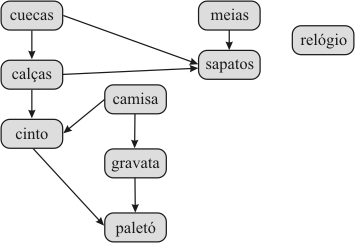
Figura 22.7: Exemplo de grafo orientado acíclico
Na qual são discutidos dois algoritmos em grafos: busca em profundidade e ordenação topológica. José Augusto Amgarten Quitzau, Patrick Henrique da Silva Brito e Camila Ribeiro Rocha são convidados a expor o assunto.
Notação.
Nesta ata de aula, a seguinte notação é utilizada:
V indica o conjunto de vértices de um grafo
E indica o conjunto de arestas de um grafo
n indica o número de vértices de um grafo, ou seja, a
cardinalidade de V. Portanto, n = |V|
m indica o número de arestas de um grafo, ou seja, a cardinalidade
de E. Portanto, m = |E|
De forma similar à busca em largura, a busca em profundidade começa a partir de um vértice. Entretanto, ao contrário da busca em largura, a busca em profundidade escolhe um descendente e já começa a examinar os seus próximos descendentes, fazendo com que a varredura no grafo seja em profundidade.
Classicamente, as semelhanças e diferenças entre as buscas em largura e profundidade são as seguintes: em ambas as buscas, parte-se de um vértice e são investigados os vértices adjacentes, sucessivamente, até que todo o grafo seja percorrido. A principal diferença é que a busca em largura utiliza uma fila para armazenar vértices que foram descobertos e precisam ser explorados, enquanto que a busca em profundidade utiliza uma pilha, fazendo com que a busca siga em profundidade. O livro texto apresenta um algoritmo recursivo para busca em profundidade sem utilizar uma pilha explícita. É importante ressaltar que todo algoritmo recursivo tem uma versão não-recursiva que utilize uma pilha explícita, mas nem todo algoritmo que utilize uma pilha possui uma versão recursiva.
Outra diferença é que existe o conceito de marcação de tempo no algoritmo de busca em profundidade (DFS) apresentado no livro. O algoritmo possui uma variável global chamada tempo que marca o passo (ou a cadência) de execução do algoritmo: a variável tempo é incrementada sempre que um vértice novo é descoberto. No algoritmo do livro, armazena-se em d[v] o instante de tempo em que o vértice v foi descoberto pela primeira vez e em f[v] o instante de tempo em que se terminou de examinar os vértices adjacentes a v. Relacionando-se as cores e os instantes de tempo associados a um vértice v, tem-se que o vértice v é BRANCO antes do tempo d[v], CINZA entre o tempo d[v] e o tempo f[v] e PRETO depois disso. Ao final do algoritmo, para todo vértice v do grafo, d[v] < f[v].
O tempo de execução de DFS é Θ(n+m). Os laços nas linhas 1-3 e 5-7 de DFS demoram Θ(n). Em uma análise mais crua, poder-se-ia dizer que DFS leva O(nm), já que DFS é Θ(n) e DFS-VISIT é O(m). Entretanto, como o procedimento DFS-VISIT é chamado uma única vez para cada vértice no grafo, pode-se utilizar análise agregada para definir um limite mais estrito do tempo de execução de DFS. O laço nas linhas 4-7 de DFS-VISIT é executado |Adj[v]| (grau do vértice v) vezes para cada vértice v do grafo. Como a somatória dos graus dos vértices de um grafo é igual a 2m (teorema da soma dos graus), o laço das linhas 4-7 em DFS-VISIT (e portanto DFS-VISIT), para todos os vértices do grafo, demora Θ(m). Conseqüentemente, o tempo total de execução de DFS é Θ(n+m).
DFS(G)
V[G] do
1 for cada vértice u pertencente a V[G] do
2 cor[u] ← BRANCO
3 π[u] ← NIL
4 tempo ← 0
5 for cada vértice u pertencente a
6 if cor[u] = BRANCO then
7 DFS-VISIT(u)
DFS-VISIT(u)
1 cor[u] ← CINZA
2 tempo ← tempo + 1
3 d[u] ← tempo
4 for cada v pertencente a Adj[u] do
5 if cor[v]
= BRANCO then
6 π[v]
← u
7 DFS-VISIT(v)
8 cor[u] ← PRETO
9 f[u] ← tempo ←
tempo + 1
Enquanto que a busca em largura forma uma árvore em largura, a busca em profundidade forma uma floresta em profundidade composta por várias árvores em profundidade. As arestas destas árvores são chamadas arestas de árvore. Além das arestas de árvore, a busca em profundidade pode classificar as arestas do grafo de entrada em outros três tipos: arestas de retorno (conectam um vértice u a um ancestral v), arestas diretas (arestas que não são de árvore e que conectam um vértice u a um descendente v) e arestas cruzadas (todas as outras arestas).
Se o grafo não for orientado, haverá uma árvore para cada componente conexo, sendo que as arestas do grafo serão classificadas em apenas dois tipos: de árvore ou retorno. Nos grafos orientados, pode-se encontrar arestas diretas e cruzadas.
Pode-se entender as arestas diretas da seguinte forma: seja o grafo orientado G = (V,E) onde V = {u,v,w} e E = {(u,v),(u,w),(v,w)}. Considere-se que a busca em profundidade, a partir do vértice u, explorou primeiro o vértice v e, em seguida, o vértice w. Portanto, as arestas (u,v) e (v,w) são arestas de árvore. Após explorar a profundidade de v, o algoritmo retorna e começa a explorar o próximo adjacente a e acessível a partir de v, que é o vértice w. Entretanto, o vértice w já foi explorado: a aresta (v,w) é classificada como uma aresta direta.
Mesmo um grafo conexo pode gerar mais de uma árvore em profundidade, desde que seja um grafo orientado. Pode-se escolher um vértice com grau de saída zero, por exemplo. Neste caso, a árvore em profundidade é composta apenas por aquele vértice. O algoritmo, portanto, escolherá um outro nó (BRANCO) e formará outra árvore.
Alexandro José Baldassin questionou se é possível saber quantas árvores são geradas. Para tanto, basta coloca um contador no laço das linhas 5-7 do algoritmo DFS, sempre que a cor for BRANCO. Todavia, a informação de quantidade de árvores pode não ser útil, já que não é uma característica do grafo, mas sim da maneira como foi feita a busca em profundidade. E, quando se usa a busca em profundiade, resultados diferentes (árvores diferentes) são igualmente bons.
A ordenação topológica é usada em grafos orientados acíclicos para ordenar linearmente seus vértices. De forma geral, se um vértice u aponta para um vértice v (possui uma aresta orientada que sai de u e chega em v), então u deve vir antes de v no resultado da ordenação. O algoritmo TOPOLOGICAL-SORT utiliza o algoritmo DFS para determinar o tempo de término sendo que, à medida que cada vértice é terminado, o vértice é colocado na cabeça de uma lista ligada. Esta lista, ao final do algoritmo, contém a ordenação topológica do grafo. O tempo de execução de TOPOLOGICAL-SORT é Θ(n+m), pois DFS demora Θ(n+m) e a inserção na lista leva O(1). Para efeito de ordenação topológica, interessa apenas o tempo de finalização do vértice v, denotado por f[v] no algoritmo DFS.
TOPOLOGICAL-SORT(G)
1 chamar DFS(G) para calcular o tempo de término f[v]
para cada vértice v
2 à medida que cada vértice é terminado, inserir
o vértice à frente de uma lista ligada
3 return a lista ligada de vértices
Túnel do tempo.
Há 20 anos atrás, no tempo em que o prof. Meidanis estudou ordenação
topológica, o algoritmo era mais sofisticado. O primeiro passo era calcular
o grau de entrada/saída de todos os vértices. Em seguida, todos
os vértices com menor grau de entrada eram inseridos em uma lista (os
primeiros a serem inseridos na lista eram os com grau de entrada igual a zero)
e então removidos do grafo. Como as arestas que saíam destes vértices
também eram removidas, outros vértices tinham seus graus diminuídos,
e o procedimento se repetia até terminarem os vértices.
Ivan Eduardo Brunetto demonstrou surpresa com a memória de elefante do
professor, que respondeu:
"O primeiro topological sort você nunca esquece!"
Como a ordenação topológica é aplicada a grafos orientados acíclicos, nunca será encontrada uma aresta de retorno, já que não há ciclos neste tipo de grafo. Na prova da correção de TOPOLOGICAL-SORT arestas de retorno são mencionadas com o intuito de demonstrar que, ao encontrar este tipo de aresta, o lema 22.11 seria inválido, quando na verdade ele é correto (prova por contradição).
Uma observação interessante sobre o TOPOLOGICAL-SORT é que pode-se iniciar por qualquer vértice. Conseqüentemente, é possível encontrar diferentes ordenações topológicas corretas para um mesmo grafo orientado acíclico. Por exemplo, considere-se o grafo orientado acíclico da figura 22.7, reproduzido abaixo.

Figura 22.7: Exemplo de grafo orientado acíclico
A tabela abaixo demonstra uma seqüência de execução do algoritmo TOPOLOGICAL-SORT que produz uma ordenação topológica distinta da apresentada no livro.
| Passo | Escolha de um vértice u e DFS(u) | Lista de saída com a ordenação topológica |
|---|---|---|
| 1 | Escolha de sapato como primeiro vértice. Ele não tem descendentes, então escreve-se sapato na cabeça da lista. |
sapato |
| 2 | Escolhe-se relógio. Não tem filhos, então escreve-se relógio na cabeça da lista. | relógio sapato |
| 3 | Escolhe-se cinto. Tem paletó como único descendente, então escreve-se paletó e em seguida cinto. | cinto paletó relógio sapato |
| 4 | Escolhe-se camisa. Tem como descendetes gravata e paletó, mas paletó já foi processado (no algoritmo DFS, paletó tem cor PRETO e portanto não é visitado). Então escreve-se gravata e em seguida camisa. | camisa gravata cinto paletó relógio sapato |
| 5 | Escolhe-se meia. Tem como único descendente paletó, que já foi processado. Então escreve-se meia. | meia camisa gravata cinto paletó relógio |
| 6 | Escolhe-se cuecas. Tem como descendentes calças, sapato (já foi processado) e cinto (já foi processado). Então escreve-se calças e depois cuecas. | cuecas |
| 7 | Não há mais vértices com cor BRANCA. O algoritmo termina e a lista contém a ordenação topológica do grafo. | cuecas calças meia camisa gravata cinto paletó relógio |
O algoritmo TOPOLOGICAL-SORT (na verdade, o algoritmo DFS) detecta a existência de ciclos, o que não deveria ocorrer em um grafo orientado acíclico. No algoritmo DFS pode-se facilmente implementar detecção de ciclo: se durante o DFS-VISIT (vide linha 5 deste algoritmo) for encontrado um nó cinza (um nó que já começou a ser explorado mas cuja exploração ainda não terminou), é sinal de que foi encontrado um ciclo.
O topological-sort não chama o DFS para cada vértice, mas sim para os vértices necessários (vértices com cor BRANCO). Às vezes ele chama começando uma nova árvore e às vezes a execução é dada dentro da recursão de DFS-VISIT. Outra observação interessante é que não é necessário ordenar a lista ligada por f[] (tempo de finalização) porque, à medida que o algoritmo termina a visita de um vértice, este vértice é inserido na cabeça da lista, garantindo que ele aparece antes de seus descendentes.
TOPOLOGICAL-SORT pode ser utilizado sempre se necessita uma ordem para execução de tarefas onde há pré-requisitos (dependências) entre tarefas. Um possível exemplo são as matérias para se cursar uma graduação: o algoritmo garante que nenhum pré-requisito será quebrado. Outro exemplo: construir um prédio. Há várias tarefas: colocar telhado, montar parede, montar porta, parede, acabamento; também há dependências: não se coloca o teto antes de subir as paredes. Ivan Eduardo Brunetto comentou que TOPOLOGICAL-SORT pode ser aplicado também a metodologias de desenvolvimento de software. André Santanchè indicou o algoritmo para ordem de compilação de arquivos (makefile).
Uma outra aplicação são programas de planilha eletrônica. Há várias células e às vezes uma célula tem uma fórmula que depende de outras células. Então, ao se alterar o conteúdo de uma célula, é necessário verificar se é necessário atualizar outras células. Para isto, pode ser feita uma ordenação topológica. Considere que uma célula tenha sido modificada. A planilha precisa saber quem depende de quem, podendo construir grafo (orientado acíclico) de todas as células que têm que ser atualizadas em virtude da modificação da célula original. Porém, não se pode ir atualizando as células em qualquer ordem! Se existe uma célula A1, uma célula B1 com fórmula que depende de A1 e uma célula C1 que depende de B1, não se pode atualizar A1, depois C1 e depois B1.
Aplicações abundam!
Para determinação de tarefas paralelizáveis, pode-se analisar a saída do DFS em busca de paralelização, algo similar à programação de atividades estudada em algoritmos gulosos. Considere-se a versão que procura maximizar o número de atividades. Depois de rodar o DFS, para cada atividade existe um intervalo definido (para a atividade representada pelo vértice u, o início é dado por d[u] e o fim é dado por f[u]). Executa-se então o algoritmo guloso que determina um conjunto de atividades máximo que podem ser executadas em seqüência. Este conjunto (caminho) de atividades é atribuído a uma pessoa e retirado do grafo. O grafo resultante continua sendo um grafo de intervalos; aplica-se o algoritmo novamente e se atribui o caminho a uma segunda pessoa, e assim sucessivamente, tantas vezes quantas forem necessárias. Este algoritmo gera o número mínimo de pessoas necessárias para execução de todas as atividades. A pergunta respondida por este procedimento é: qual o mínimo de pessoas necessárias para executar um dado conjunto de atividades? Deve-se levar em consideração que não pode haver atrasos nas tarefas. Augusto Jun Devegili fez uma comparação com redes PERT/CPM, em que atividades podem estar (ou não) em um caminho crítico. As atividades no caminho crítico, caso sejam atrasadas, acarretam atraso do prazo final para execução de todas as atividades. Atividades que não estejam no caminho crítico podem ter algum atraso sem que o prazo final seja alterado.
pg. 429, segundo parágrafo: π[u]
→ π[v]
pg. 430, linha 5 de DFS-VISIT. if cor[u]
→ if cor[v]
figuras em geral: rótulos das arestas seguem os nomes dos tipos de arestas
em inglês
pg. 431, Teorema 22.6 → Teorema 22.7
| Disciplina: | MO417 - Complexidade de Algoritmos I |
| Livro texto: | CORMEN, T. H. et alii. Algoritmos: Teoria e Prática. Tradução da 2ª edição americana: Vandenberg D. de Souza. Rio de Janeiro: Campus, 2002. |
| Redator: | Augusto Jun Devegili (RA 025620) |