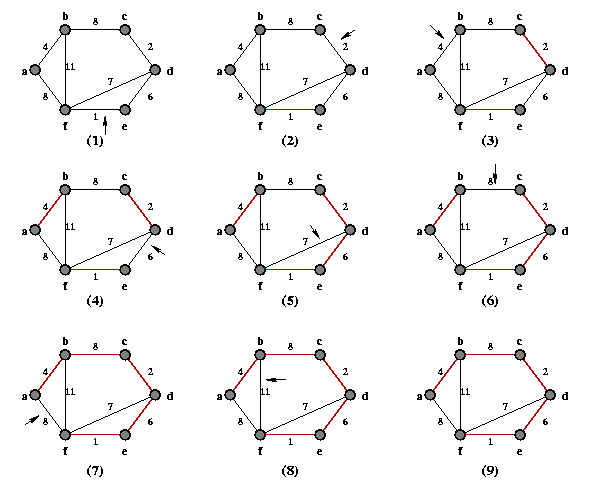
Figura 1: Exemplo de execução do algoritmo de Kruskal.
MO417 - Complexidade de Algoritmos I
Árvores Espalhadas Mínimas
Ata de Aula: 16/05/2003
Redator: José Augusto Amgarten Quitzau
Introdução.
Considere o seguinte problema:
Uma companhia telefônica deseja criar uma rede interligando um conjunto de cidades. O custo para unir duas cidades por meio de cabos é conhecido mas, como toda boa companhia, esta deseja minimizar seus gastos, fazendo as ligações mais baratas possíveis sem deixar de cobrir nenhuma das cidades.
Este problema, assim como muitos outros semelhante, se resume a achar uma Árvore Espalhada Mínima para um grafo conhecido, problema que pode ser enunciado da seguinte forma:
Dado um grafo G=(V,E) com uma função "peso" que associa valores reais w às arestas de E, deseja-se encontrar uma árvore T=(V,E') onde E' está contido em E e a soma dos pesos das arestas em E' é mínima.
Há uma solução genérica para este problema, apresentada abaixo, que serve de base para dois algoritmos bastante conhecidos para árvores espalhadas mínimas: os algoritmos de Kruskal e Prim. O algoritmo genérico mantém um conjunto de arestas A e a seguinte invariante:
A cada iteração, A é subconjunto do conjunto de arestas de uma árvore espalhada mínima.
O algoritmo mantém esta invariante adicionando ao conjunto A, a cada iteração, uma aresta (u,v) de maneira que a união de A com (u,v) seja um subconjunto de uma árvore espalhada mínima. Pelo fato de esta aresta manter a propriedade de A de ser um subconjunto de arestas de uma árvore espalhada mínima, ela é chamada de aresta segura.
O algoritmo genérico para Árvores Espalhadas Mínimas é apresentado logo abaixo:
GENERIC-MST(G,w)
1 A := {}
2 while A não forma uma árvore espalhada
3 do encontre uma aresta (u,v) que é segura para A
4 A := A união {(u,v)}
5 return A
Dois outros conceitos relacionados a árvores espalhadas mínimas são os conceitos de corte em um grafo e de arestas leves.
Um corte em um grafo não direcionado G=(V, E) é uma partição de V em dois conjuntos (S e V\S). Uma aresta (u,v) pertencente a E cruza o corte (S, V\S) se um dos vértices adjacentes a ela está em S e o outro em V\S. Dizemos que um corte respeita um conjunto A de arestas se nenhuma aresta pertencente a A cruza o corte.
Uma aresta cruzando um corte é considerada uma aresta leve se seu peso for o menor dentre os pesos das arestas que cruzam o mesmo corte. Note que, embora o peso seja mínimo, várias arestas podem ter pesos iguais, o que significa que várias arestas podem ser uma aresta leve em um determinado corte.
Teorema 23.1: Seja G=(V,E) um grafo conexo e não orientado com uma função "peso" que associa valores reais w às arestas em E. Seja A um subconjunto de E que está incluído em alguma árvore espalhada mínima de G. Seja (S, V\S) qualquer corte de G que respeita A e seja (u,v) uma aresta leve cruzando (S, V\S). Então, a aresta (u,v) é uma aresta segura para A.
O Teorema 23.1 nos dá uma idéia melhor de como é possível encontrar uma aresta segura na linha 3 do algoritmo GENERIC-MST. De fato, tanto o algoritmo de Kruskal quanto o de Prim mantém um conjunto A de arestas e, direta ou indiretamente, procuram por arestas leves de um corte que respeite A. Por outro lado, esses algoritmos se baseiam mais no corolário enunciado a seguir:
Corolário 23.2: Seja G=(V,E) um grafo conexo e não direcionado com uma função "peso" que associa valores reais w às arestas em E. Seja A um subconjunto de E contido em alguma árvore espalhada mínima de G e seja C=(VC,, EC) uma componente conexa (árvore) na floresta GA=(V,A). Se (u,v) é uma aresta leve conectando C a alguma outra componente em GA, então (u,v) é uma aresta segura para A.
Os Algoritmos de Kruskal e Prim.
Ambos os algoritmos de Kruskal e Prim seguem o esquema básico do algoritmo genérico apresentado na seção anterior. A diferença entre os dois está na forma como cada um escolhe uma aresta segura na linha 3. No algoritmo de Kruskal, o conjunto A é uma floresta cujas componentes conexas vão se unindo a cada iteração. Já no algoritmo de Prim, A nunca deixa de ser uma árvore, uma vez que a aresta segura incluída a cada passo une um vértice que está fora da árvore a um vértice que já pertence a ela.
O Algoritmo de Kruskal
O algoritmo de Kruskal começa com uma floresta de árvores formadas por apenas um vértice e procura, a cada passo, uma aresta que, além de conectar duas árvores distintas da floresta, possua peso mínimo. Suponha que, numa determinada iteração, o algoritmo escolheu a aresta (u,v) para ser inserida no conjunto A e que a aresta (u,v) conecte a árvore C1 à árvore C2. Note que, dentre todas as arestas que conectam duas componentes distintas nesta iteração, (u,v) é uma das que possui o menor peso, pois ela foi escolhida assim. Logo, nesta iteração, para qualquer corte que separe u de v, (u,v) é uma aresta leve (simplesmente pelo fato de não haver outra aresta com peso menor separando duas componentes nesta iteração). Assim, (u,v) certamente é uma aresta leve que conecta C1 a uma outra componente conexa (no caso, C2) da floresta determinada por A, o que significa que (u,v), pelo corolário 23.2, é uma aresta segura para A.
A implementação do algoritmo de Kruskal, tal como mostrada no livro Introduction to Algorithms utiliza a estrutura de dados de conjuntos disjuntos para testar se dois vértices pertencem a uma mesma componente conexa ou não. A princípio, o conjunto de arestas é ordenado em ordem crescente de peso. As arestas são pegas uma a uma, em ordem, e o algoritmo executa uma chamada da função FIND-SET(u) para cada vértice adjacente a elas. Se os vértices não pertencerem ao mesmo conjunto, o que significa que a aresta une vértices de componentes distintas, a aresta é inserida em A e os conjuntos de u e v são unidos com uma chamada do procedimento UNION. Veja uma versão do algoritmo de Kruskal em pseudocódigo logo abaixo:
MST-KRUSKAL(G,w)
1 A := {}
2 for cada vértice v em V[G]
3 do MAKE-SET(v)
4 Ordene as arestas de E em ordem crescente de peso (w)
5 for cada aresta (u,v), tomadas em ordem crescente de peso (w)
6 do if FIND-SET(u) != FIND-SET(v)
7 then A := A união {(u,v)}
8 UNION(u,v)
9 return A
A Figura 1 exemplifica uma execução do algoritmo de Kruskal. Note que as arestas são "visitadas" em ordem crescente de peso (no caso, 1, 2, 4, 6, 7, 8, 8 e 11) e, para que uma aresta seja inserida no conjunto A (aqui representado pelas arestas vermelhas), os seus vértices adjacentes devem pertencer a componentes diferentes. Note que nos passos 5, 7 e 8, as arestas verificadas acabam não sendo inseridas no conjunto A. Na figura, em cada passo, a aresta indicada é analisada (linha 6 do algoritmo) e o fato de uma aresta ser inserida ou não só é percebido no passo seguinte. Podemos entender os passos 1 a 8 na figura como "fotos" do grafo exatamente no momento em que o teste da linha 6 é executado. A "foto" 9 foi tirada depois do término do algoritmo.
|
Figura 1: Exemplo de execução do algoritmo de Kruskal. |
O tempo de execução do algoritmo de Kruskal depende muito do tipo de implementação da estrutura de dados para conjuntos disjuntos. Aqui, assumimos a implementação de florestas com ambas as heurísticas de união por posto e compressão de caminhos, uma vez que esta é a implementação mais eficiente conhecida. Assim, linhas 1 e 9 são executadas em tempo O(1). A ordenação das arestas na linha 4 pode ser executada em O(E lgE). Em conjunto, pela implementação usando florestas, as |V| operações de MAKE-SET feitas na linha 3 e as O(E) operações de FIND-SET e UNION no loop das linhas 5-8 são feitos em tempo O((V+E)alfa(V)), onde alfa é uma função de crescimento extremamente lento. Uma vez que assumimos que G é um grafo conexo, |E|>=|V|-1, logo, as operações sobre conjuntos disjuntos levam tempo O(E alfa(V)). Sabendo que alfa(V) = O(lgV) = O(lgE), o tempo de execução total para o algoritmo de Kruskal é O(E lgE). Note ainda que |E| < |V|2, o que significa que lg|E| = O(lgV2) = O(2lgV) = O(lgV), portanto, podemos determinar o tempo de execução do algoritmo de Kruskal como sendo O(E lgV).
O Algoritmo de Prim
Assim como o algoritmo de Kruskal, o algoritmo de Prim também é um caso especial do algoritmo genérico. Neste caso, porém, ao invés de conectar árvores de uma floresta, o algoritmo mantém uma única árvore que cresce a cada iteração com a inserção de um vértice. Veja uma versão do algoritmo abaixo, em pseudocódigo:
MST-PRIM(G,w,r)
1 for cada u em V[G]
2 do chave[u] := infinito
3 pai[u] := NIL
4 chave[r] := 0
5 Q := V[G]
6 while Q != {}
7 do u := EXTRACT-MIN(Q)
8 for cada v em Adj[u]
9 do if v pertence a Q e w(u,v) < chave[v]
10 then pai[v] := u
11 chave[v] := w(u,v)
Os parâmetros do procedimento MST-PRIM são um grafo conexo G, um vetor w de pesos associados às arestas de G e um vértice r, que será a raiz da árvore espalhada. Ao final da linha 5, o algoritmo se encontra na seguinte situação: todos os vértices de G estão em uma fila de prioridade mínima Q, e todos os vértices, com exceção de r, têm chave igual a infinito, enquanto r tem chave igual a 0.
No loop das linhas 6-11, os vértices de G são extraídos da fila de prioridades um de cada vez. Não é difícil de ver que o primeiro vértice a sair é a raiz (r), uma vez que ele é o único elemento com uma chave menor que infinito até a linha 5. Toda vez que um vértice v sai da fila, todos os seus vizinhos são visitados e, se a chave de um vizinho for maior que o peso da aresta que liga v a este vizinho, tanto a chave quanto o pai do vizinho são alterados: a chave passa a ser o peso da aresta que liga este vizinho a v e o pai passa a ser o próprio vértice v.
Enquanto um vértice v está na fila, pai[v] aponta para o vértice vizinho de v que já está na árvore espalhada mínima e que é ligado a v pela aresta de menor peso entre todas as arestas que conectam v a um vértice atualmente na árvore. O peso da aresta (v, pai[v]) é o valor de chave[v] e, em qualquer iteração do comando while na linha 6, qualquer vértice v que está na fila Q com valor de chave[v] menor que infinito é vizinho de algum vértice da árvore espalhada mínima pela aresta pai[v]. Quando um vértice v sai da fila, tanto ele quanto a aresta que o liga a seu pai passam a pertencer à árvore espalhada mínima e seu pai nunca mais será alterado.
Ao final do algoritmo, o conjunto A retornado pelo algoritmo genérico corresponde ao conjunto formado pelas arestas (v, pai[v]) de todos os vértices em G diferentes de r. O peso total da árvore é a soma dos valores chave[v].
A Figura 2 mostra um exemplo de execução do algoritmo de Prim. Os números em vermelho representam os valores das chaves, enquanto pequenas setas vermelhas indicam os pais dos vértices. Vértices que estão fora da fila ou que possuem pais "NIL" não têm setas vermelhas. Cada passo na figura pode ser considerado como sendo uma "foto" do grafo exatamente no momento do teste do comando while na linha 6. Assim, o passo 1 representa o grafo tal como ele se encontra logo após a execução da linha 5, com todos os vértices com chave igual a infinito, com exceção de f, que é a raiz, e todos os pais iguais a "NIL". O passo 2 mostra o resultado da primeira iteração do comando while. Nele, os vizinhos da raiz já tem um valor de chave diferente de infinito e o campo "pai" apontando para a raiz. Note que enquanto um vértice não sai da fila de prioridade, seu pai não é fixo: o pai do vértice d muda entre os passos 2 e 3. Quando um nó é extraído da fila, passa a fazer parte de um conjunto S e seu pai passa a ser definitivo.
|
Figura 2: Exemplo de execução do algoritmo de Prim. |
O desempenho do algoritmo de Prim depende da forma como a fila de prioridades Q é implementada. Se for implementada usando um heap de Fibonacci, as três primeiras linhas do algoritmo serão executadas em tempo O(V), a linha 4 em O(1), a linha 5 em O(V), uma vez que corresponde a |V| operações de INSERT. O comando while da linha 6 é iterado Theta(V) vezes. Portanto, o conjunto de todas as vezes em que a linha 7 é executada toma tempo O(V lgV), pois cada operação EXTRACT-MIN leva tempo O(lgV). Como para cada vértice, todas as arestas adjacentes podem ser visitadas pelo loop das linhas 8-11, podemos dizer que as linhas 10 e 11 são executadas O(E) vezes. A linha 10 leva tempo O(1) para ser executada, enquanto a linha 11 leva tempo amortizado O(1) se a implementação da fila utilizar um heap de Fibonacci. Ao todo, as linhas que mais contribuem para o tempo de execução do algoritmo são as linhas 7, 10 e 11. A soma de suas "contribuições" é O(E+VlgV).
Como o Teorema 23.1 se enquadra nos Algoritmos de Kruskal e Prim?
No algoritmo de Prim, é fácil identificar o corte e ver que a aresta escolhida é uma aresta leve, pois a cada iteração, os vértices que não estão na fila de prioridade são os vértices que formam o conjunto S do corte. O corte (S,V\S) respeita A, uma vez que se v ∈ S entá pai[v] ∈ S. Os vértices na fila de prioridade formam o conjunto V\S e, em especial, os vértices que têm o valor da chave diferente de infinito são os vértices adjacentes às arestas que cruzam o corte (S, V\S). Extrair o mínimo da pilha é visivelmente pegar uma das arestas que cruzam o corte e que possui menor peso, ou seja uma aresta leve do corte que, pelo Teorema 23.1, é uma aresta segura.
A Figura 3 ilustra um grafo no meio da execução do algoritmo de Prim. Nela, vértices cinza fazem parte do conjunto S e vértices brancos, do conjunto V\S. As arestas em vermelho são arestas que cruzam o corte. Note que o conjunto A de arestas já forma uma árvore com os vértices de V e que o corte respeita A. Pelo Teorema 23.1, dentre as arestas vermelhas, qualquer uma de peso mínimo é segura para A, pois é uma aresta leve para este corte e, como dito anteriormente, este corte respeita A.
|
Figura 3: Um corte no grafo durante a execução do algoritmo de Prim. |
No algoritmo de Kruskal, enxergar o corte é um pouco mais difícil porque o corte geralmente não é único. Quando uma aresta (u,v) é inserida em A pelo algoritmo de Kruskal, ela é a aresta de menor peso dentre todas as arestas que unem duas componentes conexas do grafo GA=(V,A). Isso significa que qualquer corte que respeite A e que separe u de v tem em (u,v) uma aresta leve. Para tornar a visualização mais fácil, vamos identificar um dos possíveis cortes. Tome S como sendo o conjunto de vértices pertencentes à componente conexa da qual u faz parte no grafo GA=(V,A). Note que este corte respeita A, pois a componente conexa de u é determinada por arestas de A, assim, (u,v) certamente é uma aresta que cruza o corte (S, V\S) e, como (u,v) foi escolhida de tal maneira que o peso de (u,v) fosse o menor dentre todas as arestas que uniam componentes conexas diferentes em GA, então (u,v) só pode ser uma aresta leve deste corte. Assim, pelo Teorema 23.1, (u,v) é uma aresta segura. Note que, tomando S como sendo o conjunto de vértices pertencentes à componente conexa da qual v faz parte, também chegaríamos à conclusão de que (u,v) é uma aresta segura.
A Figura 4 mostra vários cortes possíveis para o grafo durante a execução do algoritmo de Kruskal. Neste caso, o peso da aresta vermelha é o menor dentre todos os pesos de arestas que ligam vértices de componentes distintas. Assim, a aresta vermelha é uma aresta leve para qualquer corte que respeite A (aqui representado pelas arestas mais grossas). As linhas tracejadas representam diferentes cortes no grafo que respeitam o conjunto A e são cruzados pela aresta vermelha. Como os cortes respeitam A e passam por uma aresta que possui o menor peso dentre todas as arestas que possam fazer parte de um corte "respeitador" de A no grafo, tal como ele está, a aresta vermelha certamente é uma aresta leve para qualquer um destes cortes. Assim, pelo Teorema 23.1, a aresta vermelha é uma aresta segura para A.
|
Figura 4: Possíveis cortes no grafo durante a execução do algoritmo de Kruskal. |
Para quem gosta de Provas
Prova do Teorema 23.1.
Seja T uma árvore espalhada mínima que contenha A. Vamos assumir que T não contém a aresta leve (u,v), pois se contém, é claro que (u,v) é uma aresta segura para A. A idéia da prova é construir uma nova árvore T ′ que contenha a união de A com {(u,v)} e para isso será usada a técnica de cortar e colar, tal como foi usada em muitas provas, principalmente nas aulas sobre programação dinâmica.
Note que, se T é uma árvore espalhada do grafo G que não contém (u,v), então a aresta (u,v) determina um ciclo no caminho p de u a v na árvore T. Um corte que respeite A e separe u de v certamente é cruzado por outra aresta neste caminho, uma vez que u está em um lado do corte e v está do outro lado. Assim, sejam (S,V\S) um corte que respeite A e separe os vértices u e v e (x,y) uma aresta pertencente ao caminho p que cruze o corte (S,V\S). Note que (x,y) não está em A, pois o corte (S,V\S) respeita A. A remoção de (x,y) da árvore T quebra esta árvore em duas componentes conexas, que podem ser unidas por (u,v) formando uma nova árvore T ′ (lembre-se que a aresta (x,y) fazia parte do ciclo formado pelo caminho p mais a aresta (u,v)).
Agora, resta mostrar que T ′ é uma árvore espalhada mínima. É importante lembrar que, pelo enunciado do Teorema, a aresta (u,v) é uma aresta leve do corte (S,V\S), o que significa que, se (x,y) também cruza o mesmo corte, então o peso de (x,y) não pode ser menor do que o peso de (u,v), caso contrário, (u,v) não seria uma aresta de corte. Assim:
w(T ′) = w(T) – w(x,y) + w(u,v) <= w(T).
Mas w(T)<=w(T ′), pois T é uma árvore espalhada mínima. Assim, w(T)=w(T ′), o que significa que T ′ é uma árvore espalhada mínima.
Note que A está contido em T e (x,y) não pertence a A, logo, A está contido em T ′ e a união de A com (u,v) é um subconjunto de T ′, o que significa que (u,v) é uma aresta segura para A.
Prova do Corolário 23.2.
Basta notar que o corte (VC, V\VC) respeita A e (u,v) é uma aresta leve para este corte. Assim, pelo Teorema 23.1, (u,v) é segura para A.
Bonus Track: Um pseudocódigo para MST-PRIM usando heap de Fibonacci explicitamente e retornando A.
MST-PRIM(G,w,r)
1 A := {}
2 MAKE-FIB-HEAP(Q)
3 for cada u em V[G]
4 do key[u] := infinito
5 pai[u] := NIL
6 FIB-HEAP-INSERT(Q,u)
7 FIB-HEAP-DECREASE-KEY(Q,r,0)
8 while Q não estiver vazia
9 do u := FIB-HEAP-EXTRACT-MIN(Q)
10 A := A união {(u, pai[u])}
11 for cada v em Adj[u]
12 do if v pertence a Q e w(u,v) < key[v]
13 then pai[v] := u
14 FIB-HEAP-DECREASE-KEY(v, w(u,v))
15 return A