a)

b)

c)

d)

e)
f)
g)
Ata de Aula (23/05)
Disciplina de Complexidade de Algoritmos
Professor: Dr. João Meidanis
Assunto: Caminhos mais curtos de única origem (Parte II)
Livro-texto: Algoritmos – Thomas H. Cormen, et. al
Autor: Eduardo Akira Yonekura
RA: 025989
Esta ata cobre os seguintes tópicos:
Caminhos mais curtos de única origem em grafos acíclicos orientados.
Algoritmo de Dijkstra.
Início da aula
Nota do Autor: O Prof. João Meidanis, logo no início da aula, explicou-nos a pronúncia correta de Dijkstra (nos EUA, ele é chamado de "Daistra", enquanto que na Holanda é "Deistra"). Como ele era holandês, convencionou-se portanto que ele seria chamado, a partir deste momento, de "Deistra".
Prof. João Meidanis: Como melhorar assintoticamente o tempo de execução do algoritmo de Bellman-Ford (cujo tempo é O(VE))?
Guilherme: Utilizando uma ordenação topológica dos vértices de um gao (grafo acíclico orientado), fazendo então apenas uma passagem sobre os vértices (na sequência topologicamente ordenada), temos então, um tempo Theta(V + E).
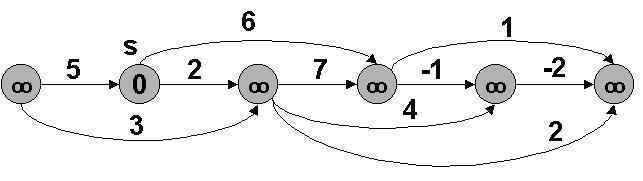
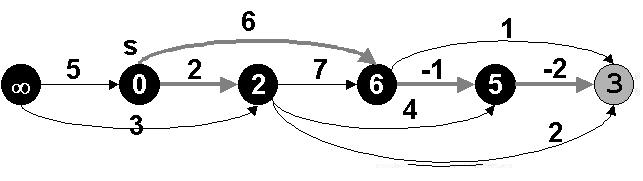
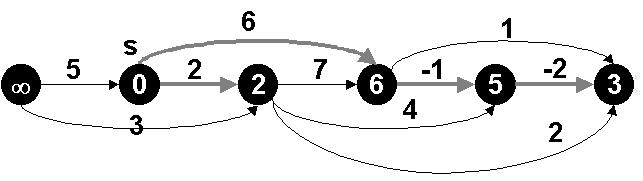
Nota do Autor: Para acompanhar melhor a explicação do algoritmo de caminhos mais curtos de única origem em grafos acíclicos orientados, considere o algoritmo e a figura abaixo (retirados do livro-texto).
DAG-SHORTEST-PATHS(G,w,s)
1 ordenar topologicamente os vértices de G
2 INITIALIZE-SINGLE-SOURCE(G,s)
3 for cada vértice u tomado em sequência topologicamente ordenada
4 do for cada vértice v pert Adj[u]
5 do RELAX(u,v,w)
|
a) |
b) |
|
c) |
d) |
|
e) |
f) |
|
g) |
|
Figura 1. A execução do algoritmo para caminhos mais curtos em um grafo acíclico orientado. Os vértices são ordenados topologicamente da esquerda para a direita. O vértice de origem é s. Os valores de d são mostrados dentro dos vértices, e arestas sombreadas indicam os valores de pi. (a) A situação antes da primeira iteração do loop for das linhas 3 a 5. (b) – (g) A situação após cada iteração do loop for das linhas 3 a 5. O vértice enegrecido recentemente em cada iteração foi usado como u nessa iteração. Os valores mostrados na parte (g) são os valores finais.
Alexandro: O algoritmo de Bellman-Ford funciona para gao?
Prof. João Meidanis: Sim.
Prof. João Meidanis: Onde começa o vértice s?
Thiago: O vértice s pode ser qualquer um dos vértices, porém à esquerda do vértice s todos os outros vértices tem o valor ∞ , só que nunca são atualizados.
Prof. João Meidanis: Todos os vértices neste caso ficam com o valor ∞ e nunca são relaxados (O Professor dirige-se então ao quadro para exemplificar).
![]()
Figura 2.
Camila: Não entendi direito o exemplo com diagramas PERT (program evaluation and review technique)...
Prof. João Meidanis: No exemplo de diagramas PERT, não estamos interessados no caminho mais curto, e sim no mais longo, para sabermos quanto vai durar um projeto.
Ivan: Tem que ser obrigatoriamente acíclico?
Prof. João Meidanis: Sim.
Diagramas PERT
Os Diagramas PERT (Program Evaluation and Review Technique) desenvolvem uma descrição de um conjunto de tarefas de um projeto, ou seja, uma representação em um grafo das tarefas que devem ser executadas desde o começo até o final de um projeto (onde as arestas representam tarefas a serem executadas, e os pesos de arestas representam os tempos necessários para a execução de determinadas tarefas). Se a aresta (u,v) entra no vértice v e a aresta (v,x) sai de v, então o serviço (u,v) deve ser executado antes do serviço (v,x). Uma aplicação interessante do algoritmo DAG-SHORTEST-PATHS surge na determinação de caminhos críticos (caminhos mais longos) em diagramas PERT, o que corresponde ao tempo mais longo para execução de uma sequência ordenada de tarefas. Este caminho crítico pode ser encontrado de duas maneiras:
Problema NP – difícil para grafos em geral (incluindo cíclicos), não para grafos acíclicos.
Ivan: Neste caso então, concluímos que um ciclo representaria um deadlock.
Alexandro: Theta(V+E) é bom?
Prof. João Meidanis: Sim, é o melhor que tem. Porém, Theta(V+E) só tem sentido se o grafo for não-conexo.
Thiago: Por quê?
Prof. João Meidanis: Em um grafo conexo V+E "torna-se" E.
Prof. João Meidanis: Como funciona o algoritmo de Dijkstra?
Nota do Autor: Para acompanhar melhor a explicação do algoritmo de Dijkstra, o autor "simulou" o exemplo do livro-texto no software ASTRAL, desenvolvido no próprio IC-UNICAMP.
Algoritmo de Dijkstra – Exemplo do livro-texto
DIJKSTRA(G,w,s)
1 INITIALIZE-SINGLE-SOURCE(G,s)
2 S <- ∅
3 Q <- V[G]
4 while Q ≠ ∅
5 do u <- EXTRACT-MIN(Q)
6 S <- S U {u}
7 for cada vértice v pert Adj[u]
8 do RELAX(u,v,w)
|
a) |
b) |
|
c) |
d) |
|
e) |
f) |
Figura 4. A execução do algoritmo de Dijkstra. A origem é o vértice mais à esquerda. As estimativas de caminhos mais curtos são mostradas sobre os vértices, e as arestas em vermelho indicam valores de predecessores. Vértices vermelhos estão no conjunto S, e vértices azuis estão na fila de prioridade mínima Q = V – S. (a) A situação imediatamente antes da primeira iteração do loop while das linhas 4 a 8. O vértice vermelho tem o valor de d mínimo e é escolhido como vértice u na linha 5. (b) – (f) A situação após cada iteração sucessiva do loop while. O vértice branco em cada parte é escolhido como vértice u na linha 5 da próxima iteração. Os valores de d e pi mostrados na parte (f) são os valores finais.
André: O algoritmo de Dijkstra não permite arestas com pesos negativos. Portanto, é menos genérico que o algoritmo de Bellman-Ford. Contudo, é mais rápido que Bellman-Ford. Pode ser feita uma comparação com o algoritmos de busca em largura (BFS), pois marca de preto os vértices que já foram visitados e também com o algoritmo de Prim (árvore geradora mínima), por causa da fila de prioridade mínima.
Prof. João Meidanis: Quantas vezes o algoritmo de Dijkstra relaxa cada aresta?
André: Apenas uma vez.
Prof. João Meidanis: O que significa a chave na fila de prioridade mínima?
André: É um limite superior na distância de s a u.
Alexandro: Suponha um grafo com arestas de peso negativo. Seria possível, no algoritmo de Dijkstra, adicionarmos uma constante para cada aresta, de modo que os pesos negativos fiquem positivos?
Prof. João Meidanis: Não. Muda a natureza do problema (O Professor dirige-se então ao quadro para exemplificar).

Figura 5.
Repare que: -1 + 10 + 4,5 = 13,5, ao passo que, 5 + 4+ 3+ 1 = 13. Ou seja, escolheríamos o caminho 5 + 4+ 3+ 1 = 13, por ser mais curto.
Suponha que adicionemos a constante 1 para cada peso.
 Figura 6.
Figura 6.
Agora, tem-se que:
0 + 11+ 5,5 = 16,5, ao passo que, 6 + 5 + 4+ 2 = 17. Repare que agora, escolheríamos o caminho 0 + 11+ 5,5 = 16,5.
Thiago: O conjunto S não serve pra nada...
Prof. João Meidanis: É verdade, pois ele sempre começa com ∅ e termina com todos os vértices. Porém, sugiro que, em termos de implementação, a inclusão do conjunto S seja importante, especialmente para fins de depuração.
Nota do Autor: Neste momento, a colega Camila fez uma observação sobre o falecimento de Dijkstra, fato este que ocorreu infelizmente no ano passado.
Prof. João Meidanis: Vamos falar agora a respeito das implementações do algoritmo de Dijkstra. Como funciona esta implementação em O(V^2)?
Marcelo: Primeiramente, devemos armazenar os vértices em um arranjo (vetor). As operações INSERT e DECREASE-KEY levam O(1). EXTRACT-MIN consome O(V) pois é necessário pesquisar pelo arranjo inteiro, o que dá portanto um tempo total de O(V^2 + E) = O(V^2).
Prof. João Meidanis: Como é possível melhorar este tempo de O(V^2)?
Bruno: Utilizando um heap binário (se o grafo for suficientemente esparso, ou seja, se E = o(V^2/lg V) ), podemos conseguir um tempo de O(E lg V), se todos os vértices forem acessíveis a partir da origem. Com Fibonacci, podemos melhorar ainda mais alcançando o tempo de O(V lgV + E).
Prof. João Meidanis: O(V lgV + E) é melhor ou pior que os outros?
Thiago: Depende...
Nota do Autor: Para esclarecer melhor esta questão, de acordo com as palavras contidas no livro-texto (pg 474, parág. 1º ): "Historicamente, o desenvolvimento de heaps de Fibonacci foi motivado pela observação de que, no algoritmo de Dijkstra, existem tipicamente muito mais chamadas DECREASE-KEY que chamadas EXTRACT-MIN; assim, qualquer método de redução do tempo amortizado de EXTRACT-MIN produziria uma implementação assintoticamente mais rápida do que aquela que utiliza heaps binários"
Prof. João Meidanis: Vocês repararam que não são utilizados heaps binomiais, somente heaps binários e de Fibonacci?
Nota do Autor: Neste momento, começou-se uma "discussão" a respeito de qual implementação da fila de prioridade é a melhor. Chegou-se então à seguinte conclusão, de acordo com as palavras do Prof. João Meidanis:
Prof. João Meidanis: Em condições normais, Fibonacci é sempre melhor, se todos os vértices forem acessíveis a partir de s.
Término da aula.