Disciplina de Complexidade de Algoritmos

Professor: Dr. João Meidanis

Assunto: Caminhos mais curtos de todos os pares (Capítulo 25)

Livro-texto: Algoritmos – Thomas H. Cormen, et. al

Autor: Eduardo Akira Yonekura

RA: 025989

Esta ata cobre os seguintes tópicos:

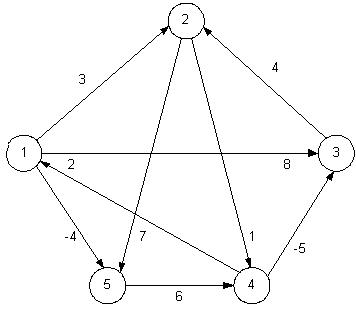
Considere o problema de encontrar caminhos mais curtos entre todos os pares de vértices em um grafo. Esse problema poderia surgir, por exemplo, na elaboração de uma tabela de distâncias entre todos os pares de cidades para um atlas rodoviário.

Tem-se um grafo orientado ponderado G = (V,E) com uma função peso w: E->R que mapeia arestas como pesos de valores reais. Deseja-se encontrar, para todo par de vértices u, v ∈ V, um caminho mais curto (de peso mínimo) desde u até v, onde o peso de um caminho é a soma dos pesos de suas arestas constituintes. É desejável que a saída esteja em uma forma tabular: a entrada na linha u e na coluna v deve ser o peso de um caminho mais curto desde u até v. É importante salientar que todos os algoritmos descritos nesta ata fazem uso de uma representação do grafo como uma matriz de adjacências.

Nesta seção, é apresentado um algoritmo de programação dinâmica para o problema de caminhos mais curtos de todos os pares sobre um grafo orientado G = (V,E). Recapitulando então os passos necessários para desenvolver um algoritmo de programação dinâmica:

1. Caracterizar a estrutura de uma solução ótima.
2. Definir recursivamente o valor de uma solução ótima.
3. Calcular o valor de uma solução ótima de baixo para cima.

1. A estrutura de um caminho mais curto

Primeiramente, considere um caminho mais curto p desde o vértice i até o vértice j, e suponha que p contenha no máximo m arestas (suponha também que não exista nenhum ciclo de peso negativo). Se os vértices i e j são distintos (caso contrário p tem peso 0 e nenhuma aresta), então decompomos o caminho p em i ~^p’ k -> j, onde o caminho p’ contém no máximo m-1 arestas. Pelo lema 24.1, p’ é um caminho mais curto desde i até k; desse modo, d (i,j) = d (i,k) + w_kj

2. Fórmula recursiva para o problema de caminhos mais curtos de todos os pares

Considere l_ij^(m) o peso mínimo de qualquer caminho desde o vértice i até o vértice j que contém no máximo m arestas. Portanto, tem-se que, para m = 0 (ou seja, existe um caminho mais curto desde i até j sem arestas se, e somente se i = j):

lij(0) =	0, se i = j
	∞ , se i ≠ j

Para m>= 1, tem-se que:

l_ij^(m) = min (l_ij^(m-1), min_1<=k<=n { l_ik^(m-1) + w_kj }) = min_1<=k<=n { l_ik^(m-1) + w_kj })

onde:

l_ij^(m-1) – peso do caminho mais curto desde i até j, que consiste no máximo em m-1 arestas

min_1<=k<=n{ l_ik^(m-1) + w_kj } - peso mínimo de qualquer caminho desde i até j, que consiste no máximo em m arestas, obtido pelo exame de todos os possíveis predecessores k de j.

3. Cálculo dos pesos de caminhos mais curtos de baixo para cima

Dadas as matrizes L^{(m - 1)} e W, o algoritmo abaixo retorna a matriz L^(m), ou seja, ele estende os caminhos mais curtos calculados até agora por mais uma aresta.

EXTEND-SHORTEST-PATHS(L,W)

1 n <- linhas[L]

2 seja L’ = (l_ij) uma matriz n x n

3 for i <- 1 to n

4 do for j<- 1 to n

5 do l’_ij <- ∞

6 for k <- 1 to n

7 do l’_ij <- min (l’_{ij ,} l_ik + w_kj)

8 return L’

É possível perceber, através das substituições abaixo, a relação do algoritmo EXTEND-SHORTEST-PATHS com a multiplicação de matrizes (algoritmo MATRIX-MULTIPLY)

l^(m-1) por a,

w por b,

l^(m) por c,

min por +,

+ por *,

Idealmente, deve ser observada as propriedades comutativa, elemento neutro, associativa e distributiva de uma operação com relação à outra.

MATRIX-MULTIPLY(A,B)

1 n <- linhas[A]

2 seja C uma matriz n x n

3 for i <- 1 to n

4   do for j<- 1 to n

5      do c_ij <- 0

6     for k <- 1 to n

7       do c_ij <- c_ij + a_{ik *} b_kj

8 return C

Como descrito no algoritmo abaixo, calcula-se então os pesos de caminhos mais curtos estendendo os caminhos mais curtos aresta por aresta (cujo tempo de execução é Theta(n⁴)).

SLOW-ALL-PAIRS-SHORTEST-PATHS(W)

1 n <- linhas[L]

2 L⁽¹⁾ <- W

3 for m <- 2 to n - 1

4   do L^(m) <- EXTEND-SHORTEST-PATHS(L^(m-1), W)

5 return L^{(n - 1)}

Figura 25.1 Um grafo orientado e a sequência de matrizes L^(m) calculada por SLOW-ALL-PAIRS-SHORTEST-PATHS.

Contudo, não é necessário o cálculo de todas as matrizes L^(m). O objetivo é calcular a matriz L^(n-1). Graças a propriedade de associatividade do procedimento EXTEND-SHORTEST-PATHS, pode-se calcular L^(n-1) apenas com Teto(lg(n-1)) produtos de matrizes. O procedimento abaixo emprega então essa importante propriedade denominada elevação ao quadrado repetida.

FASTER-ALL-PAIRS-SHORTEST-PATHS(W)

1 n <- linhas[L]

2 L⁽¹⁾ <- W

3 m <- 1

4 while  m < n – 1

5   do L^(m) <- EXTEND-SHORTEST-PATHS(L^(m), L^(m))

6     m <- 2m

7 return L^(m)

Em cada iteração do loop while das linhas 4 a 6, calcula-se L^(2m) = (L^(2m))², começando com m = 1. No valor de cada iteração, o valor de m é duplicado. A iteração final calcula L^(n-1) calculando na verdade L^(2m) para algum n-1 <= 2m < 2n-2. O tempo de execução total desse algoritmo é Theta(n³ lg n).

O algoritmo de Floyd-Warshall também utiliza uma formulação de programação dinâmica (assim como no caso dos algoritmos de todos os pares baseados na multiplicação de matrizes). Porém, é importante salientar que esta caracterização é diferente da que foi apresentada anteriormente.

FLOYD-WARSHALL(W)

1 n <- linhas[L]

2 D(0) <- W

3 for k <- 1 to n

4   do for i <- 1 to n

5      do for j <- 1 to n

6        do d_ij^(k) <-min(d_ij^(k-1), d_ik^(k-1)+ d_kj^(k-1))

7   return D⁽ⁿ⁾

Para um detalhamento maior, consulte o livro-texto na pág. 497-498. O tempo de execução do algoritmo de Floyd-Warshall é determinado pelos loops for triplamente aninhados das linhas 3 a 6. Cada execução da linha 6 demora o tempo O(1). Portanto, o algoritmo é executado no tempo Theta(n³).

Figura 25.4 A sequência de matrizes D^(k) calculada pelo algoritmo de Floyd-Warshall para o grafo da Figura 25.1

O objetivo é, dado um grafo orientado G = (V,E) com o conjunto de vértices V = {1,2,...,n}, descobrir se existe um caminho em G desde i até j para todos os pares de vértices i,j ∈ V. O fecho transitivo de G é definido como o grafo G^* = (V, E^*), onde

E^* = {(i,j) : existe um caminho desde o vértice i até o vértice j em G}.

TRANSITIVE-CLOSURE(G)

1 n <- |V[G]|

2 for i <- 1 to n

3   do for j <- 1 to n

4     do if i = j or (i,j) ∈ E[G]

5        then t_ij⁽⁰⁾ <- 1

6        else t_ij⁽⁰⁾ <- 0

7   for k <- 1 to n

8    do for i <- 1 to n

9      do for j <- 1 to n

10      do t_ij^(k) <- t_ij^(k-1) ∨ (t_ij^(k) ∧ t_ij^(k))

11 return T⁽ⁿ⁾

O algoritmo acima envolve a substituição das operações aritméticas min e + no algoritmo de Floyd-Warshall pelas operações lógicas ∨ (OU lógico) e ∧ (E lógico). Para i,j,k = 1,2,...,n, definimos t_ij^(k) como 1 se existe um caminho no grafo G desde o vértice i até o vértice j com todos os vértices intermediários no conjunto {1,2,...,k}e 0 em caso contrário. Construímos o fecho transitivo G^* = (V, E^*) inserindo a aresta (i,j) em E^* se, e somente se t_ij⁽ⁿ⁾ = 1.

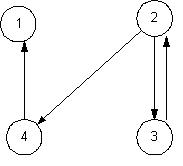
Figura 25.5. Um grafo orientado e as matrizes T^(k) calculadas pelo algoritmo de fecho transitivo