MO417
Ata de Aula

Assunto : Fluxo Máximo 2 ( Capítulo 26 )

Data: 13/06/2003
Redator: Guilherme Mundim Torres

      O método de Ford-Fulkerson consiste em procurar por um caminho aumentante p e aumentar o fluxo f de cada aresta do caminho aumentante levando em consideração a capacidade residual das mesmas. Devemos nos atentar para o fato de que se dois vértices, u e v, não estiverem conectados por uma aresta, deve-se considerar que o fluxo f[u,v] é igual a zero.

O algoritmo Ford-Fulkerson abaixo consiste numa extensão do pseudocódigo Ford-Fulkerson-Method visto na aula anterior. Ele termina quando não for mais possível encontrar um caminho aumentante na rede residual.

FORD-FULKERSON(G,s,t)
1 for cada aresta (u,v) <- E[G]
2   do f[u,v] <- 0
3        f[v,u] <- 0
4 while existir um caminho p de s até t na rede residual Gf
5     do cf(p) <- min{cf(u,v) : (u,v) está em p}
6          for cada aresta (u,v) em p
7               do f[u,v] <- f[u,v] + cf(p)
8                   f[v,u] <- (-f[u,v])

O tempo de execução do mesmo depende da maneira como se determina o caminho aumentante. Em alguns casos, o algoritmo pode nunca terminar ( se as arestas forem números irracionais ) ou demorar muito tempo até encontrar o valor de fluxo máximo. Para que o algoritmo seja executado em tempo polinomial, deve ser utilizada a Busca em Largura para se determinar o caminho aumentante.

Se as capacidades das arestas consistirem em números inteiros, no pior caso o caminho será aumentando de uma em uma unidade a cada iteração. O tempo de execução do algoritmo será O( E | f* | ), onde o f* corresponde ao valor do fluxo máximo encontrado pelo algoritmo.

A implementação do algoritmo deve utilizar lista de adjacências para representar a rede G = (V,E). Assim, o tempo para se encontrar um caminho na rede residual será O (E) . Como o loop while da linha 4 é executado em tempo O (E) e ele será executado no máximo | f* | vezes ( o valor do fluxo aumenta pelo menos uma unidade para cada iteração ) chega-se a um tempo de execução total igual a O( E | f* | ).

O algoritmo de Edmonds-Karp consegue melhorar o limite do algoritmo de Ford-Fulkerson escolhendo sempre a distância do caminho mais curto desde s até t na rede residual.

Durante a aula foi explicado o conceito de aresta crítica : uma aresta (u,v) em uma rede residual Gf é crítica em um caminho aumentante quando a capacidade residual do caminho equivale à capacidade residual da aresta (u,v). Uma aresta crítica pode ser comparada a um "gargalo" , pois é a menor do caminho.

Como cada iteração do algoritmo de Ford-Fulkerson leva tempo O(E) quado se utiliza Busca em Largura na procura do caminho aumentante, o algoritmo de Edmonds-Karp pode ser executado em tempo O(VE^2).

Considerando um grafo G = (V, E), um emparelhamento consiste em um subconjunto de arestas M contido em E, tais que, para todo vértice v pertencente a V, no máximo uma aresta de M é incidente sobre v. Dessa forma, o emparelhamento bipartido máximo consiste numa escolha de arestas que não se tocam, em grafos bipartidos.

Pode-se visualizar uma aplicação de emparelhamento bipartido máximo à partir do problema da linha de produção, que considera uma correspondência de um conjunto L de máquinas com um conjunto R de tarefas a serem executadas simultaneamente. A presença de uma aresta (u,v) significa que uma determinada máquina u pertencente a L é capaz de executar uma tarefa v pertencente a R. A resolução do problema deverá fornecer trabalho para o maior número de máquinas possível.

O problema de se encontrar um emparelhamento máximo em um grafo bipartido não orientado pode ser resolvido pelo método de Ford-Fulkerson, em tempo polinomial em | V | e | E | : O (VE). Para tal, deve ser construído um fluxo em rede onde os fluxos são equivalentes aos emparelhamentos. A figura abaixo ilustra o problema :

Ao fluxo de rede correspondente ao grafo bipartido são adicionados dois vértices, s e t (em negrito). Em seguida o vértice s é conectado a todos os vértices L e todos os vértices R são conectados ao vértice t. Cada aresta tem capacidade unitária. As arestas sombreadas têm um fluxo igual a 1 e as arestas restantes não conduzem nenhum fluxo. As arestas em negrito de L até R compõe uma correspondência máxima do grafo bipartido. Neste caso, tem-se M = 3.

Em sala de aula foi apresentado um exemplo ilustrando um caso em que uma aresta poderia deixar de participar de um emparelhamento, como pode ser visto a seguir :

Considere o grafo abaixo :

O primeiro caminho aumentante encontrado foi s -> b -> c -> t, marcado em vermelho na próxima figura. A aresta participante do emparelhamento é a aresta (b,c). As arestas (s,b),(b,c),(c,t) terão suas capacidades residuais iguais a zero.

Na figura abaixo, o novo caminho aumentante está representado pelas arestas vermelhas.

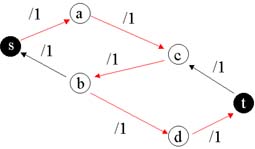
Finalmente, observe que na figura abaixo não é mais possível estabelecer um caminho aumentante. Verifique que as arestas (a,c) e (b,d) são as únicas participantes do emparelhamento, sendo que a aresta (b,c) deixou de participar do emparelhamento, caracterizando o emparelhamento máximo.