Hierarquia booleana

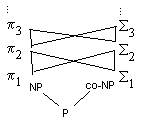
No primeiro nível da hierarquia booleana encontram-se as classes NP e co-NP (classe de complexidade de tempo que está sendo estudada). A hierarquia vai crescendo até o infinito. Se resolver algum problema na hierarquia, ela colapsa dali para baixo.

Figura 4: Hierarquia booleana

Existe também a classe de complexidade de espaço, que tem problemas mais difíceis. Essa classe contém os problemas que podem ser resolvidos usando espaço polinomial. Esses problemas permitem uma liberdade muito maior. Por exemplo, o jogo de xadrez é um problema que pode ser resolvido usando um espaço polinomial, mas não pode ser resolvido em tempo polinomial (ver história da nomenclatura da classe de complexidade de tempo).

PSPACE é a classe de problemas que podem ser resolvidos usando espaço polinomial. Existem também os problemas NPSPACE-completo. Foi provado que PSPACE= NPSPACE. Existem problemas que não estão em NPSPACE, ou seja, existem problemas que não se pode resolver usando espaço polinomial.

O problema da parada de Turing é um deles. Ele fica acima de todos os problemas, pois nem existe algoritmo para ele.