MO417 -

Ata de exercícios

Ordenação em tempo linear

Ata - Resolução do exercícios do dia 21/03/2003
Dia da digitação desta ata: 22/03/2003
Redator: Ricardo Luís Lachi 972929


Organização desta ata:

    1. Proposta de resolução dos exercícios
    2. Lemas ou algoritmos utilizados nos exercícios


1. Proposta de resolução dos exercícios
8.3-4 Mostre como ordenar n inteiros no intervalo de 0 a   no tempo O(n).
        . Resolução:
    A solução proposta foi utilizar o algoritmo do RADIX-SORT com base no Lemma 8.4 da página 139 e no fato de que qualquer número na faixa de valores [0..n - 1] pode ser sempre representado na base 2 utilizando-se lg n bits.

    Logo, como é dito no exercício que o maior inteiro existente no vetor tem valor , então esse inteiro pode ser representado com bits = 2 * lg n bits.

    Substituindo esse valor na fórmula no lugar de b no Lemma 8.4 obtemos:

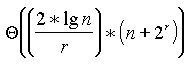
    Escolhendo o valor de r como sendo  porque essa é a escolha de r que fornece o melhor tempo dentro de um fator constante (ver explicação deste fato na página 139 do capítulo 8), obtemos:

    Simplificando:

    Resultando em:

    Conclusão: com isso comprovou-se que a utilização do RADIX-SORT é capaz de ordenar corretamente os n inteiros no tempo . Completando: se um algoritmo é significa que é também e O(n). Logo, o resultado calculado comprova o que é pedido no exercício, isto é, que o tempo seja O(n).


8.4-2 Qual é o tempo de execução do pior caso para o algoritmo de bucket sort ? Que alteração simples no algoritmo preserva seu tempo de execução esperado linear e torna seu tempo de execução no pior caso igual a O(n * lg(n)) ?
        . Resolução:
    Primeira parte da questão)
      O pior caso ocorre quando todos os elementos do vetor estão ordenados decrescentemente e são colocados em um mesmo balde.

      Isso acaba fazendo com que o algoritmo do bucket sort acabe gastando , uma vez que o algoritmo INSERTION-SORT (que compõe o bucket sort) vai levar na ordenação desse balde.

    Segunda parte da questão)
      Trocar o algoritmo de ordenação INSERTION-SORT componente do algoritmo bucket sort por um outro cujo tempo de execução do pior caso seja O(n * lg n), como por exemplo, o algoritmo Heapsort.


Problema 8-2 Vamos supor que temos um arranjo de n registros de dados para ordenar e que a chave de cada registro tem o valor 0 ou 1. Um algoritmo para ordenar tal conjunto de registros poderia ter algum subconjunto das três características desejáveis a seguir:
    1. O algoritmo é executado no tempo O(n).
    2. O algoritmo é estável.
    3. O algoritmo ordena localmente, sem utilizar mais que uma quantidade constante de espaço de armazenamento além do arranjo original.
                                      . a. Dê um algoritmo que satisfaça aos critérios 1 e 2 anteriores.
    O algoritmo proposto como resposta foi o COUNTING-SORT.

b. Dê um algoritmo que satisfaça aos critérios 1 e 3 anteriores.
    A algoritmo proposto como resposta foi o PARTITION da página 118 pois as chaves são só 0's e 1's.
c. Dê um algoritmo que satisfaça aos critérios 2 e 3 anteriores.
    O algoritmo proposto como resposta foi o INSERTION-SORT.
d. Algum dos seus algoritmos de ordenação das partes (a)-(c) pode ser usado para ordenar n registros com chaves de b bits usando radix sort no tempo O(bn) ? Explique como ou por que não.
    O algoritmo da parte (a). Isso porque o radix-sort, para funcionar corretamente, necessita de um algoritmo de ordenação estável no seu núcleo que é o caso do counting-sort. Além disso, o tempo de execução do counting-sort é O(n) para inteiros cujo valores sejam limitados por alguma constante (no caso, é dito que são limitados por b bits). Logo o counting-sort apresentado como resposta para o item (a), preenche as condições pedidas neste item..


2. Lemas ou algoritmos referenciados nos exercícios
Lema 8.4 Dados n números de b bits e qualquer inteiro positivo r <= b, RADIX-SORT ordena corretamente esses números no tempo
               .
Algoritmo Bucket sort
    BUCKET-SORT(A)
    1 n = comprimento[A]
    2 for i = 1 to n
    3    do inserir A[i] na lista   
    4 for i = 0 to n - 1
    5    do ordenar lista B[i] com ordenação por inserção
    6 concatenar as listas B[0], B[1], ..., B[n-1] juntas em ordem
Algoritmo Insertion sort
    INSERTION-SORT(A)
    1 for j = 2 to comprimento[A]
    2    do chave = A[j]
    3        Inserir A[j] na sequência ordenada A[1..j-1].
    4        i = j - 1
    5        while i > 0 e A[i] > chave
    6           do A[i + 1] = A[i]
    7                 i = i - 1
    8        A[i + 1] = chave
Algoritmo Partition
    PARTITION(A, p, r)
    1 x = A[r]
    2 i = p - 1
    3 for j = p to r - 1
    4     do if A[j] <= x
    5              then i = i + 1
    6                       trocar A[i] = A[j]
    7 trocar A[i+1] com A[r]
    8 return i + 1
Algoritmo radix sort
    RADIX-SORT(A, d)
    1 for i = 1 to d
    2 do usar uma ordenação estável para ordenar o arranjo A sobre o dígito i