MO417
Ata de Exercícios

Data: 26/03/2003
Redator: Guilherme Mundim Torres

Capítulo 9: Medianas e estatísticas de ordem

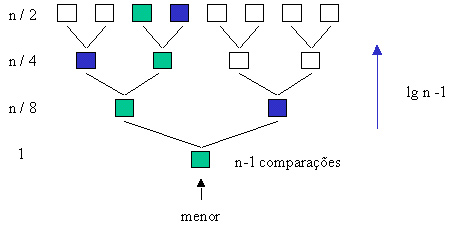
      O algoritmo deverá comparar todos os números aos pares. Como somente o menor de cada par poderá ser o menor de todos os pares, tem-se que o problema é sucessivamente reduzido pela metade. Prosegue-se com esta operação até encontrar o menor número.

     Serão necessárias n-1 comparações, desde que consideremos que o percurso possa ser representado por uma árvore binária que possui n-1 nós internos, sendo que cada um deles corresponde a uma comparação. A figura abaixo ajuda a ilustrar a execução do algoritmo. Os elementos de cor verde ganharam na comparação do menor de cada par no sentido de cima para baixo, até que foi encontrado o menor número (a raíz da árvore).

     Agora a mesma árvore será utilizada na localização do 2° menor elemento. Para encontrá-lo, deve-se percorrer o caminho na árvore utilizado para encontrar o 1° menor no sentido inverso, já que certamente o 2° menor foi comparado com o 1° menor em algum momento. Os elementos de cor azul ilustram o caminho inverso a ser percorrido, sendo que um deles será o 2° menor elemento. Este processo levará teto(lg n) -1 comparações, pois percorrerá a altura da árvore - 1 (a raiz).

     Assim, o número total de comparações é de : n-1 + teto(lg n) -1 = n + teto(lg n) - 2

Parte1) Verificação do funcionamento do algoritmo em tempo linear caso os elementos de entrada sejam divididos em grupos de 7.

# Primeiramente calcula-se um limite inferior sobre o número de elementos que são maiores que o elemento de particionamento x :

4*(teto(1/2*teto(n/7))-2) <= 2n/7 - 8

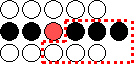
# Através da ilustração abaixo podemos observar que pelo menos metade das medianas encontradas é maior que a mediana de medianas x. Assim, pelo menos metade dos (teto(n/7)) grupos contribui com 4 elementos maiores que x (representados pela área tracejada na figura abaixo), com exceção do grupo que tem menos de 7 elementos caso 7 não seja um divisor exato para n, e pelo grupo que contém o próprio x.

# Para saber sobre quantos elementos o SELECT será chamado recursivamente no pior caso, devemos calcular o complemento do resultado obtido na inequação encontrada no primeiro passo da resolução do problema:

n - ((2n/7) - 8) = 5n/7 + 8

# A recorrência para o tempo de execução do pior caso T(n) do algoritmo SELECT:

T(n) = T(n/7) + T(5n/7 + 8) + O(n)

# Mostrar que T(n) <= cn, seguindo os passos das p. 153-154 do livro:

T(n) <= cteto(n/7) + c(5n/7 + 8 ) + an

        <= cn/7 + c + 5cn/7 + 8c + an

          = 6cn/7 + 9c + an

          = cn + ( - cn/7 + 9c + an )

# Para provar que T(n) <= cn :

- cn/7 + 9c + an <= 0

cn/7 - 9c >= an

c >= 7an/(n-63)

# Considerando n >= 126, tem-se :

c >= 7a(126/(126-63))

c >= 14a

#Portanto, se c >= 14a, T(n) <= cn; então T(n) = O(n).

Parte2) Verificação do funcionamento do algoritmo em tempo linear caso os elementos de entrada sejam divididos em grupos de 3.

# Primeiramente calcula-se um limite inferior sobre o número de elementos que são maiores que o elemento de particionamento x :

2*(teto(1/2*teto(n/3))-2) <= n/3 - 4

# Através da ilustração abaixo podemos observar que pelo menos metade das medianas encontradas é maior que a mediana de medianas x. Assim, pelo menos metade dos (teto(n/3)) grupos contribui com 2 elementos maiores que x, com exceção do grupo que tem menos de 3 elementos caso 3 não seja um divisor exato para n, e pelo grupo que contém o próprio x.

# Para saber sobre quantos elementos o SELECT será chamado recursivamente no pior caso, devemos calcular o complemento do resultado obtido na inequação encontrada no primeiro passo da resolução do problema:

n - ((n/3) - 4) = 2n/3 + 4

# Particionando em 3 elementos, a recorrência pode ser representada por :

T(n) = T(n/3) + T(2n/3 + 4) + f(n), onde f(n) = Theta(n).

# Queremos mostrar que T(n) >= cnlg(n).

# Primeiramente, sabemos que existem a e b positivos tais que an <= f(n) <= bn para todo n>=1. Assim, a recorrência pode ser reescrita como :

T(n) >= T(n/3) + T(2n/3 + 4) + an.

# Agora, deve-se utilizar o método da substituição como tentativa de encontrar a prova por indução de que
T(n) >= cnlg(n), a partir, é claro, de um certo n0, tendo ainda que escolher c.

# Agindo de forma semelhante ao livro nas páginas 153 e 154, porém com >= em lugar de <=, temos:

T(n) = T(n/3) + T(2n/3 + 4) + an
     >= c(n/3)lg(n/3) + c(2n/3 + 4)lg(2n/3 + 4) + an
     >= c(n/3)lg(n/3) + c(2n/3)lg(2n/3) + an
      = c(n/3)(lg(n) + lg(1/3)) + c(2n/3)(lg(n) + lg(2/3)) + an
      = c(n/3)lg(n) + c(n/3)lg(1/3) + c(2n/3)lg(n) + c(2n/3)lg(2/3)) + an
      = cnlg(n) + cn((1/3)lg(1/3) + (2/3)lg(2/3)) + an
      = cnlg(n) + n( a + c((1/3)lg(1/3) + (2/3)lg(2/3)).

# Como a expressão (1/3)lg(1/3) + (2/3)lg(2/3) é negativa, não se pode simplesmente concluir direto que a última linha é >= cnlg(n). Porém, o termo an vem em nosso auxílio, e tudo que precisamos fazer é escolher c (positivo, claro), tal que:

a + c((1/3)lg(1/3) + (2/3)lg(2/3)) >= 0

# ou seja,

c <= a/(-(1/3)lg(1/3) - (2/3)lg(2/3))

# o que é possível, pois o lado direito é positivo. Não precisamos de hipóteses sobre n, logo, podemos tomar n0 = 1.

#Assim, fica demonstrado que SELECT não será executado em tempo linear se forem usados grupos de 3 elementos.

Seção problemas (pág. 155)   

a. Classifique os números e liste os i maiores.

Algoritmo utilizado para a classificação: Merge Sort (O(n lg n))

Tempo de execução : O(n lg n)

* A complexidade da listagem é O(i), e pode ser ignorada por ser menor que a complexidade da classificação.

b. Construa uma fila de prioridade a partir dos números e chame EXTRACT-MAX i vezes.

Algoritmo utilizado para construção da fila: Build Max Heap (O(n))

i chamadas a EXTRACT-MAX: O(i lg n)

Tempo de execução : O(n + i lgn)


c. Use um algoritmo de estatística de ordem para localizar o i-ésimo maior número, particionar e ordenar os i maiores números.

Para localizar o i-ésimo maior número, o tempo de execução é O(n) através do SELECT. Para particionar, o tempo é também O(n) com o algoritmo PARTITION. Para ordenar os i maiores números, pode-se utilizar o MERGE SORT que leva O(i lg i) .

Tempo de execução : O(n + i lgi)