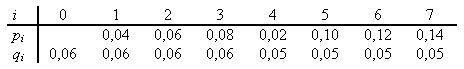MO417 - Ata de
exercícios (Programação Dinâmica 2)
Ata – Aula do dia 09/04/2003
Redatora: Daniele Constant Guimarães – ra: 012108
Organização :
1. Proposta de resolução dos exercícios
2. Algoritmos utilizados nos exercícios
1. Proposta de resolução dos exercícios
15.3-5 - Como está
enunciado, em programação dinâmica primeiro resolvemos
os subproblemas e depois escolhemos qual deles utilizar em uma solução
ótima para o problema. A professora Capulet afirma que nem sempre
é necessário resolver todos os subproblemas a fim de encontrar
uma solução ótima. Ela sugere que uma solução
ótima para o problema de multiplicação de cadeias
de matrizes pode ser encontrada escolhendo-se sempre a matriz A
k
na qual será dividido o subproduto A
iA
i+1
... A
j (selecionando-se
k para minimizar a quantidade
pi-1pkpj)
antes de resolver os subproblemas. Encontre uma instância
do problema de multiplicação de cadeias de matrizes para
a qual essa abordagem gulosa produz uma solução não
ótima.
Resolução:
O exemplo abaixo dá um total de operações
maior que a ótima quando se usa o método da profa. Capulet.
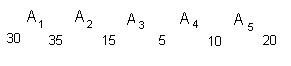
- Fazeendo Ak = A3, as subcadeias de
matrizes serão:
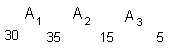 e
e 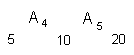
- Fazendo Ak = A2, para a primeira
subcadeia, teremos:
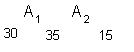 e
e 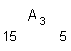
Segundo o método da profa. Capulet, a colocação
ótima dos parênteses seria:
((A1A2)A3)(A4A5),
onde:
- A1A2 executam um total de 30*35*15
= 15750 operações,
- (A1A2)A3 executam
um total de 30*15*5 = 2250 operações,
- A4A5 executam um total de 5*10*20
= 1000 operações,
Totalizando 15750+2250+1000 = 22000 operações
A solução ótima encontrada
usando a multiplicação de cadeias de matrizes tradicional
executa um total de 11875 operações e resulta
na colocação ótima dos parênteses (A1(A2A3)(A4A5).
OBS: Essa colocação ótima
dos parênteses no método tradicional foi tirada de um exemplo
do livro texto adotado. (pags 266 a 271)
15.4-1 - Determine
uma LCS de <1, 0, 0, 1, 0, 1, 0, 1> e <0, 1, 0, 1, 1, 0, 1,
1, 0>.
Resolução:
Tabela LCS-LENGHT construída a partir
do procedimento LCS_LENGHT proposto na página 283 do livro texto (transcrito
na sessão 2 desta ata) é mostrada abaixo:
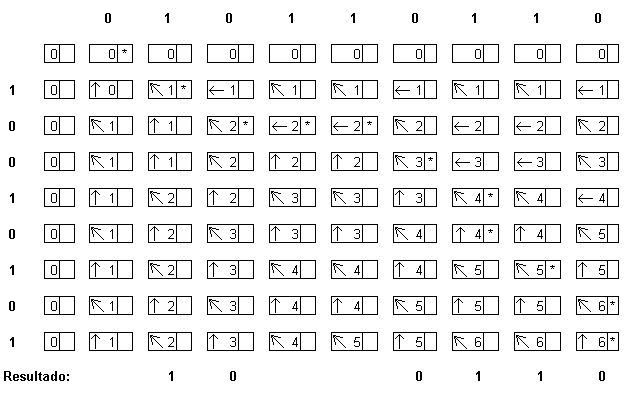
A solução encontrada a partir dessa
tabela foi {1, 0, 0, 1, 1, 0}. Mas ela não é a única
possível. Existem pelo menos mais três: {1, 0, 1, 0, 1, 0},
{0, 1,0 ,1 ,0, 1} e {0, 0, 1, 0, 1, 0}. Essa solução foi
encontrada iniciando a busca em b[8, 9] (b[m, n]) e
percorrendo a tabela seguindo as setas. Sempre que uma seta  for encontrada na entrada b[i, j] implica que xi
= yj é um elemento da LCS.
for encontrada na entrada b[i, j] implica que xi
= yj é um elemento da LCS.
15.5-2 - Determine o
custo e a estrutura de uma árvore de pesquisa binária ótima
para um conjunto de n=7 chaves com as seguintes probabilidades:
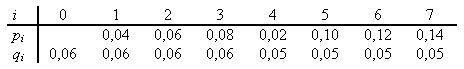
Resolução:
As tabelas OPTIMAL-BST construídas a partir do procedimento OPTIMAL_BST
da página 289 do livro(transcrito na sessão 2 desta ata) são
mostradas abaixo:
Tabela que armazena os valores e[i, j] dos custos esperados
da pesquisa na árvore binária ótima.
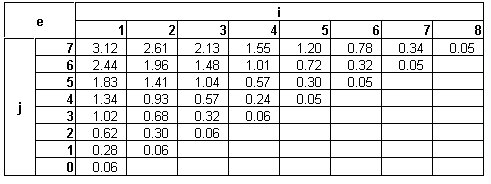
Tabela que armazena as somas w[i, j] de todas as probabilidades
na subárvore.
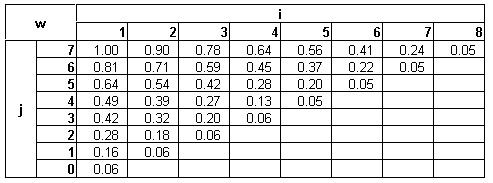
Tabela que armazena as raízes de uma árvore de pesquisa binária
ótima.
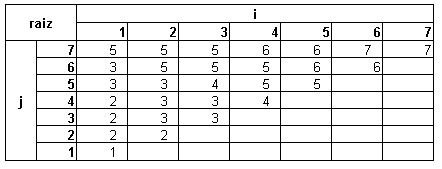
O custo da árvore de pesquisa binária ótima
é: 3,12
E sua estrutura é:
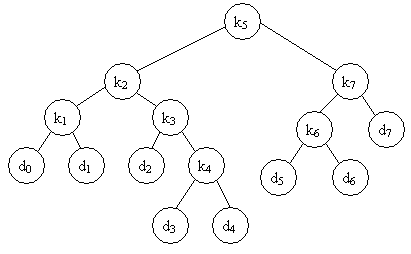
2. Algoritmos utilizados nos exercícios
Exercício 15.4-1
LCS-LENGHT(X, Y)
1
|
m  comprimento [X]
comprimento [X]
|
2
|
n  comprimento [Y]
comprimento [Y]
|
3
|
for i  1 to m
1 to m
|
4
|
do
c[i, 0]  0
0
|
5
|
for j  0 to n
0 to n
|
6
|
do
c[0, j]  0
0
|
7
|
for i  1 to m
1 to m
|
8
|
do
for j  1 to n
1 to n
|
9
|
do if xi = yj
|
10
|
then c[i, j]  c[i-1, j-1] + 1
c[i-1, j-1] + 1
|
11
|
b[i, j]  "
"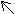 "
"
|
12
|
else if c[i-1, j] >= c[i,
j-1]
|
13
|
then c[i, j]  c[i-1, j]
c[i-1, j]
|
14
|
b[i,
j]  "
"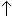 "
"
|
15
|
else c[i, j]  c[i, j-1]
c[i, j-1]
|
16
|
b[i,
j]  "
" "
"
|
17
|
return c e b
|
O procedimento LCS_LENGHT recebe como entrada duas sequências
X= < x1, x2, ..., xm> e Y= <y1,
y2, ...,yn>. Ele armazena os valores c[i,
j] em uma tabela c[0..m, 0..n] cujas entradas são
calculadas em ordem de linha principal. Ele também mantém a
tabela b[1..m, 1..n] para simplificar a construção
de uma solução ótima. Intuitivamente, b[i,
j] aponta para a entrada da tabela correspondente à solução
ótima do subproblema escolhido ao calculart c[i, j].
O procedimento retorna as tabelas b e c; c[m, n]
contém o comprimento de uma LCS de X e Y.
Exercício 15.5-2
OPTIMAL-BST(p, q, n)
1
|
for i  1 to n+1
1 to n+1
|
2
|
do e[i,
i-1]  qi-1
qi-1
|
3
|
w[i, i-1]  qi-1
qi-1
|
4
|
for l  1 to n
1 to n
|
5
|
do for i  1 to n - l + 1
1 to n - l + 1
|
6
|
do j  i + l - 1
i + l - 1
|
7
|
e[i, j] 
|
8
|
w[i, j]  w[i, j-1] + pi+
qj
w[i, j-1] + pi+
qj
|
9
|
for r  i to j
i to j
|
10
|
do t  e[i, r-1] + e[r+1,
j] + w[i, j]
e[i, r-1] + e[r+1,
j] + w[i, j] |
11
|
if t < e[i, j]
|
12
|
then e[i,
j]  t
t
|
13
|
raiz[i, j]  r
r
|
14
|
return e e raiz
|
O procedimento OPTIMAL_BST recebe como entrada as probalidades
p1, ..., pn e q0, ...,
qn e o tamanho n e retorna as tabelas e e
raiz.
Esse procedimento armazena os e[i, j] valores dos custos esperados
da pesquisa na árvore de pesquisa binária ótima em uma
tabela e[1..n+1, 0 ..n]. O primeiro índice vai
até n+1 para que se tenha uma subárvore contendo apenas
a chave fictícia dn. Para isso, deve-se calcular
e armazenar e[n+1, n]. O segundo índice deve começar
de 0 para que se tenha uma subárvore contendo apenas a chave fictícia
d0. Para isso, deve-se calcular e armazenar e[1,
0]. Somente as entradas e[i, j] para j >= i
- 1 serão usadas. Será usada também uma tabela raiz[i,
j] para registrar a raiz da subárvore que contém as chaves
ki, ..., kj. Só utiliza as entradas onde
1<= i <= j <= n. Para manter a eficiência
será usada uma tabela auxiliar w[1..n+1, 0..n].
Os valores w[i, j] serão calculados de acordo com as fórmulas
abaixo:
w[i, i-1] = qi-1, para 1 <=
i <= n.
w[i, j] = w[i, i-1] + pj
+ qj, para j >= i.
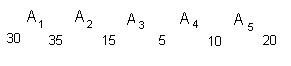
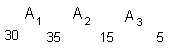 e
e 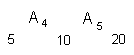
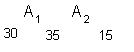 e
e