Ata de Exercícios do dia 16/04/2003
Referente ao capítulo 16 (Tópicos 16.1 e 16.2)
Professor: João Meidanis
Redator: Thiago Alves da Silva
2. Algoritmo utilizado na resolução
3. Referências Bibliográficas
Solução apresentada:
Abordagem de selecionar a atividade de menor duração - (Apresentada pelo aluno José Augusto)
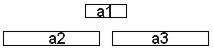
Segundo essa abordagem, apenas a atividade a1 seria selecionada.
Segundo a abordagem gulosa vista no livro, (término mais antigo),
o subconjunto {a2, a3} é maior.
Abordagem de selecionar a atividade que se superpõe ao menor número de outras atividades - (Apresentada pelo aluno Patrick)
Observação: a interpretação usada aqui é a de que o número de superposições é calculado apenas uma vez para todas as atividades no início e nunca mais atualizado.
Segunda essa abordagem, apenas as atividades a2, a5 e
a9
seriam selecionadas. A abordagem gulosa vista no livro (término
mais antigo), produz o subconjunto {a2, a3, a4, a5}, que nesse caso é
maior.
Abordagem de selecionar a atividade com o tempo de início mais antigo - (Apresentada pela aluna Camila)
Segundo essa abordagem, apenas a atividade a1 seria selecionada.
Mas, segundo a abordagem gulosa vista no livro, o subconjunto {a2, a3}
é maior.
Solução apresentada pelo aluno Guilherme:
O espaço de armazenamento será uma tabela c de tamanho n x w, onde n é o número de itens e w o peso de cada item.
A entrada c[i,w] indica o valor da solução para os itens 1,..,i e peso máximo w, onde w varia de 0 até W. A seguinte recorrência denota como será preenchido o espaço de armazenamento.
| 0
se i = 0 ou w = 0
c[i,w] = { c[i-1,w]
se wi > w
| max (vi + c[i-1, w - wi], c[i-1, w])
se i > 0 e w >= wi
Onde: vi representa o valor do i-ésimo elemento e
wi o peso do i-ésimo elemento.
Algoritmo e prova apresentados pelo aluno André:
| MAXIMO(S,p)
1 ordena-peso(S) // ordem crescente de pesos 2 n <- comprimento[S] 3 F <- Ø 4 i <- 1 5 while ( i <= n and p > peso(S[i]) ) 6 F <- F U S[i] 7 p <- p - peso(S[i]) 8 return F |
Algoritmo proposto pelo aluno Alexandro:
Entrada: X = {x1, x2, ..., xn} e n
Saída: S -> conjunto dos pontos iniciais
| MENORINT(X,n) {
1 heapsort(X); // ordem crescente 2 ponto = 1; 3 S = Ø; 4 while ( ponto <= n ) { 5 inserir = X[ponto]; 6 S = S U inserir; 7 while ( ponto <= n and X[ponto] <= inserir+1) 8 ponto++; 9 } 10 } |
Dado x1um ponto inicial da reta.
Suponha por contradição que existe um segmento contendo
x1 que contenha mais pontos que o segmento que inicia em x1.
O segmento não pode começar depois de x1. Se este
segmento inicia antes de x1, ele não conterá mais
pontos antes de x1 e conterá, depois de x1,
um número de pontos menor ou igual à solução
iniciada em x1. Portanto, é um absurdo a existência
deste segmento.
O professor concluiu dizendo que o algoritmo possui complexidade O(n
lg n), devido a chamada 'heapsort' na linha 1.
.
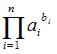Forneça um algoritmo que maximize sua recompensa. Prove que seu
algoritmo maximiza a recompensa e enuncie seu tempo de execução.
Solução proposta pelo aluno André:
Tomemos um exemplo onde os conjuntos A e B possuem três elementos cada. Isto resulta na multiplicação:
Podemos interpretar a potência a elavada a b como um produtório de a, b vezes. Desta forma, o produtório acima seria equivalente a:
O produtório pode ser também expresso como multiplicações entre bases ai (sem expoente) que aparecem bi vezes:
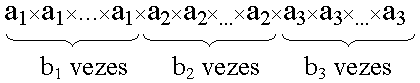
Chamaremos esta representação de R.
Agora iremos partir da escolha de um produtório onde os elementos do conjunto A e do conjunto B estão classificados em ordem crescente de valores, de tal modo que ai <= a(i+1) e bi <= b{i+1). Chamaremos esta solução de S, declarando que ela maximiza o produtório.
Para provar isto vamos supor, por contradição, que exista uma solução S' cujo resultado do produtório seja maior.
Tomemos am como o elemento de maior valor do conjunto A e bm como o elemento de maior valor do conjunto B (em ambos os casos, caso haja mais de um elemento de maior valor será considerado o último na sequência de índices do conjunto). Considerando que o algoritmo de ordenação para solução S é estável:
Na solução S, am possui um
expoente bm.
Na solução S', am possui
um expoente bx cujo valor é menor ou
igual a bm.
Se bm = bx o
número de vezes que am aparece no produtório
da representação R é igual para as duas soluções.
Se bm > bx
o número de vezes que am aparece no
produtório da representação R para a solução
S será maior que em S'.
Como o número de termos na representação R é sempre o mesmo, a redução do número de vezes que aparece am, implicará no aumento do número de vezes que aparece um ax, cujo valor é menor ou igual a am. Isto significa em qualquer solução que maximize o valor do produtório, am tem que estar associado a um bx = bm.
Por este motivo, vamos supor, sem perda de generalidade, que am esteja associado a bm em S', pois qualquer outro bx escolhido teria valor igual a bm, o que não afeta o resultado. Isto significa que este termo (am elevado a bm) é igual em S e S'. Vamos então remover am e bm, já que são iguais em ambas as soluções, e analisar os subconjuntos de A e B sem os mesmos.
A mesma propriedade do maior elemento, analisado até então, se aplicará neste subcojunto, e assim sucessivamente até que sobre apenas um ax elevado a bx em na solução S e um ay elevado a by em S'. Como em todos os termos, removidos nas etapas anteriores, os valores de a sempre foram iguais em S e S', bem como os valores de b, então ax=ay e bx=by.
Isto significa que o resultado do produtório de S' será necessariamente igual ao de S, em outras palavras, é um absurdo a existência de um S' cujo resultado do produtório seja maior que S.
Provamos então por absurdo que S maximiza o valor do produtório.
| HEAPSORT(A)
1 BUILD-MAX-HEAP(A) 2 for i <- comprimento[A] downto 2 3 do trocar A[1] <-> A[i] 4 tamanho-do-heap[A] <- tamanho-do-heap[a]-1 5 MAX-HEAPIFY(A,1) |