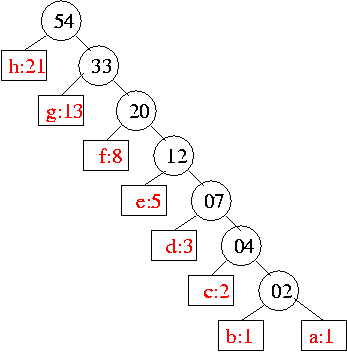
Percorrendo essa árvore a partir da raiz é possível saber qual o código binário ótimo para cada letra, de acordo com sua freqüência:
| h |
0 |
| g |
10 |
| f |
110 |
| e |
1110 |
| d |
11110 |
| c |
111110 |
| b |
1111110 |
| a |
1111111 |
0 - caminho esquerdo da árvore
(nesta implementação)
1 - caminho direito da árvore (nesta implementação)- PROVA PARA UM CASO GERAL:
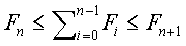
Como vemos, a prova se divide em duas etapas: a primeira mostra que um número de Fibonacci é sempre <= a soma de todos os seus antecessores:
Primeira parte:
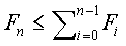 :
: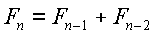 e
e 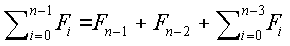
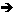
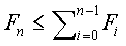
Segunda parte:
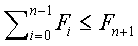 :
:De acordo com o Lema 20.2 do livro Algoritmos de Thomas H. Cormen, que diz que dada uma série de números de Fibonacci (Fn), onde n é a ordem do número:
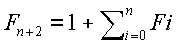 ,
, 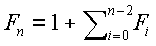
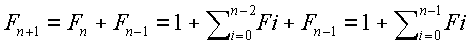
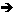
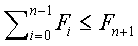
Anexo:
Algoritmo de Huffman
Huffman(C)
1 n := |C|
2 Q := C
3 for i:=1 to n-1 do
4 alocar um nó z
5 esquerda[z] := x := EXTRACT-MIN(Q)
6 direita[z] := y := EXTRACT-MIN(Q)
7 f[z] := f[x] + f[y]
8 INSERT(Q,z)
9 return EXTrACT-MIN(Q) // Retornar a raiz da árvore.