MO417 - Ata de exercícios

Heaps Binomiais e de Fibonacci

Resolução dos Exercícios do dia 25/04/2003
Última alteração: 12/05/2003
Redator: Nielsen Cassiano Simões

1. Proposta de resolução dos exercícios
1.1. Heaps Binomiais
1.2. Heaps de Fibonacci

1. Proposta de resolução dos exercícios

          Os exercícios propostos em aula tiveram uma de suas propostas de solução adicionadas nesta ata.

1.1. Heaps Binomiais

          19.1-1) Se x não é uma raiz de uma árvore binomial dentro de um heap binomial, de que modo grau[x] se compara a grau[p[x]]?
Resolução


grau[x] <= grau[p[x]]-1

Como x é filho de p[x], e p[x] é uma árvore binomial, então x também é uma árvore binomial, com grau no máximo igual ao grau de seu pai menos 1. Essa é uma das propriedades das árvores binomiais (4a. propriedade do Lema 19.1).
Lema 19.1 (Propriedades de árvores binomiais)
Para a árvore binomial B_k,
1. existem 2^k nós,
2. a altura da árvore é k,
3. existem exatamente Binômio(k, i) nós na profundidade i para i = 0,...,k, e
4. a raiz tem grau k, o qual é maior que o de qualquer outro nó; além disso, se os filhos da raiz são numerados da esquerda para a direita por k-1, k-2,...,0, o filho i é a raiz de uma subárvore B_i.


 

          19.2-3) Mostre o heap binomial que resulta quando o nó com chave 28 é eliminado do heap binomial mostrado na figura 19.8(c).





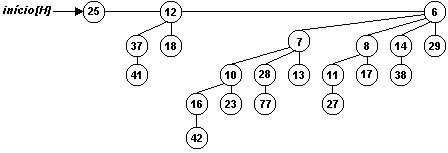
Figura 3: Figura 19.8(c) do livro texto.

Resolução


O resultado obtido foi:




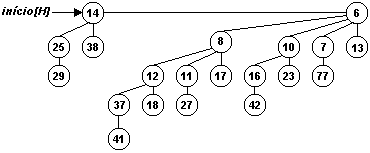
Figura 1: Heap Binomial resultante da solução do exercício 19.2-3.

Algoritmos

BINOMIAL-HEAP-DELETE(H,x)
 1 BINOMIAL-HEAP-DECREASE-KEY(H,x,-inf)
 2 BINOMIAL-HEAP-EXTRACT-MIN(H)

BINOMIAL-HEAP-DECREASE-KEY(H,x,-inf)
 1 if k > chave[x]
 2    then error "nova chave é maior que chave atual"
 3 chave[x] <- k
 4 y <- x
 5 z <- p[y]
 6 while z != NIL e chave[y] < chave[z]
 7     do trocar chave[y] <-> chave[z]
 8        |> Se y e z têm campos satélite, trocá-los também.
 9        y <- z
10        z <- p[y]

BINOMIAL-HEAP-EXTRACT-MIN(H)
 1 encontrar a raiz x com a chave mínima na lista de raízes de H
         e remover x da lista de raízes de H
 2 H' <- MAKE-BINOMIAL-HEAP()
 3 inverter a ordem da lista ligada de filhos de x
         e definir início[H'] de modo a apontar para o início da lista resultante
 4 H <- BINOMIAL-HEAP-UNION(H,H')
 5 return x

MAKE-BINOMIAL-HEAP()
 1 aloca e retorna um objeto H, onde início[H] = NIL.

BINOMIAL-HEAP-UNION(H1,H2)
 1 H <- MAKE-BINOMIAL-HEAP()
 2 início[H] <- BINOMIAL-HEAP-MERGE(H1, H2)
 3 libera os objetos H1 e H2 mas não as listas para as quais eles apontam
 4 if início[H] = NIL
 5    then return H
 6 anterior-x <- NIL
 7 x <- início[H]
 8 próximo-x <- irmão[x]
 9 while próximo-x != NIL
10    do if (grau[x] != grau[próximo-x]) or
            (irmão[próximo-x] != NIL e grau[irmão[próximo-x]] = grau[x])
11          then anterior-x <- x
12               x <- próximo-x
13          else if chave[x] <= chave[próximo[x]
14                  then irmão[x] <- irmão[próximo-x]
15                       BINOMIAL-LINK(próximo-x,x)
16                  else if anterior-x = NIL
17                       then início[H] <- próximo-x
18                       else irmão[anterior-x] <- próximo-x
19                       BINOMIAL-LINK(x, próximo-x)
20                       x <- próximo-x
21    próximo-x <- irmão[x]
22 return H

BINOMIAL-HEAP-MERGE(H1,H2)
 1 intercala as listas de raízes de H1 e H2 em uma única lista ligada que
          é ordenada por grau em ordem monotonicamente crescente.

BINOMIAL-LINK(y,z)
 1 p[y] <- z
 2 irmão[y] <- filho[z]
 3 filho[z] <- y
 4 grau[z] <- grau[z] + 1

  

1.2. Heaps de Fibonacci

          20.2-1) Mostre o heap de Fibonacci resultante da chamada a FIB-EXTRACT-MIN sobre o heap de Fibonacci mostrado na figura 20.3(m).




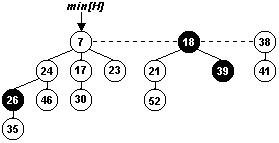
Figura 4: Figura 20.3(m) do livro texto.

Resolução


O resultado obtido foi:




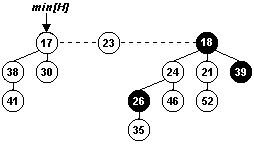
Figura 2: Heap de Fibonacci resultante da solução do exercício 20.2-1.

Algoritmos

FIB-HEAP-EXTRACT-MIN(H)
 1 z <- min[H]
 2 if z != NIL
 3    then for cada filho x de z
 4         do adicionar x à lista de raízes de H
 5            p[x] <- NIL
 6         remover z da lista de raízes de H
 7         if z = direito[z]
 8            then min[H] <- NIL
 9            else min[H] <- direito[z]
10               CONSOLIDATE(H)
11         n[H] <- n[H] - 1
12 return z

CONSOLIDATE(H)
 1 for i <- 0 to D(n[H])
 2   do A[i] <- NIL
 3 for cada nó w da lista de raízes de H
 4   do x <- w
 5      d <- grau[x]
 6      while A[d] != NIL
 7        do y <- A[d]
 8           if chave[x] > chave[y]
 9              then trocar x <-> y
10           FIB-HEAP-LINK(H,y,x)
11           A[d] <- NIL
12           d <- d + 1
13      A[d] <- x
14 min[H] <- NIL
15 for i <- 0 to D(n[H])
16   do if A[i] != NIL
17         then adicionar A[i] à lista de raízes de H
18              if min[H] = NIL or chave[A[i]] < chave[min[H]]
19                 then min[H] <- A[i]

FIB-HEAP-LINK(H,y,x)
 1 remover y da lista de raízes de H
 2 tornar y um filho de x, incrementando grau[x]
 3 marca[y] <- FALSE