Unicamp - Universidade Estadual de Campinas
IC - Instituto de Computação

MO417 - Algoritmos elementares de grafos 2 (Exercícios)

Aula dia: 16-Mai-2003
Última atualização: 19-Mai-2003
Redator: Fábio Batista Gomes - RA 022256

Proposta de solução dos exercícios:

22.3-2

Enunciado: Mostre como a 'busca em profundidade' funciona sobre o grafo da Figura 22.6. Suponha que o loop for das linhas 5 a 7 do procedimento DFS considere os vértices em ordem alfabética, e suponha que cada lista de adjacências esteja em ordem alfabética. Mostre os tempos de descoberta e término para cada vértice, e mostre também a classificação de cada aresta.

Solução: O algoritmo DFS começa executando pelo vértice q (ordem alfabética). O primeiro vértice adjacente a q é o vértice s. Recursivamente são visitados os vértices v, w. O próximo vértice adjacente a q é o vértice t. Recursivamente são visitados x, z e y, nesta ordem. Como a árvore não pode se estender mais por causa da orientação das arestas de y para r e u, o algoritmo inicia outra árvore com o próximo vértice não visitado (BRANCO). Então forma-se uma árvore a partir do vértice r. O único vértice adjacente a r que ainda não foi visitado é o vértice u. Segundo o algorítmo, a árvore gerada e a respectiva marcação do tempo de 'chegada' e 'saída' é a seguinte:

     
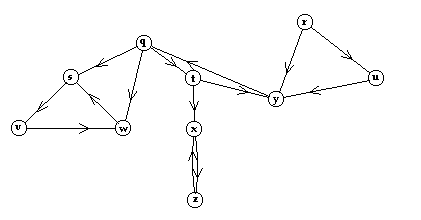
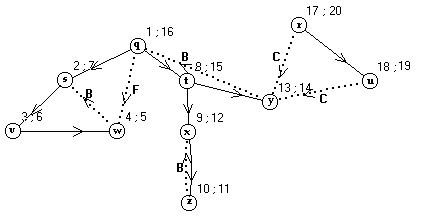
Figura 22.6                                                                                                                Solução

Algoritmo DFS

DFS(G)
1 for cada vértice u <- V[G]
2   do cor[u] <- BRANCO
3     PI[u] <- NIL
4 tempo <- 0
5 for cada vértice u pertencente a V[G]
6   do if cor[u] = BRANCO
7      then DFS-VISIT(u)

DFS-VISIT(u)
1 cor[u] <- CINZA
2 tempo <- tempo + 1
3 d[u] <- tempo
4 for cada v pertencente a Adj[u]
5   do if cor[v] = BRANCO
6      then PI[v] <- u
7        DFS-VISIT(v)
8 cor[u] <- PRETO
9 f[u] <- tempo <- tempo + 1

22.4-2

Enunciado: Forneça um algorítmo de tempo linear que tome como entrada um grafo acíclico orientado G = (V, E) e dois vértices s e t, e retorne o número de caminhos de s para t em G. Por exemplo, no grafo acíclico orientado da Figura 22.8, existem exatamente quatro caminhos do vértice p para o vértice v: pov, poryv, posryv e psryv. (Seu algoritmo só precisa contar os caminhos, não listá-los).

Solução: É apresentado o seguinte algoritmo como solução:

1 Ordenar topologicamente os vértices do grafo e colocá-los num vetor T
2 Associar o valor 0 a todos os vértices
3 Associar o valor 1 ao vértice s
4 for i <- pos[s] to pos[t] - 1
    do some o valor associado ao vértice T[i] ao valor associado
       de todo vértice acessível diretamente a partir de T[i]
5 return o valor associado ao vértice t


O passo 1 é O(V + E), o passo 2 é Theta(V), os passos 3 e 5 são Theta(1). No passo 4, no pior caso, todos os vértices e arestas são visitados, logo, é O(V + E). Portanto a complexidade total do algoritmo é O(V + E).

pos[v] = posição do vértice v no vetor T.

Alguns detalhes:
1. Feita a ordenação topológica em uma lista, o tempo gasto para passar para vetor é O(V);
2. O tempo gasto para se achar pos[v] no vetor T é O(V);
3. O algoritmo pode ser alterado de forma que o for do passo 4 percorra todo o vetor T. Desse modo, serão varridos todos vértices e arestas. Contudo, o passo 4 continua gastando tempo O(V + E) e o resultado será o mesmo.

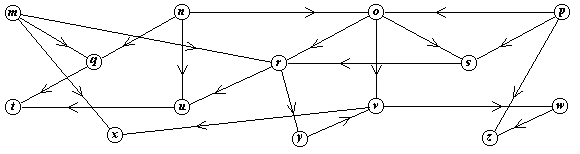
Figura 22.8

22.4-3

Enunciado: Forneça um algorítmo que determine se um dado grafo não orientado G = (V, E) contém um ciclo. Seu algoritmo deve ser executado no tempo O(V), independente de |E|.

Solução: Enquanto se executa o algorimo DFS, verifica-se a existência de arestas de retorno. Caso encontre pelo menos uma, significa a existência de ciclo. É apresentada a seguir uma modificação do algoritmo DFS.

Algoritmo DFS modificado para encontrar ciclos:

DFS(G)
1 ciclo <- false
2 for cada vértice u <- V[G]
3   do cor[u] <- BRANCO
4     PI[u] <- NIL
5 for cada vértice u pertencente a V[G]
6   do if cor[u] = BRANCO
7      then ciclo <- ciclo or DFS-VISIT(u)
8 return ciclo

DFS-VISIT(u)
1 cor[u] <- CINZA
2 for cada v pertencente a Adj[u]
3   do if cor[v] = CINZA
4     then return true
5   else if cor[v] = BRANCO
6     then PI[v] <- u
7       DFS-VISIT(v)
8 cor[u] <- PRETO
9 return false

Aresta de retorno é aquela que conecta um vértice u a um ancestral v em uma árvore produzida por busca em profundidade. Este tipo de aresta implica em um ciclo. A marcação de tempo não é necessária para esse problema, por isso foi desconsiderada.