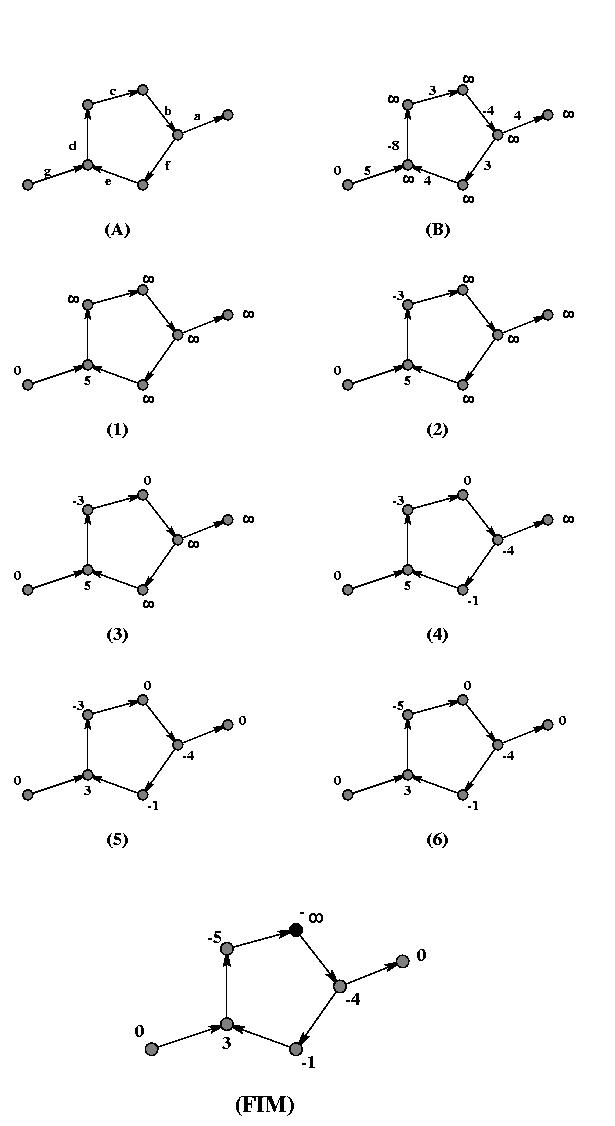
Figura 1: Contra exemplo para uma abordagem citada em aula.
MO417 – Complexidade de Algoritmos I
Caminhos Mais Curtos – Fonte Única 1
Ata de Exercícios: 23/05/2003
Redator: José Augusto Amgarten Quitzau
24.1-3 – Dado um grafo orientado ponderado G=(V,E) sem ciclos de peso negativo, seja m o máximo (sobre todos os pares de vértices u, v pertencentes a V) do número mínimo de arestas em um caminho mais curto de u a v. (Aqui, o caminho mais curto é por peso, não pelo número de arestas.) Sugira uma mudança simples no algoritmo de Bellman-Ford que permita encerrá-lo em m+1 passagens.
Solução:
1 INITIALIZE-SINGLE-SOURCE(G,s) 2 trocou <- true 3 while (trocou) 4 trocou <- false 5 for cada aresta (u,v) pertencente a E[G] 6 do trocou <- (trocou or RELAX-MODIFICADO(u,v,w))
RELAX-MODIFICADO(u,v,w) 1 if d[v] > d[u]+w(u,v) 2 then d[v] <- d[u]+w(u,v) 3 pai[v] <- u 4 return true 5 else return false
Comentário:
A função RELAX-MODIFICADO retorna um valor booleano que é verdadeiro somente quando o valor do vértice v é alterado. A variável trocou é inicializada com o valor false à cada iteração do loop das linhas 3 a 6. Assim que um vértice muda de valor, a expressão booleana na linha 6 força o valor da variável trocou a ser true e, a partir deste instante, ela não mais terá o valor false até uma nova execução da linha 4. Se nenhum valor é alterado, a variável trocou continua false após o loop das linhas 5 e 6, o que causa a terminação do loop das linhas 3 a 6.
24.1-4 – Modifique o algoritmo de Bellman-Ford de modo que ele defina d[v] como -infinito para todos os vértices v para os quais existe um ciclo de peso negativo em algum caminho a partir da origem até v.
Solução:
BELLMAN-FORD(G,w,s) 1 INITIALIZE-SINGLE-SOURCE(G,s) 2 for i <- 1 to |V[G]|-1 3 do for cada aresta (u,v) em E[G] 4 do RELAX(u,v,w) 5 for cada aresta (u,v) em E[G] 6 do if d[v] > d[u]+w(u,v) 7 then MARCA(v)
MARCA(v) 1 if d[v] != -infinito 2 then d[v] <- -infinito 3 for cada vértice z tal que existe (v,z) em E[G] 4 do MARCA(z)
Comentário:
Ao invés de parar e retornar "falso" quando encontra um vértice que poderia ser relaxado depois das |V|-1 passagens, esta versão marca o vértice v cujo valor de d[v] poderia ser diminuído e marca recursivamente todos os vértices acessíveis a partir dele de forma recursiva. Como sempre há um vértice a ser marcado no próprio ciclo de peso total negativo, todos os vértices acessíveis a partir dele são marcados, incluindo os do próprio ciclo.
Em aula, foi apresentada uma abordagem onde somente os vértices v que caem na condição da linha 6 são marcados. A Figura 1 apresenta um exemplo onde esta abordagem falha. A cada passagem, as arestas são relaxadas na ordem indicada pela Figura 1.A (ordem alfabética). A Figura 1.B mostra os pesos das arestas e o valores de d[v] após a execução do procedimento INITIALIZE-SINGLE-SOURCE. O algoritmo executa seis passagens de relaxamento das arestas, uma vez que o grafo tem sete vértices. A Figura 1.FIM mostra o único vértice que seria marcado por esta abordagem (em preto).
|
Figura 1: Contra exemplo para uma abordagem citada em aula. |
24-1 – Aperfeiçoamento de Yen para Bellman-Ford
Suponha que façamos a ordenação dos relaxamentos de arestas em cada passagem do algoritmo de Bellman-Ford como a seguir. Antes da primeira passagem, atribuímos uma ordem linear arbitrária v1, v2, ..., v|V| aos vértices do grafo de entrada G=(V,E). Em seguida, particionamos o conjunto de arestas E em Ef e Eb, onde Ef={(vi, vj) em E : i<j} e Eb={(vi, vj) em E : i>j}. (Suponha que G não contém nenhum autoloop, de forma que toda aresta está em Ef ou em Eb.) Defina Gf=(V,Ef) e Gb=(V,Eb).
Suponha que implementemos cada passagem do algortmo de Bellman-Ford da maneira descrita a seguir. Visitamos cada vértice na ordem v1, v2, ..., v|V|, relaxando as arestas de Ef que deixam o vértice. Depois, visitamos cada vértice na ordem v|V|, v|V|-1, ..., v1, relaxando as arestas de Ef que deixam o vértice.
Obs.: Deveríamos supor a. e b. corretas e responder apenas o item c.
Solução:
Não, pois a complexidade do algoritmo de Bellman-Ford implementado da maneira tradicional é O(VE) justamente porque todas as arestas são relaxadas Theta(V) vezes e teto(V/2) é Theta(V), logo, assintoticamente, o aperfeiçoamento não faz diferença.