UNICAMP - Universidade Estadual de Campinas

IC - Instituto de Computação

MO417 - Complexidade de Algorítmos I - 1º semestre/2003

prof. João Meidanis

Ata de aula

de 13 de junho 2003

Tema: Fluxo Máximo
Última alteração: 17/06/2003
 Redator: Éric Hainer Ostroski

26.3-1
            Execute o algorítmo de Ford-Fulkerson sobre o fluxo em rede da Figura 26.8(b) e mostre a rede residual após cada ampliação de fluxo. Numere os vértices em L de cima para baixo, desde 1 até 5, e em R de cima para baixo, desde 6 até 9. Para cada iteração, escolha o caminho em ampliação que seja lexicograficamente menor.

Rede de Fluxo a cada iteração:
 Descrição da iteração:
grafo inicial
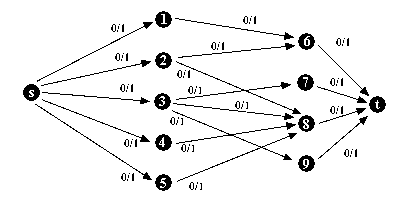
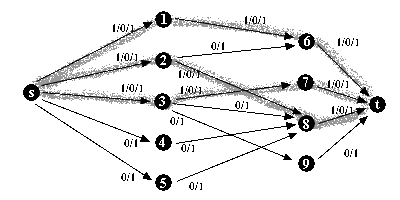
Este é o grafo inicial, como  na figura 26.8(b)

     Todos os caminhos tem de capacidade 1 (colocado à direita da barra), e é atribuído 0 para o fluxo (colocado à esquerda da barra) pois não existe caminho algum percorrido nesse momento.

     É gerada então a rede residual, indicando-se a capacidade restante em cada aresta, dada pela subtração do fluxo utilizado (zero para todos num primeiro momento) da capacidade inicial.
     Caminhos com peso nulo (0 - zero) de aresta não precisa ser representado.
     Os caminhos de retorno também devem ser gerados, indicando o fluxo que já foi utilizado. Eles são representados por uma aresta em direção oposta. (nesta etapa todas arestas de retorno são nulas, por isso não foram representadas)
     O menor caminho aumentante em ordem lexicográfica é indicado nesta rede.

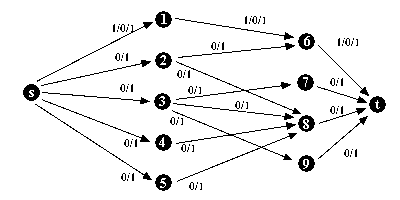
     O caminho aumentante escolhido tem o seu fluxo aumentado até a capacidade máxima possível, que é o menor valor de aresta encontrado no caminho da fonte s ao sumidouro t na rede residual.
     Continua-se considerando-se o valor mais a direita a capacidade da aresta e o valor mais a esquerda, o fluxo utilizado nessa aresta. Os valores intermediários ficam apenas como histórico das modificações feitas.

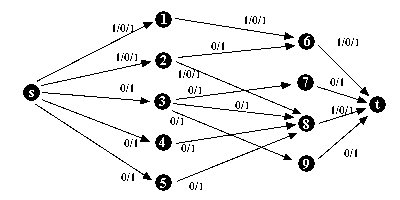
     Gera-se outra rede residual, indicando-se a capacidade restante em cada aresta, dada pela subtração do fluxo utilizado (zero para todos num primeiro momento) da capacidade inicial.
     Note que já existem arestas de retorno.
     O próximo caminho aumentante em ordem lexicográfica é indicado nesta rede.

     São atualizados os valores dos fluxos no grafo inicial, somando-se o caminho aumentante.

     Continua-se gerando redes residuais enquanto existir algum caminho da origem ao sumidouro.

     A rede de fluxo é atualizada com o caminho aumentante encontrado.

     É gerada ainda a rede residual, que nesse passo não possue qualquer caminho da origem ao sumidouro.
     Como não há caminho aumentante, conclui-se que o grafo obtido representa uma rede de fluxo máximo.

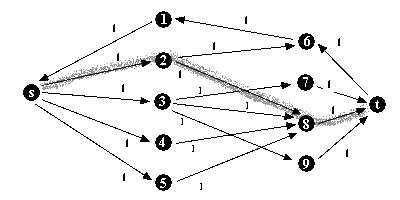
Destaque dos caminhos aumentantes que geraram a rede de fluxo máximo.

            Discutindo-se este exercício, foi proposta uma outra representação, esquemática em tabela sem usar figuras:
Dado o grafo inicial, como  na figura 26.8(b):

- Cria-se uma tabela com a primeira coluna indicando as arestas, a segunda coluna as respectivas capacidades e as próximas colunas contendo as alterações das capacidades.

Aresta Capacidade
inicial
 passo
1
 passo
2
 passo
3
s-1
1-s 		1
0 		0
1

s-2
2-s 		1
0
0
1
s-3
3-s 		1
0

0
1
s-4
4-s 		1
0


s-5
5-s 		1
0


1-6
6-1 		1
0 		0
1

2-6
6-2 		1
0


2-8
8-2 		1
0
0
1
3-7
7-3 		1
0

0
1
3-8
8-3 		1
0


3-9
9-3 		1
0


4-8
8-4 		1
0


5-8
8-5 		1
0


6-t
t-6 		1
0 		0
1

7-t
t-7 		1
0

0
1
8-t
t-8 		1
0
0
1
9-t
t-9 		1
0







26-4 Atualização do fluxo máximo
            Seja G = (V,E) um fluxo rede com origen s, depósito t e capacidades inteiras. Vamos supor que recebemos um fluxo máximo em G.

a. Suponha que a capacidade de uma aresta única  (u,v) ∈ E seja aumentada por 1. Forneça um algoritmo que rode em tempo O(V+E) para atualizar o fluxo máximo.

linha
 instrução
 explanação sobre a instrução
1.
 incrementar a capacidade de (u,v)
2.
 criar rede residual

3.
 rodar BFS na rede residual; se encontrar caminho aumentante, atualiza o fluxo; caso contrário, o fluxo inicial continua sendo máximo
 Caso o fluxo aumente, será por no máximo 1 unidade, portanto basta procurar caminho aumentante uma vez só, já que as capacidades são inteiras.


b. Suponha que a capacidade de uma aresta única  (u,v) ∈ E seja diminuída por 1. Forneça um algorítmo em tempo O(V+E) para atualizar o fluxo máximo.

linha
 instrução
 explanação sobre a instrução
1.
 Se aresta não é saturada:
 Aresta saturada é aquela onde fluxo = capacidade.
2.
      decrementar capacidade de (u,v)
3.
      retornar o fluxo original O fluxo continua válido e o corte mínimo não diminuiu
4.
 Senão
5.
      considerando apenas arestas com fluxo positivo, achar um caminho s-u e um caminho v-t
 constrói caminho de fluxo positivo s-t que contenha aresta (u,v). Tal caminho tem que existir pois passa fluxo positivo por (u,v).
6.
      decrementar fluxo dos caminhos s-u, u-v e u-t
 Fluxo fica uma unidade menor
7.
      decrementar capacidade (u,v) e criar rede residual
8.
      rodar BFS na rede residual; se encontrar caminho aumentante, atualiza o fluxo; caso contrário, o fluxo inicial continua sendo máximo
 Procura ver se a unidade de fluxo decrementada pode fluir por outro caminho.