Definições

Um genoma arbitrário formado por n genes será representado como uma permutação π = [π(1), π(2), …, π(n)] onde cada elemento de π representa um gene. O genoma identidade ι_n é definido como ι_n = [1, 2, …, n].

Uma transposição τ(x, y, z), onde 1 ≤ x < y < z ≤ n+1, é um evento de rearranjo que transforma π no genoma τπ = [π(1), …, π(x - 1), π(y), &hellip, π(z - 1), &pi(x), …, π(y - 1), π(z), …, π(n)].

Uma transposição de prefixo τ(1, x, y), onde 1 < x < y ≤ n+1, é um evento de rearranjo que transforma π no genoma τπ = [π(x), …, π(y - 1), π(1), &hellip, π(x - 1), &pi(y), …, π(n)].

Dados dois genomas π e σ, definimos a distância de transposição d(π, σ) entre estes dois genomas como sendo o menor número de transposições necessário para transformar π em σ, ou seja, o menor r tal que existam transposições τ₁, τ₂, …, τ_r com τ_r…τ₂τ₁π = σ. Chamamos distância de ordenação por transposições, d(π), a distância de transposição entre os genomas π e ι_n, ou seja, d(π) = d(π, ι_n).

Dados dois genomas π e σ, definimos a distância de transposição de prefixo d_p(π, σ) entre estes dois genomas como sendo o menor número de transposições de prefixo necessário para transformar π em σ, ou seja, o menor r tal que existam transposições de prefixo τ₁, τ₂, …, τ_r com τ_r…τ₂τ₁π = σ. Chamamos distância de ordenação por transposições de prefixo, d_p(π), a distância de transposição de prefixo entre os genomas π e ι_n, ou seja, d_p(π) = d_p(π, ι_n).

Um breakpoint para o problema de transposição de prefixos é uma posição i de uma permutação π tal que π(i)-π(i-1) ≠ 1, e 2 ≤ i ≤ n. Por definição, a posição 1 (início da permutação) é sempre considerada um breakpoint. A posição n+1 (fim da permutação) é considerada um breakpoint quando &pi(n) ≠ n. Denotamos por b_p(π) o número de breakpoints de um permutação.

Nota: O texto chama a atenção para o fato de a definição de breakpoint usada neste contexto diferir um pouco da usada normalmente na literatura, uma vez que aqui a posição 1 é sempre considerada um breakpoint.

Uma strip é uma subseqüência π(i..j) de π, i ≤ j, tal que i e j+1 são breakpoints e não há nenhum outro breakpoint entre estas posições.

Dada uma permutação π e uma transposição de prefixo τ, definimos Δb_p(π, τ) como a variação no número de breakpoints causada pela operação τ, isto é, &Deltab_p(π, τ) = b_p(τπ)-b_p(π).

Lemas e Teoremas Importantes

Para qualquer transposição τ(x, y, z) existem transposições de prefixo &tau₁(1, r, s) e &tau₂(1, t, u) tais que τ₂τ₁π = τπ.

Qualquer algoritmo de aproximação de fator k para o problema da distância de transposição pode ser transformado em um algoritmo de aproximação de fator 2k para o problema da distância de transposição de prefixo.

Dada a permutação π≠ι_n, onde n=|π|, sempre é possível obter uma transposição de prefixo τ tal que Δb_p(π, τ) ≤ -1.

Seja π uma permutação com b_p(&pi) = 3, então d_p(π) = 1.

Para toda permutação π diferente da identidade temos ⌈(b_p(π)-1)/2⌉ ≤ d_p(π) ≤ b_p(π)-2.

Qualquer algoritmo que produza transposições de prefixo de acordo com os Lemas 3.9 e 3.10 é um algoritmo de aproximção de fator 2 para o problema da distância de transposição de prefixo.

Seja π uma permutação arbitrária e d_p(π)=k sua distância de transposição de prefixo. Então existe uma seqüência ótima de transposições de prefixo τ₁, …, τ_k, tal que τ_k…τ₁π = ι_n, onde n = |π|, e Δb_p(τ_i-1…τ₁π, τ_i) ≤ 0 para cada 1 ≤ i ≤ k.

Discussões em Sala de Aula

Apresentação de dois algoritmos de aproximação para o problema da distância de transposição de prefixo. Um com fator de aproximação 3 e outro com fator de aproximação 2.

Existem problemas de otimização que se sabe que são NP-Difíceis, o que significa que ninguém conhece um algoritmo que resolva o problema em tempo polinomial. No entanto, em alguns casos é possível determinar um algoritmo polinomial cujo maior desvio possível da solução ótima pode ser determinado. Imaginemos um problema de minimização de um valor X associado à cada resposta possível. Se conseguirmos provar que um algoritmo polinomial fornece uma resposta para a qual o valor associado não ultrapasse 1,5 vezes o valor mínimo para X, então temos na verdade uma 1,5-aproximação para o problema, ou seja, um algoritmo cujo fator de aproximação é 1,5. No caso de problemas de minimização, normalmente se prova que o algoritmo é uma k-aproximação para o problema determinando-se um limite inferior i para o valor minimizado e um limite superior s para o valor da resposta encontrada pelo algoritmo, desta forma podemos determinar k=s/i.

O algoritmo de aproximação de fator 3 se baseia no fato de já existir um algoritmo de aproximação de fator 3/2 para o problema da distância de transposição. Pelo Lema 3.3, este algoritmo pode ser transformado em um algoritmo de aproximação de fator 3 para a distância de transposição de prefixo.

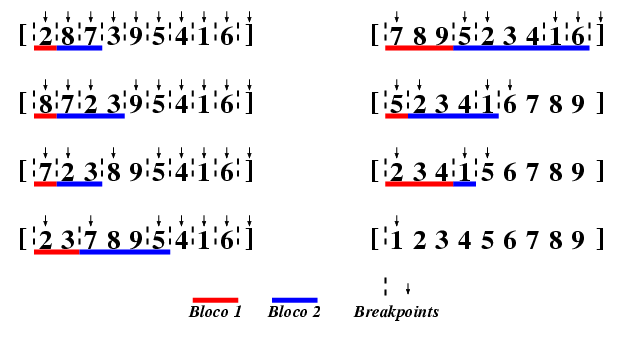
O algoritmo de aproximação de fator 3 se baseia no Teorema 3.13, pois ele utiliza a transposição de prefixo da prova do Lema 3.9 para criar uma série de transposições de prefixo de acordo com os Lemas 3.9 e 3.10.

A transposição de prefixo τ da prova do Lema 3.9 é a seguinte: Sejam π&neι_n uma permutação, onde n=|π|, e k o último elemento da primeira strip de π. Se k<n, τ=τ(1, π^-1(k)+1, π^-1(k+1)). Se k=n, τ=τ(1, π^-1(k)+1, n+1). A Figura 1 exemplifica uma série de transposições que ordena π=[2 8 7 3 9 5 4 1 6].

Figura 1: Exemplo de ordenação por transposições de prefixo da permutação π=[2 8 7 3 9 5 4 1 6]. O primeiro bloco da transposição é destacado por um traço vermelho, enquanto o segundo bloco da transposição por prefixo é marcado com um traço azul. Breakpoints são marcados de duas maneiras: setas marcam a posição do breakpoint, tal como na definição, enquanto linhas tracejadas marcam os pontos de quebra do genoma.