Solução:
Podemos reformular a pergunda da seguinte maneira, para tentarmos entender melhor: O artigo da Anne Bergeron afirma que escolhendo qualquer uma das reversões de escore máximo (garantidamente seguras) a distância obtida vai ser a mesma na execução do algoritmo completo. Contudo, o Algoritmo 1 citado na questão termina em uma permutação totalmente positiva. Será que essa permutação será a mesma seja qual for a reversão maximal que escolhermos? [1]
Temos, então, dois casos para analisar. Se a aplicação do Algoritmo 1 for suficiente para ordenar a permutação, é fácil ver que a permutação positiva retornada é igual para qualquer escolha que fizermos entre as reversões de score maximal. A dificuldade está em provar esse resultado se houverem permutações totalmente positivas não ordenadas durante o caminho da busca. [2]
Um modo interessante de resolver esse impasse seria obter uma permutação que alcançasse resultados diferentes dependendo das opções do caminho de ordenação. Mas, infelizmente, parece que obter um exemplo de uma permutação que no caminho de ordenação encontre mais de uma reversão de score máximal em algum passo, e que leve o algoritmo 1 a resultados diferentes quando escolhemos reversões distintas, é difícil. [3]
Uma outra forma de solucionar o problema seria obter uma prova matemática formal. Contudo, optamos por não entrar no mérito de uma prova como essa, pois, provas como essa são longas e demandam muito tempo que poderia ser usado para a apresentação de outros tópicos interessantes e essa apresentação de tópicos variados sobre bio-informática são mais pertinentes a esse curso. [4]
Foi levantada, então, a hipótese de que não faria diferença para o resultado final do Algoritmo 1, baseada na intuição dos colegas e apoiada em alguns resultados de outros papers estudados ou citados em aulas anteriores. Mesmo assim os colegas não conseguiam enxergar uma solução satisfatória por esse caminho. [5]
Também o professor não tinha uma resposta formada, mas sua intuição que dizia que "[...] no final do Algoritmo 1 parece que chegaremos ao mesmo lugar, pois escolhendo sempre uma das reversões maximais estaremos mexendo só em componentes boas, de uma forma segura [...]". [6]
Concluímos que, para solucionar o problema proposto, "[...] devemos ver apenas o essencial: quando você mexe nas componentes boas, você não mexe em partes de componentes ruins, podendo apenas reverter totalmente uma ou mais componentes ruins. Devemos notar que o algoritmo 1 termina deixando "strips" na parte que ordena da permutação, que corresponde às componentes boas. Então, a parte ruim que sobra parece ser a mesma para quaisquer escolhas que tenhamos lançado mão no caminho de ordenação da permutação original. Afinal, quando mexe na boa, mexe somente naquela boa. As ruins podem ser viradas e reviradas várias vezes, mas acabarão numa mesma orientação, pois ao terminar o Algoritmo 1 temos todos os elementos positivos." E essa passou a ser a nossa resposta oficial. [7]
Tendo marcado como resolvido esse problema, entramos no mérito de outros algoritmos que não o Algoritmo 1 proposto nesse exercício. Foi comentado que talvez fazer apenas reversões de score máximo não dê o mesmo resultado que se utilizássemos todas as reversões seguras possíveis. [8]
Esse ponto foi anotado, e tentamos encaixá-lo em um suposto algoritmo que arruma todas as componentes ruins antes de iniciar uma fase parecida com o Algoritmo 1 a fim de terminar a ordenação, obtendo distância mínima. Talvez nesse caso a ordem das transformações faça diferença. Essa sentença foi ressaltada depois de tentarmos um 'hurdle merging' (indicado com o pontilhado vermelho) entre os hurdles H e H' na Figura 1. Note que cada linha cheia dentro do ciclo da Figura 1 representa uma componente ruim. [9]
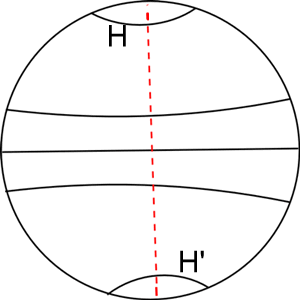
Figura 1: Um Hurdle Merging
As contribuições para essa Ata vieram nas seguintes oportunidades (principalmente):
1 [Prof. Meidanis, reformulando o enunciado]
2 [Colega Douglas, explicando o resultado do grupo de estudos]
3 [Colega Mário, falando sobre os resulados parciais obtidos pelo grupo de estudo]
4 [Prof. Meidanis, considerando a dificuldade da prova formal de algum resultado para essa solução]
5 [Mário, falando sobre resultados de outros papers de algoritmos que arrumavam os obstáculos ou antes de tudo, ou durante o caminho de ordenação]
6 [Prof. Meidanis, considerando sobre esse ponto da discussão, a intui ção parece ser a melhor escolha para continuar.]
7 [Prof. Meidanis, retomando a direção da discussão, apresentando resultados de uma forma mais clara]
8 [Colega Peterson, levantando a questão dos resultados de outros papers novamente. ela já tinha sido ressaltada por Mário]
9 [Prof. Meidanis, falando sobre os algoritmos que arrumam obstáculos antes de tudo e desenhando no quadro]
A ata foi redigida pelo aluno Peterson Katagiri Zilli.