Ache todas as uniões de componentes conexos e todas as classes de gêmeos da seguinte instância: U=abcdefghijklmno, C={abdijmn, adimn, an, bcj, cefghklo, efghklo, efho, fgkl, mn}.
SOLUÇÃO: O grafo de sobreposição estrita das restrições em C é o seguinte:
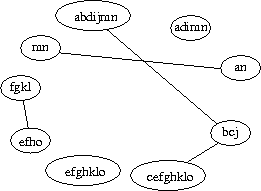
Há cinco componentes conexas. Duas delas (adimn e efghklo) são formadas por um único conjunto, portanto nestes casos a união é o próprio conjunto. Um destes conjuntos é igual à união de uma outra conpomente (efho-fgkl), de modo que há somente quatro uniões distintas. São elas:
- abcdefghijklmno
- adimn
- efghklo
- amn
As classes de gêmeos podem ser encontradas aplicando-se o algoritmo de determinação da partição mais grossa que refina as restrições dadas, com o seguinte resultado:
- a
- bj
- c
- di
- eho
- f
- gkl
- m
- n
Construa a árvore PQR correspondente à entrada acima pelo algoritmo offline discutido em aula.
SOLUÇÃO: A seguir vemos uma possível escolha de conjuntos H1, H2, H3, etc. para decompor recursivamente o problema, até chegar em instâncias primas, as quais resultam em nós P, Q ou R:

Juntando todos os pedaços, o resultado final é o seguinte:

Dos conjuntos elencados no ex.1, quais correspondem efetivamente a nós da árvore PQR?
SOLUÇÃO: Todos, exceto di. Este resultado corrobora a teoria, que diz que todas as uniões de componentes serão nós, mas nem todas as classes de gêmeos serão nós.