Write in algebraic form as a product of disjoint permutation cycles the reversal involving blocks B and C of the linear chromosome below.
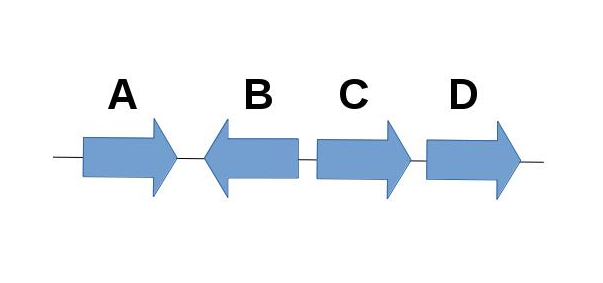
Write in algebraic form as a product of disjoint permutation cycles the excision of the segment involving blocks A, B, and C of the linear chromosome below, forming a circular intermediate.

Find the algebraic distance between the two genomes below.

Find a sorting rearrangement with weight 1 or less taking π to σ of the previous exercise, according to the algebraic concept of distance.
Iterate the previous exercise as many times as needed to find an optimal series of light algebraic sorting operations leading from π to σ. 'Light' operation here means an operation with weight 1 or less.