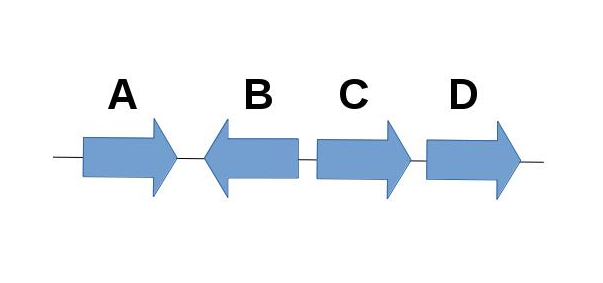
1. Write in algebraic form as a product of disjoint permutation cycles the reversal involving blocks B and C of the linear chromosome below.
Exercises marked with (*) require further reading/search beyond the suggested texts.
1. Write in algebraic form as a product of disjoint permutation cycles the reversal involving blocks B and C of the linear chromosome below.

Answer:
From the image above, we write π in adajcency algebraic form:
π = (-A -B) (B C) (-C D)
We wish to reverse blocks B and C by multiplying π by an operation ρ, so we need:
ρπ = (-A -C) (B C) (-B D)
We now discover ρ by solving:
(A -C) (B C) (-B D) = ρ (-A -B) (B C) (-C D)
If we multiply a given genome π, in algebraic form, by its inverse, we obtain the identity. Therefore, the equation x = y (A B) is equivalent to x (A B) = y. Applying this reasoning several times in the equation above, we get:
(-A -C) (B C) (-B D) = ρ (-A -B) (B C) (-C D)
(-A -C) (B C) (-B D) (-C D) = ρ (-A -B) (B C)
(-A -C) (B C) (-B D) (-C D) (B C) = ρ (-A -B)
(-A -C) (B C) (-B D) (-C D) (B C) (-A -B) = ρ
Lastly, we simplify ρ so that it becomes a product of disjoint cycles:
ρ = (A) (-A D) (B) (-B -C) (C) (D -A) (-D)
Which is the same as:
ρ = (-A D) (-B -C)
© 2015 Joao Meidanis