Consider the computational graph below. Suppose the inputs are x = 1 and w = 2, the intermediate node computes the product, and f is a ReLU activation function.

Apply forward and backpropagation passes along the graph for these values of input. For each pass, fill in the corresponding table below, with the order in which the nodes are visited, and the values computed.

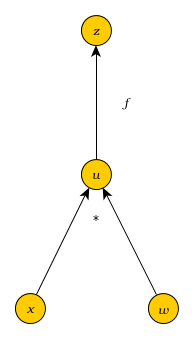
Forward Pass
Order	Node	Value
1	A.: x	A.: 1
2	A.: w	A.: 2
3	A.: u	A.: x*y = 2
4	A.: z	A.: max(0,u) = 2

Backpropagation Pass
Order	Node	Value
1	A.: z	A.: \(\frac{\partial z}{\partial z}\) = 1
2	A.: u	A.: \(\frac{\partial z}{\partial u}\)(u) = 1
3	A.: x	A.: \(\frac{\partial z}{\partial x}\) = \(\frac{\partial z}{\partial u}\frac{\partial u}{\partial x}\) = 1*w = 2
4	A.: w	A.: \(\frac{\partial z}{\partial w}\) = \(\frac{\partial z}{\partial u}\frac{\partial u}{\partial w}\) = 1*x = 1