DESENVOLVIMENTO E AVALIAÇÃO DE UM SISTEMA PARA ANÁLISE CINEMÁTICA TRIDIMENSIONAL DE MOVIMENTOS HUMANOS
R. M. L. Barros, R. Brenzikofer, N. J. Leite e P. J. Figueroa
RESUMO -- Esta pesquisa consiste da concepção e avaliação de um sistema para análise cinemática tridimensional de movimentos humanos, baseado em registros estereoscópicos de vídeo. O conceito orientador do sistema é discutido e o ambiente computacional desenvolvido é apresentado. O problema do rastreamento (tracking) de movimentos humanos em seqüências de imagens digitais é formulado, usando conceitos de processamento de imagens, em particular morfologia matemática. O método implementado para reconstrução de coordenadas espaciais a partir de projeções é testado. Os resultados obtidos com o sistema foram exemplificados na análise de marcha de dois sujeitos. As características principais do sistema proposto são a independência em relação a equipamentos dedicados, a possibilidade de utilizar marcadores passivos e ativos sob condições experimentais diversas, a confiabilidade dos resultados, a simplicidade de operação e o baixo custo.
Palavras-chave: Biomecânica, Morfologia Matemática, Reconstrução Tridimensional.
INTRODUÇÃO
A análise de movimentos humanos em seqüências de imagens digitais tem despertado grande interesse em diferentes áreas do conhecimento. Cada vez mais faz-se necessário e torna-se possível que o movimento humano seja estudado em detalhes, de maneira sistemática e como objeto de investigação científica. A análise biomecânica do movimento humano permite avaliações da performance humana no esporte, no trabalho ou nas atividades da vida diária como andar, correr, entre outras. Em particular, sistemas para análise cinemática tridimensional de movimentos humanos têm sido utilizados como instrumento de diagnóstico em processos recuperatórios de pessoas com distúrbios, deficiências, anomalias ou limitações com reflexos sobre o aparelho locomotor.
Em conseqüência dos benefícios potenciais desta análise, diferentes sistemas têm sido desenvolvidos recentemente com tal finalidade: Woltring (1989), Berme e Capozzo (1991), Boenick e Näder (1990). Os sistemas capazes de realizar a análise cinemática tridimensional de movimentos humanos diferem nos graus de automatização de seus procedimentos, nas restrições que impõem à situação experimental e na sofisticação e custos dos equipamentos que utilizam.
A principal diferença entre equipamentos para registro dos movimentos é a utilização de câmeras de infravermelho ou de vídeo. Nos sistemas onde câmeras de infravermelho são utilizadas, marcadores ativos (LEDs), atados ao corpo do sujeito, emitem luz infravermelha registrada pelas câmeras. Uma variação deste tipo de sistema adota marcadores passivos que refletem a luz vinda de emissores infravermelho. Estes sistemas têm a vantagem de operar com maior resolução espacial e temporal nos registros, além do que a identificação automática (por software) dos marcadores é facilitada, uma vez que esses marcadores destacam-se fortemente dos demais objetos presentes nas imagens. Em contrapartida, os sistemas que utilizam marcadores ativos obrigam o sujeito investigado a deslocar-se transportando algum tipo de fonte, além dos cabos que conectam os diversos LEDs. Nos sistemas que utilizam marcadores passivos infravermelho, as principais limitações dizem respeito as restrições ao ambiente de filmagem e aos tipos de movimentos que podem ser estudados. Em ambos os casos, os custos são elevados devido ao uso de câmeras especiais.
A utilização de câmeras de vídeo permite maior flexibilidade na seleção dos movimentos a serem estudados, diminui as restrições ao ambiente de coleta e permite a maior difusão deste tipo de análise, uma vez que os custos são menores. Exceção feita a movimentos muito rápidos, a freqüência de aquisição das câmeras de vídeo (60 Hz) fornece uma resolução temporal suficiente para grande número de análises em biomecânica. Contudo, a medição automática das projeções dos pontos de interesse nas seqüências de imagens é dificultada pela complexidade das imagens, dado o menor contraste entre os marcadores e os demais objetos na cena.
O sistema proposto consiste fundamentalmente de equipamentos não dedicados e um programa de computador. Os equipamentos necessários para o funcionamento do sistema são: a) câmeras de vídeo, b) conversor analógico-digital para sinal de vídeo (Capture Board), preferencialmente capaz de adquirir o sinal de vídeo em tempo real (60 Fields/s), c) computador PC 486 ou superior, monitor capaz de operar com paletas de mais de 256 cores simultâneas, mínimo de 8 Mbytes de memória RAM e sistema operacional windows for 32bits (Windows 95 ou NT) e d) tripés para as câmeras de vídeo.
O sistema permite o uso de câmeras de vídeo, entre outras, e integra recursos de detecção automática de marcadores (tracking) baseados em conceitos de processamento de imagens, em particular morfologia matemática. Além disso, algoritmos para calibração das câmeras e reconstrução tridimensional de coordenadas foram desenvolvidos e implementados. Desta forma, diferentemente dos demais sistemas disponíveis, o sistema desenvolvido não necessita de equipamentos dedicados e permite que diferentes tipos de marcadores sejam usados. Em casos específicos, é possível até que características próprias do objeto de interesse possam ser utilizadas como padrão a ser identificado nas seqüências de imagens.
Apresentamos, portanto, o conceito norteador do sistema desenvolvido pelo Laboratório de Instrumentação para Biomecânica - Faculdade de Educação Física e pelo Instituto de Computação - UNICAMP, os principais recursos implementados e os resultados obtidos pelo sistema em aplicações selecionadas. O programa dedicado ao sistema foi denominado "Dvideow", Digital Video for Biomechanics for Windows 32 bits.
RECONSTRUÇÃO DE COORDENADAS
A fim de descrevermos o movimento de uma partícula é necessário que conheçamos sua posição no espaço, em relação a um dado referencial, em função do tempo. A posição da partícula no espaço, relativa ao referencial, é definida com a ajuda de três coordenadas independentes, por exemplo, as coordenadas cartesianas. Em relação ao parâmetro tempo (t), temos:
![]() (1)
(1)
A obtenção de coordenadas espaciais de pontos a partir do registro estereoscópico de suas projeções em imagens é uma metodologia bastante difundida na Biomecânica, denominada reconstrução tridimensional de coordenadas. Os procedimentos de calibração de câmeras e reconstrução tridimensional que utilizamos foram inicialmente propostos por Abdel-Aziz e Karara (1971) e são conhecidos como DLT (Direct Linear Transformation). As equações básicas do método de reconstrução tridimensional de coordenadas (DLT) são mostradas a seguir.
 (2)
(2)
Este sistema de equações (2) é aplicado duas vezes, a primeira para quantificar os parâmetros da transformação (calibração) e a segunda para efetuar a reconstrução propriamente dita. Para a calibração das câmeras temos que: xi e yi são as coordenadas de tela do i-ésimo ponto de um sistema de referências conhecido, para cada câmera k; Xi, Yi e Zi são as coordenadas espaciais do i-ésimo ponto de referência e nkh (h=1,...,11) são os 11 parâmetros da transformação para a k-ésima câmera, a serem determinados. O número mínimo de pontos de referência com coordenadas conhecidas é seis.
Para a reconstrução tridimensional temos que: xki e yki são as coordenadas de tela do ponto de interesse na i-ésima imagem, da k-ésima câmera. nkh (h=1,...,11) são os 11 parâmetros de calibração para a k-ésima câmera e Xi, Yi e Zi são as coordenadas espaciais do ponto de interesse na i-ésima imagem, a serem determinadas. O número mínimo de câmeras a serem usadas é dois.
Tanto no caso da calibração de cada câmera como na reconstrução de coordenadas, o sistema de equações apresentado é sempre superdimensionado, conseqüentemente mais de uma solução para o problema. Efetuamos então, uma otimização por quadrados mínimos das soluções possíveis.
Para os casos em que a sincronização eletrônica das câmeras de vídeo não é possível, incorporamos ao sistema um conjunto de procedimentos que permitem a sincronização dos registros, por software. Estes procedimentos consistem em: a) determinar os parâmetros de sincronização das câmeras, defasagem inicial em tempo e diferença na freqüência de aquisição, e b) corrigir os efeitos da defasagem temporal por meio de interpolação numérica das projeções da trajetória, em cada câmera. A determinação dos parâmetros de sincronização pode ser feita pela adição de um sinal simultâneo aos registros das câmeras ou por meio de métodos de otimização. Uma descrição detalhada da solução do problema pode ser encontrada em Barros (1997).
TRACKING DOS MARCADORES
A obtenção automática das coordenadas de tela dos pontos de interesse (tracking) nas seqüências de imagens baseou-se no tratamento genérico do problema do processamento de imagens, conceitualizado originalmente na área de ciências da computação, associado a conhecimentos das características de movimentos humanos, estes estudados pela biomecânica. A fundamentação teórica para a estruturação dos algoritmos de detecção dos marcadores foi a morfologia matemática. A seguir, apresentaremos algumas de suas operações básicas consideradas neste trabalho.
Morfologia Matemática
A morfologia matemática (Serra, 1992; Haralick et alli, 1987), inicialmente definida para imagens binárias e logo estendida para imagens em níveis de cinza, contém ferramentas para processamento de imagens baseadas em geometria e forma. As operações morfológicas simplificam as imagens, mantendo as principais características dos seus objetos.
Seja f uma imagem binária e discreta, { f(x) Î 0,1: x Î Z2 }, onde Z denota o conjunto de números inteiros. Esta imagem pode ser representada por um conjunto X definido como X={x Î Z2: f(x)=1}. Uma transformação morfológica f é dada pela relação da imagem (conjunto de pontos X) com outro conjunto de pontos B, denominado elemento estruturante.
O complemento Xc de um conjunto é definido como Xc={x Î Z2 : f(x)=0}. A família de um elemento estruturante B é a seqüência de elementos estruturantes obtida ao girar-se o elemento estruturante B de um ângulo dado (por exemplo, 45 ou 90 graus). Um elemento estruturante composto Bc é denotado por um par de conjuntos disjuntos, Bc = (B1,B2), em que B1 ={x Î Z2 : f(x)=1} e B2={x Î Z2 : f(x)=0}.
Dilatação e Erosão -- As duas operações básicas da morfologia matemática são a dilatação e a erosão. A dilatação de uma imagem binária X com um elemento estruturante B é dada por:
![]() (3)
(3)
A erosão de uma imagem binária X com um elemento estruturante B é definida como:
![]() (4)
(4)
As duas operações acima podem ser estendidas para uma imagem numérica (em nível de cinza) f. Para um elemento estruturante planar (de representação binária) a dilatação e erosão podem ser definidas por:
![]() (5)
(5)
![]() (6)
(6)
Abertura e Fechamento -- Aplicando-se iterativamente a dilatação e a erosão, é possível eliminar alguns detalhes específicos da imagem, menores do que o elemento estruturante, sem destruir a geometria global das partes não suprimidas. A abertura, por exemplo, suaviza os contornos, quebra picos agudos e elimina pequenas ilhas. Esta operação é definida por:
![]() (7)
(7)
Por sua vez, o fechamento fecha aberturas agudas e golfos longos e finos, elimina pequenos buracos e espaços entre contornos. Esta operação é dada por:
![]() (8)
(8)
Afinamento e Espessamento -- Estas operações morfológicas utilizam um elemento estruturante composto Bc. A função g(x) correspondente ao afinamento da imagem f por Bc é dada por:
![]() (9)
(9)
Analogamente, o espessamento de f por Bc, originando a imagem g(x) é definido por:
 (10)
(10)
Linha Divisora de Águas (LDA) -- Aplicando-se o afinamento com uma família homotópica de elementos estruturantes B, definimos as linhas divisoras de águas da função imagem. Estas linhas representam as zonas de influência dos mínimos regionais. Uma definição intuitiva de LDA (Vicent e Soille, 1993) pode ser dada considerando o grafo da imagem f como uma superfície topográfica. Ao se inundar esta superfície, as linhas definidas para impedir a junção das águas provenientes das bacias constituem as LDA da superfície.
Segmentação de marcadores
A fase de segmentação, no processamento de imagens, visa a extração de características dos marcadores, os quais podem ser adesivos colados ou marcas desenhadas sobre a pele do sujeito. Utilizamos principalmente a marca branca rodeado de cor preta (veja figura 1) para facilitar a extração. Neste caso da extração da marca, consideramos a extração do contorno da marca, para esta finalidade selecionamos, dentre os recursos implementados, algumas ferramentas da morfologia matemática, conforme definidas anteriormente.
Para melhor compreensão da adequação dos conceitos de morfologia matemática ao problema, mostramos, na figura 1, a seqüência de procedimentos de segmentação utilizada para a extração de um marcador, bem como descrevemos os objetivos em cada etapa. O processamento da imagem é feito por regiões. As regiões são definidas como lugar onde temos a máxima probabilidade de encontrar o marcador e é determinada no processo de predição.
Entre os contornos selecionados a escolha será feita no processo de casamento de padrões (matching). A segmentação no processo de tracking melhora a seleção e diminui o número de possíveis matchings falsos que podem ocorrer durante a comparação da marca com o modelo.
Predição do centro de região de busca
A predição é o recurso utilizado para determinar o centro das regiões de busca, onde a marca pode ser encontrada com maior probabilidade e onde a segmentação será aplicada. Esta informação é baseada nos valores determinados nos quadros anteriores. Os principais objetivos da predição são a redução do custo computacional em segmentar e procurar matchings em toda a imagem e a facilitação do processo de classificação dos marcadores. Um dos métodos utilizados para esta finalidade é a filtragem Kalman (Kalman, 1960).
O filtro de Kalman é uma técnica recursiva de atualização usada para determinar os parâmetros corretos de um modelo de processo. Dados alguns valores iniciais, pode-se predizer e ajustar os parâmetros do modelo através de cada nova medição, obtendo a estimativa do erro em cada atualização. A sua habilidade para incorporar os efeitos de erros e sua estrutura computacional fizeram com que o filtro de Kalman tivesse um amplo campo de aplicações, especialmente no que se refere à análise de trajetórias em visão computacional (Cox e Hingorani, 1996; Rohr, 1994).
Os elementos que constituem o filtro de Kalman para esta aplicação são definidos da seguinte forma: ![]() é o vetor que contém os parâmetros no tempo
é o vetor que contém os parâmetros no tempo ![]() , ou seja
, ou seja ![]() , onde x e y denotam as coordenadas da posição do marcador e
, onde x e y denotam as coordenadas da posição do marcador e ![]() são a representação das velocidades nas direções respectivas.
são a representação das velocidades nas direções respectivas.




I II III IV



V VI VII

VIII
Figura 1. Seqüência de procedimentos para a segmentação e o resultado da medição automática.
I. A região do joelho do sujeito na imagem é convertida em níveis de cinza
II. Espessamento da marca, com o objetivo de dilatar a marca branca e melhorar a região do contorno.
III. Fechamento, com o intuito de eliminar as pequenas ilhas geradas pelo espessamento, para que a marca mantenha a forma circular.
IV. Gradiente da imagem, utilizado para extrair os contornos, o gradiente consiste em realizar a dilatação menos a erosão.
V. Afinamento, com o objetivo de melhorar a definição dos contornos.
VI. LDA, a linha divisora de águas elimina os contornos abertos e etiqueta as regiões.
VII. Seleção dos contornos baseado em seus perímetros (possíveis marcadores).
VII. Uma das imagens da seqüência com os resultados da medição automática sobrepostos.
Matching
Determinar a similaridade entre dois padrões (Matching) não é tarefa fácil, devido a fatores que influenciam a qualidade da imagem, por exemplo, a mudança de intensidade da luz ao longo da seqüência, a mudança na forma dos objetos, a presença de ruídos, etc. O critério de casamento pode ser definido de diferentes formas. A correlação entre padrões é um critério geral (Sonka, 1993). Aplicamos a correlação entre a matriz correspondente a marca, definida inicialmente pelo operador na primeira imagem, e todas as matrizes, de tamanho 2K+1 por 2L+1, existentes na região de busca, de acordo com a seguinte expressão:
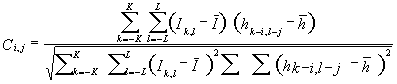 (11)
(11)
Onde ![]() e
e ![]() são as médias da imagem I e do marcador h respectivamente.
são as médias da imagem I e do marcador h respectivamente.
Para achar o melhor casamento é calculado o máximo valor das correlações.
![]() (12)
(12)
Onde R é a região de busca.
As coordenadas (i, j) para as quais l é máximo são consideradas como o centro do marcador. Para definir a matriz h pode ser utilizada a última marca encontrada, ou a primeira marca definida, dependendo da variação da forma e cor dos marcadores ao longo da seqüência.
A primeira opção é utilizada se a intensidade e a forma do marcador mudam bastante quadro a quadro. Isto permite atualizar a marca e considerar as variações nas imagens. A desvantagem desta opção é a possibilidade de perder a marca num quadro e continuar procurando a marca falsa. Esta desvantagem pode ser eliminada se utilizarmos a segunda alternativa, especialmente para os casos de oclusão das marcas. Um dos problemas com esta opção está relacionado com a baixa correlação, à medida que a intensidade da imagem muda, complicando assim, a escolha correta do marcador.
O critério utilizado para a escolha do marcador é o valor máximo de l
, mas este nem sempre garante um bom resultado , já que em certas circunstâncias podem aparecer valores de ![]() bastante próximos. Por este motivo, devem ser utilizados outros critérios de decisão além de casamento de padrões, por exemplo a distância ao ponto predito. Neste caso, pode ser criada uma lista ordenada de possíveis casamentos acima de um certo valor de correlação.
bastante próximos. Por este motivo, devem ser utilizados outros critérios de decisão além de casamento de padrões, por exemplo a distância ao ponto predito. Neste caso, pode ser criada uma lista ordenada de possíveis casamentos acima de um certo valor de correlação.
As regiões geradas durante o processo de LDA na segmentação foram etiquetas, dando um valor fixo para o fundo, assim, o casamento de padrões é aplicado apenas para os pontos (i, j) onde o valor é diferente do que o fundo. Para cada região de etiqueta diferente do fundo é calculada a máxima correlação, criando assim uma lista de tamanho igual ao numero de regiões. Finalmente, a fila é ordenada.
RESULTADOS
Avaliação dos algoritmos de calibração e reconstrução
Para que pudéssemos avaliar a variabilidade das medidas obtidas da reconstrução tridimensional de coordenadas, realizada a partir do sistema proposto, projetamos um experimento para a análise dos resultados coletados. O experimento seguiu a sugestão feita por Morris e Macleod (1990) na avaliação de erros de medidas em sistemas de análise baseados em vídeo.
O experimento consistiu em utilizar o sistema na reconstrução das trajetórias espaciais de três pontos marcados sobre um corpo rígido em movimento. Este objeto foi colocado em suspensão por um único ponto de sustentação realizando um movimento pendular. O ângulo inicial a partir do qual o corpo rígido foi abandonado e começou a oscilar foi de aproximadamente quinze graus.

Figura 2. Representação esquemática da montagem experimental para avaliação da variabilidade das medidas obtidas da reconstrução tridimensional de coordenadas.
Conforme representado na figura 2, duas câmeras Hi-8 com freqüência de captura 50 Hz (sistema PAL) foram utilizadas para registrar o movimento pendular de um objeto rígido que continha três pontos marcados sobre o mesmo. O procedimento de calibração das câmeras foi realizado e o tempo de aquisição do movimento do objeto foi de 3.22 segundos.
As distâncias entre os pontos foram medidas cinco vezes cada uma diretamente no objeto, tendo-se encontrado os seguintes valores: distância do ponto 1 ao ponto 2 (1-2) 200 ± 1 mm; a distância do ponto 1 ao 3 (1-3) 400 ± 1 mm; e distância do ponto 2 ao 3 (2-3) 200 ± 1 mm. Estes valores foram tomados como valores esperados.
As duas seqüências de imagens foram digitalizadas e medidas permitindo assim a reconstrução 3D dos pontos e o cálculo das distâncias. Os resultados estão resumidos na tabela (1) e na figura (3).
Tabela 1. Valores obtidos para a distância média e o desvio-padrão entre os pontos marcados sobre o objeto rígido, obtidos no sistema Dvideow, para 161 quadros (3.22 segundos de aquisição).
|
Média (mm) |
Desvio-padrão (mm) |
Repetições |
|
|
Variação da distância 1-2 |
201.2 |
0,8 |
161 |
|
Variação da distância 1-3 |
402.6 |
1,0 |
161 |
|
Variação da distância 2-3 |
201.1 |
0,9 |
161 |
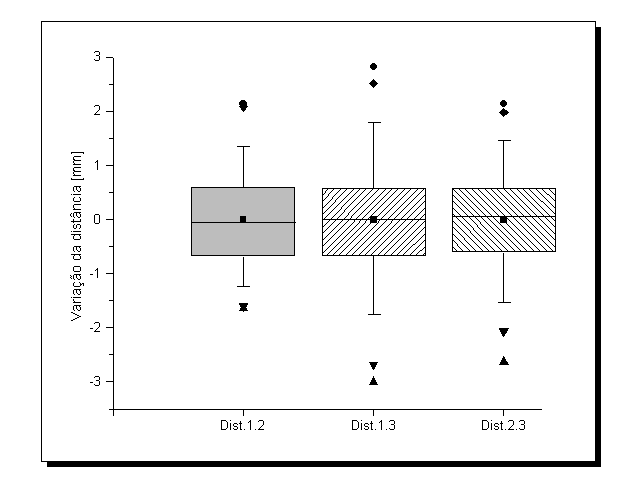
Figura 3. Boxplot da variação em relação à média da distância entre os pontos 1-2, 1-3 e 2-3 marcados sobre o objeto rígido.
As distâncias obtidas pelo sistema Dvideow apresentam flutuações aleatórias normais com desvio-padrão da ordem de 1 mm. Esses erros são pequenos quando considerada a escala da imagem. Neste experimento, por exemplo, o enquadramento vertical, cerca de 1.5 m, foi tal que cada linha de vídeo ou pixel na tela corresponde a uma altura de 4 mm, consideramos aceitável as diferenças de menos de 1 % observadas entre as distâncias medidas e os valores esperados.
Exemplo de aplicação do sistema na determinação do ângulo do joelho durante a marcha
Para exemplificar e ilustrar o uso do sistema Dvideow, apresentamos uma comparação das características da marcha de dois sujeitos, observando, em particular, a angulação do joelho em função do tempo. É importante lembrar que objetivo do exemplo é apresentar os resultados metodológicos obtidos e não uma avaliação dos possíveis problemas clínicos dos sujeitos. Para isso, selecionamos uma situação em que um sujeito com uma alteração de marcha clinicamente evidenciada é comparado a um sujeito normal. Note-se que apenas o comportamento de uma variável será estudada, a angulação do joelho, não caracterizando portanto uma análise completa de marcha.
Os sujeitos comparados foram: um sujeito adulto (24), altura 1.75 m, massa 75 kg, sem qualquer histórico de problemas no aparelho locomotor, que passaremos a denominar sujeito normal ou representado por (KL). Um sujeito adulto (24), altura 1.73 m, massa 60 kg, com histórico de intervenção cirúrgica no joelho esquerdo, decorrente de acidente automobilístico, que implantou um pino de fixação na patela, que denominaremos sujeito operado e será representado por (JO). O sujeito (JO) realizou sessões de fisioterapia durante três meses após a cirurgia. Os dados foram coletados um ano após o término do tratamento. Ainda era possível perceber qualitativamente uma ligeira alteração na marcha.
Com o objetivo de observar as diferenças, comparamos a variável ângulo do joelho na marcha de ambos com o sistema Dvideow. Em cada sujeito foram feitas marcações com lápis especial para pintura sobre a pele, onde demarcaram-se três pontos de interesse, de maneira a permitir a posterior determinação de trajetórias e ângulos articulares. Os três pontos indicados procuraram estimar externamente a posição do trocanter maior, do eixo de rotação do joelho e do maléolo lateral, no membro direito e esquerdo de cada sujeito.
Cada sujeito caminhou por três vezes com o lado direito voltado para as câmeras e repetiu mais três passagens com o lado esquerdo. A freqüência de registro das câmeras foi de 25 Hz e o tempo de aquisição foi correspondente a um ciclo de passada. O ciclo da passada foi tomado como o intervalo entre o primeiro contato com o solo de um calcanhar até o novo contato do mesmo calcanhar. A partir das coordenadas espaciais desses três pontos marcados, o ângulo do joelho foi determinado (J). A extração dos marcadores foi feita automaticamente, utilizando-se os procedimentos exemplificados na extração de marca na figura 1.
A figura 4 mostra os resultados filtrados dos valores dos ângulos do joelho direito do sujeito normal (KLD), joelho esquerdo do sujeito normal (KLE), joelho direito do sujeito operado (JOD) e joelho esquerdo do sujeito operado (JOE), depois de realizados os procedimentos de normalização.
Observando-se as diferenças nas curvas de angulação do joelho direito e esquerdo de cada sujeito, percebe-se que os resultados obtidos pelo sistema permitem identificar diferenças importantes. Comparando-se lado dirente e esquerdo de cada sujeito, nota-se a maior simetria na marcha do sujeito normal, como esperado. Além disso, pode-se identificar em que fase do ciclo da passada as diferenças são mais acentuadas, neste caso, isso ocorre para o sujeito operado na fase do ciclo correspondente ao apoio no solo.

Figura 4: Curvas médias do ângulos do joelho direito e esquerdo do sujeito operado e normal.
DISCUSSÃO E CONCLUSÃO
A idéia central do trabalho, sintetizada no conceito do sistema, mostrou-se abrangente e viável. A abrangência pode ser percebida pela diversidade de problemas e aplicações da análise cinemática dentro da biomecânica, e mesmo fora dela, que o sistema permite estudar. Ao estruturar-se o sistema de maneira a liberá-lo de equipamentos dedicados, um único ambiente para coleta de dados, ou de um determinado tipo de marcador fez-se mais do que favorecer a difusão do sistema. Possibilitou-se a aplicação da análise cinemática tridimensional em contextos nos quais esta análise não seria possível.
Em particular no que se refere ao tracking automático de padrões, os resultados obtidos são extremamente satisfatórios. A construção de um ambiente computacional que integra inúmeros recursos de extração de padrões em imagens digitais, fortemente fundamentados teoricamente, indica que o sistema poderá ser aplicado em diferentes contextos com grande sucesso.
Como o sistema concentra seus recursos no ambiente computacional, a sua aplicação em um novo contexto ou aplicação torna-se, principalmente, um problema de formulação e implementação do algoritmo correto. Problemas aparentemente distintos têm sido tratados com sucesso a partir do mesmo ambiente computacional, como por exemplo: análise de marcha; análise de movimentos do tórax durante a respiração ou mesmo trajetórias de bolas de vôlei sacadas durante uma partida. Assim, o sistema proposto mostrou-se adequado para, dentro de sua especificidade, ser aplicado em diferentes áreas do estudo da Biomecânica.
AGRADECIMENTOS
Ao Serviço Alemão de Intercâmbio Acadêmico (DAAD), Fundação de Amparo à Pesquisa do Estado de São Paulo (FAPESP), Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq ) e Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (CAPES) pelo apoio financeiro a realização desta pesquisa.
REFERÊNCIAS
ABDEL-AZIZ, Y. I., KARARA, H. M. (1971). "Direct linear transformation from comparator coordinates into object-space coordinates". Proc. ASP/UI Symp. on Close-Range Photogrammetry. Urbana, Illinois.
BARROS, R. M. L. (1997) "Concepção e implementação de um sistema para análise cinemática de movimentos humanos". Tese de Doutorado, Faculdade de Educação Física, Universidade Estadual de Campinas, Campinas, Brasil.
BERME, N., CAPPOZZO, A. (1990) "Biomechanics of Human Movement: Application in Rehabilitation, Sport and Ergonomics". Bertec Corporation. U.S.A.
BOENICK, U., NÄDER, M. (1991) "Gangbildanalyse. Stand der Mebtechnik und Bedeutung für die Orthopädie-Technik". Internationales Symposium Gangbildanalyse. Mecke Druck und Verlag, Berlin.
COX, I. J., Hingorani, S. L. (1996) "An efficient implementation of reid’s multiple hypotesis tracking algorithm and its evaluation for purpose of visual tracking". ". IEEE Trans Pattern Analysis and Machine Intelligence, 18(2), p. 138-150, 2.
HARALICK, R. M., STERNBERG, S. R., ZHUANG, X., (1987) "Image analysis using mathematical morphology". IEEE Trans Pattern Analysis and Machine Intelligence, 9(4):, p. 532-549, 7.
KALMAN, R. E. (1960) "A new approach to linear filtering and prediction problems". ASME J. Basic. Eng., p. 35-45, 3.
MORRIS, J. R. W., MACLEOD, A. (1990) "An Investigation of the Source and Characteristics of Noise in a Video-Based Kinematic Measurement System". In: Models, Connection with Experimental Apparatus and Relevant DSP Techniques for Functional Movement analysis, Deliverable F, CAMARC (A1012) CEC/AIM Project. June.
ROHR, K. (1994) "Towards Model-Based Recognition of Human Movements in Image Sequences". CVGIP: Image Understandings, 59(1), p. 94-115.
SERRA, J. (1992) "Image Analysis and Mathematical Morfology". Academic Press, London.
SONKA, M., HLAVAC, V., BOYLE, R.(1993) "Image Processing. Analysis and Machine Vision". Chapman & Hall Computing.
VICENT, L., SOILLE, P. (1991) "Wathershed in digital spaces: Na efficient algorithm based on immersion simulations". IEEE Trans Pattern Analysis and Machine Intelligence, 13(6):, p. 583-598, 6.
WOLTRING, H. J. (1989) "One Hundred Years of Photogrammetry in Biolocomotion". In Proceeding of the Symposium on Biolocomotion: A Century of Reserch Using Moving Picture, Formia, Italy.
DEVELOPMENT AND EVALUATION OF A SYSTEM FOR THREE-DIMENSIONAL KINEMATIC ANALYSIS OF HUMAN MOVEMENTS
R. M. L. Barros, R. Brenzikofer, N. J. Leite e P. J. Figueroa
ABSTRACT--This research consists of the conception and evaluation of a system for three-dimensional kinematic analysis of human movements, based on stereoscopic video registers. The guiding concept of the system is discussed and the developed computational environment presented. The problem of the human movement tracking in sequences of digital image is formulated using concepts of image processing, in particular mathematical morphology. The implemented method for reconstruction of space co-ordinates from projections is evaluated. The results obtained with the system were exemplified in gait analysis of two subjects. The main features of the proposed system are the independence in relation to dedicated hardware, the possibility to use passive and active markers under distinct experimental condition, the goodness of the results, the simplicity to operate and the low cost.
Keywords: Biomechanics, Mathematical Morphology, Three-dimensional Reconstruction.