Até agora, quando queríamos guardar muitos dados na memória, usávamos vetores. Só que vetores têm limite, ou seja, temos que definir de antemão o número máximo de elementos que um vetor pode ter. O que acontece se não tivermos esse limite? Ou seja, o que fazemos se esse limite não for definido? Uma alternativa seria criar um vetor imenso, gastando um mundo de memória. Mas ainda assim correríamos o risco de estourar o limite do vetor. Então, o que fazer?

A solução ideal seria se pudéssemos, à medida que recebemos algum dado, separar um espaço na memória para ele e armazená-lo lá. Ou seja, nosso limite seria dado pela quantidade de memória disponível no computador.

Naturalmente, como separamos um espaço na memória e guardamos um valor lá, temos que, de algum modo, saber qual é esse pedaço de memória, ou seja, precisamos de uma espécie de endereço que nos leve a esse pedaço para que, futuramente, possamos acessar o que guardamos lá ou mesmo guardar algo lá.

Então como fazemos isso em Pascal? Com ponteiros. Ponteiros nada mais são do que variáveis que guardarm o endereço de uma região de memória, podendo essa região conter a informação que quisermos.

Vejamos como declaramos ponteiros em Pascal:

  VAR nome_do_ponteiro : ^tipo_apontado;
	

Nesse caso, tipo_apontado é qualquer tipo, simples ou definido pelo usuário, do Pascal. Ou seja, não posso fazer:

  VAR ptr : ^ARRAY[1..10] OF integer;
	

mas posso fazer:

  TYPE vetor = ARRAY[1..10] OF integer;
  VAR ptr : ^vetor;
	

Agora vamos ver como usar um ponteiro. Suponha a declaração:

  VAR ptr : ^integer;
	

O que temos aqui? Apenas uma variável, chamada ptr, que é um ponteiro para um inteiro, ou seja, ela guarda um endereço de memória onde pode ser armazenado um inteiro. Mas de qual pedaço ela tem o endereço? Nenhum. Para efetivamente dar um valor a ptr temos que fazer:

  new(ptr);
	

A forma geral do new é

  New(variável_de_ponteiro);
	

O que, então, isso faz? Esse comando simplesmente diz ao sistema operacional para que este separe um pedaço de memória em que caiba um inteiro (o tipo apontado por ptr), guardando o endereço deste pedaço em ptr. E qual é esse endereço? Não sabemos, e nem precisamos saber, pois o Pascal abstrai tudo isso. Ou seja, podemos agora usar a variável ptr quase como se fosse um integer comum. Por que quase? Veja abaixo:

  VAR ptr : ^integer;

  BEGIN
    new(ptr); {separei um pedaço de memória para um inteiro}

    ptr^ := 2; {coloquei o valor 2 nesse pedaço de memória}

    ptr^ := ptr^ * 3; {faço esse pedaço de memoria receber o triplo
                       do que lá havia}
  END.
	

Viu como fizemos? "ptr^" pode ser usada como qualquer variável integer. Veja agora o programa abaixo:

  VAR p1 : ^integer;
      p2 : ^integer;

  BEGIN
    new(p1); {reservei um pedaço de memória para um inteiro,
              fazendo p1 apontar para ele}

    p2 := p1; {fiz p2 apontar para o mesmo pedaço de memória
               que p1 aponta}

    p1^ := 4; {coloquei o valor 4 nesse pedaço de memória}

    writeln(p2^); {escrevi o valor que está no pedaço de
                   memória apontado por p2, ou seja, 4, pois
		   p2 aponta para o mesmo pedaço de memória
		   que p1}

    p2^ := p2^ + 3; {adicionei 3 ao valor que havia no pedaço
                     de memória apontado por p2 e armazenei
		     novamente nesse pedaço o resultado}

    writeln(p1^); {escrevo o conteúdo da memória apontada por
                   p1, ou seja, 7, pois p1 aponta para o mesmo
		   pedaço de memória que p2 aponta}
  END.
	

Como isso funciona? Vejamos por partes:

• Quando fizemos new(p1), separamos (ou, como dizemos, alocamos) espaço na memória suficiente para um inteiro, guardando o endereço desse espaço em p1, ou seja, fizemos p1 apontar para lá:
  
• Ao fazer p2 := p1 (note que não é p2^ := p1^), guardamos uma cópia do endereço que estava em p1 em p2. Ou seja, fazemos p2 apontar para a mesma região de memória que p1 apontava:
• Ao fazermos p1^ := 4 guardamos 4 nessa região:
• Ao lermos p2^ no write, simplesmente lemos o valor que está na região da memória apontada por p2, ou seja, 4.
• Ao fazermos p2^ := p2^ + 3, pegamos o conteúdo da região de memória apontada por p2, somamos 3 a este e armazenamos o resultado de volta nessa mesma região:
• Ao lermos p1^ no write, novamente lemos o valor que está na região de memória apontada por p1, ou seja, 7, já que esta é a mesma região que é apontada por p2 e que foi modificada no passo anterior.

  p2^ := p1^;
	

estamos copiando o conteúdo da região de memória apontada por p1 para a região de memória apontada por p2. Já se fizermos

  p2 := p1;
	

estaremos fazendo p2 apontar para a mesma região de memória apontada por p1.

Agora que sabemos como carregar valores com ponteiros, como fazemos para "zerar" um ponteiro? Ou seja, para dizer que ele não aponta para lugar nenhum?

  p1 := NIL;
	

Se não fizermos isso, ele conterá um endereço de memória que pode já ter sido liberada pelo programa, ou que pode não pertencer ao programa, o que geraria um erro quando da execução.

E, por falar em liberar memória, como fazemos se quisermos liberar a memória que reservamos com new?

  Dispose(variável_de_ponteiro);
	

ou seja

  Dispose(p1);
	

Dispose avisa ao sistema operacional que não vamos mais precisar desse pedaço de memória, liberando esta. SEMPRE libere a memória que não vai mais usar para não esgotar os recursos da máquina.

Cuidado com o seguinte erro:

  VAR p1 : ^integer;
      p2 : ^integer;

  BEGIN
    new(p1);

    p2 := p1;

    p1^ := 4;

    Dispose(p2);

    writeln(p1^)
  END.
	

isso pode gerar um erro, pois já liberei a memória apontada por p2, que é a mesma apontada por p1

Vale também lembrar que, ao final do programa, se você não liberou a memória usada, o computador a libera para você. Ainda assim é uma boa prática limpar seu lixo.

E se agora quisermos um ponteiro para um tipo mais complexo, como registro?

  TYPE reg = RECORD
               cp1 : real;
	       cp2 : integer;
	       cp3 : ARRAY[1..10] of char
	     END;

  VAR p : ^reg;

  BEGIN
    New(p);
  END.
	

Pronto! Aloquei espaço para o meu registro. Ou seja, na memória foi reservado espaço suficiente para guardar os 3 campos do nosso registro. E como acessamos ou mudamos o valor desses campos?

  TYPE reg = RECORD
               cp1 : real;
	       cp2 : integer;
	       cp3 : ARRAY[1..10] of char
	     END;

  VAR p : ^reg;
      i : integer;

  BEGIN
    new(p);

    p^.cp1 := 3.12;
    p^.cp2 := Round(p^.cp1); {guardei 3}

    FOR i:=1 TO 10 DO
      p^.cp3[i] := Chr(Ord('a') + i);

    writeln(p^.cpq,' - ', p^.cp2,' - ',p^.cp3[5]);

    Dispose(p)
  END.
	

Ou seja, agimos como se "p^" fosse o nome do registro. E se em vez de registro quisermos lidar com um vetor?

  TYPE vet = ARRAY[1..10] of integer;

  VAR p : ^vet;

  BEGIN
    new(p);

    p^[1] := 4;
    p^[2] := 5;
    p^[3] := p^[1] + p^[2];

    writeln(p^[1],' + ',p^[2],' = ',p^[3]);

    Dispose(p)
  END.
	

Novamente, agimos como se "p^" fosse o nome do vetor.

Com ponteiros, as operações permitidas são = e <>. Assim ,não posso fazer +, - etc. Ou seja, as únicas operações que posso usar com ponteiros são:

  p1 = p2   ->  True se ambos apontam para a mesma região de memória
  p1 <> p2  ->  True se ambos apontam para regiões diferentes
	

Agora que já vimos o que são ponteiros, vamos aprender, na próxima seção, a usá-los.

Suponha que queremos ler uma lista de dados. Até aí tudo bem. Agora suponha que não conhecemos o número total de dados. Como fazemos então?

Seria desejável seguir o seguinte algoritmo:

  inicialmente a lista está vazia
  enquanto o usuário não manda parar de ler
    leio um dado
    coloco este dado na lista
	

assim fica fácil não? Mas como fazer isso em Pascal? Usando ponteiros. Como? Com uma lista ligada. O que, então, é uma lsita ligada?

Uma lista ligada é uma lista onde cada elemento - chamado de nó - contém um valor e um ponteiro para o elemento seguinte. Assim, sabendo onde está o primeiro elemento da lista, podemos chegar a qualquer outro elemento. Há vários tipos de listas ligadas:

• Simples:
  
  O sinal de aterramento significa que este ponteiro é NIL, ou seja, não aponta para lugar nenhum.
• Circular:
  
  
• Duplamente ligada:
  
  

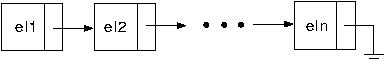
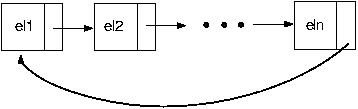
Mas e qual as vantagens e desvantagens de cada uma? Listas duplamente ligadas são fáceis de se percorrer, mas ocupam mais espaço na memória. Note que nessas eu posso, a partir de um elemento, voltar na lista, percorrê-la de trás para frente, pois tenho ponteiros que medizem onde estão o próximo elemento e o anterior.

As circulares simples são fáceis de percorrer e não ocupam muita memória. Mas se o número de elementos for grande, vai se comportar quase como uma lista simples.

Qual lista é a melhor? Depende do problema a ser resolvido.,p> Agora vamos definir operações básicas em listas:

• Criação de uma lista
• Inclusão de um elemento na lista
• Exclusão de um elemento da lista
• Esvaziamento da lista
• Contagem do número de elementos da lista
• Inclusão de um elemento na posição i
• Exclusão do iº elemento na lista
• Busca da posição do primeiro elemento de valor x
• Exclusão do primeiro elemento de valor x
• etc

Antes de mais nada, vamos definir nossa lista:

  TYPE tipo = real;
       p_no = ^no;
       no   = RECORD
                valor : tipo;
		prox  : p_no
              END;
	

Agora vamos definir o procedimento de criação da lista.

  PROCEDURE Cria(VAR cabeca : p_no);
  BEGIN
    cabeca := NIL
  END;
	

Pronto! O que fizemos com isso? Dissemos que a lista está vazia ao darmos um valor "nada" à cabeça desta. Se não fizermos isso, a cabeça pode conter lixo indesejável.

Agora vamos incluir um elemento na lista. A questão é: onde? Você decide. Pode ser no início, pode ser no meio (caso você queira ordenar a lista enquanto a constrói) e pode ser no fim. Nesse caso, vamos por no fim. Então, como faremos?

Suponha que temos a seguinte lista:

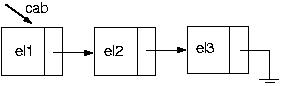
Vamos, então, colocar um elemento em seu final

• Alocamos o espaço para o novo elemento, fazendo q apontar para ele, e o abastecemos com valor
  
• Usamos um ponteiro auxiliar, p, para apontar para a cabeça da lista
  
• Precorremos a lista com p até que este aponte para o último elemento
  
• Fazemos o próximo elemento de p (que agora aponta para o fim da lista) ser q, ou seja, fazemos q ser o novo fim da lista
  

• Alocamos o espaço para o novo elemento e o abastecemos com valor
  
• Fazemos a cabeça da lista ser esse novo elemento

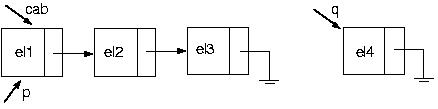
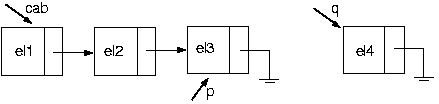
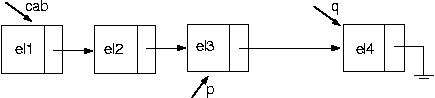
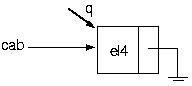
  PROCEDURE Inclui(VAR cabeca : p_no; elemento : tipo);
  VAR q : p_no; {o novo elemento}
      p : p_no; {auxiliar}
  BEGIN
    {aloco espaço para o novo elemento}
    New(q);

    {abasteço os valores nesse}
    q^.valor := elemento;
    q^.prox := NIL;

    {vejo onde coloco q na lista}
    IF cabeca <> NIL THEN
    BEGIN
      {a lista não estava vazia}
      p := cabeca;

      {vou até o fim da lista}
      WHILE p^.prox <> NIL DO p := p^.prox;

      {agora p é o último elemento, pois p^.prox = NIL}

      {faço o próximo elemento de p ser q, ou seja, q é o novo fim}
      p^.prox := q
    END
    ELSE {a lista está vazia. Faço q ser a cabeça}
      cabeca := q
  END;
	

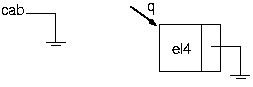
Vamos agora excluir um elemento da lista. Novamente, qual? Você escolhe! Vamos tomar como política a exclusão do primeiro elemento da lista. Como faremos isso?

Suponha a lista:

Vamos, então, retirar um elemento de seu início:

• Primeiro fazemos p apontar para o início da lista:
  
• Depois fazemos a cabeça apontar para o segundo elemento:
  
• Eliminamos agora o elemento apontado por p

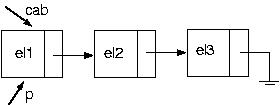
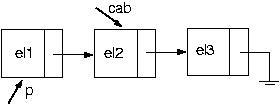
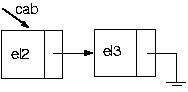
  PROCEDURE Exclui(VAR cabeca : p_no; VAR valor:tipo);
  VAR p : p_no; {auxiliar}
  BEGIN
    IF cabeca <> NIL THEN
    BEGIN
      {a lista não está vazia}
      p := cabeca;

      {faço a cabeça apontar para o próximo}
      cabeca := cabeca^.prox;

      {retorno o valor que está em p}
      valor := p^.valor;

      {mato o elemento apontado por p}
      Dispose(p);
    END
    {else a lista está vazia, não há o que tirar}
  END;
	

Suponha que queremos simplesmente matar a lista inteira, como fazemos isso? Da mesma forma que excluímos um elemento, só que não devolvemos valor algum:

• Coloco um ponteiro p na cabeça da lista
• Enquanto p não for nil
  • Faço a cabeça apontar para o próximo de p
  • Mato p
  • Faço p apontar para a cabeça

  PROCEDURE Limpa(VAR cabeca : p_no);
  VAR p : p_no; {auxiliar}
  BEGIN
    p := cabeca;

    WHILE p <> NIL DO
    BEGIN
      cab := p^.prox;
      Dispose(p);
      p := cab
    END
  END;
	

E como fazemos para contar os elementos de uma lista? Basta criar um contador e percorrer a lista incrementando o contador:

• Coloco um ponteiro p na cabeça da lista e zero o contador cont
• Enquanto p não for nil
  • Incremento cont
  • Faço p apontar para o próximo elemento

  FUNCTION NumEl(cabeca : p_no) : integer;
  VAR p : p_no; {auxiliar}
  BEGIN
    p := cabeca;
    NumEl := 0;

    WHILE p <> NIL DO
    BEGIN
      p := p^.prox;
      NumEl := NumEl + 1
    END
  END;
	

Agora, usando algumas das funções acima, vamos incluir um novo nó na posição i da nossa lista. Como faremos isso? Suponha a seguinte lista

• Primeiro fazemos p apontar para o início da lista:
  
• Em seguida movemos p até o elemento anterior à posição em que queremos incluir (suponha que queremos incluir na 3ª posição):
  
• Criamos, então, espaço para o novo elemento, fazendo q apontar para ele:
  
• Fazemos, então, o próximo elemento de q ser o próximo de p:
  
• E o próximo elemento de p ser q:
  

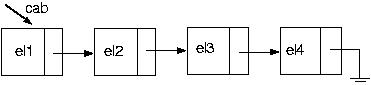
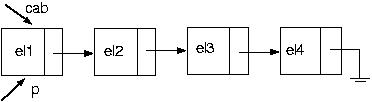
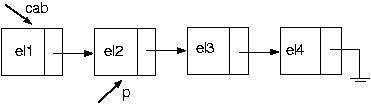
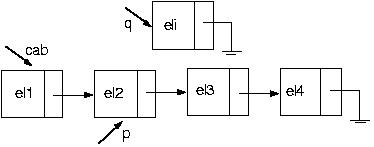
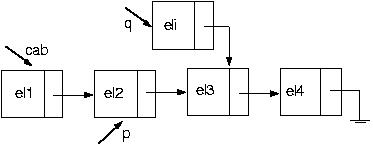
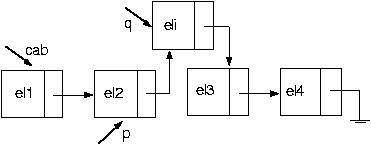
E se quisermos incluir na última posição? Funciona? Claro! Pois pararei com p no último elemento.

E se a lista estiver vazia? Nesse caso, basta criar o elemento e fazer a cabeça apontar para ele (veja abaixo como incluir na primeira posição). Note que nesse caso, o único i aceitável é 1.

E se a posição pedida for 1? Esse é um caso um pouco mais complicado, pois não há como parar um elemento antes, o que indica que nosso algoritmo falha. Como fazer, então?

• Primeiro criamos espaço para o novo elemento, fazendo q apontar para ele:
  
• Fazemos, então, o próximo elemento de q ser a cabeça:
  
• E a cabeça apontar para q:
  

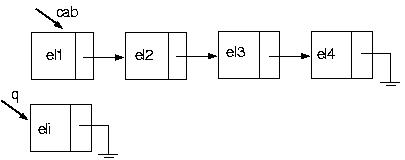
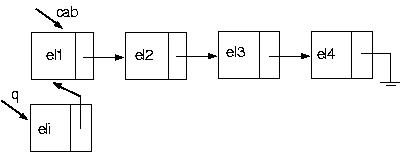
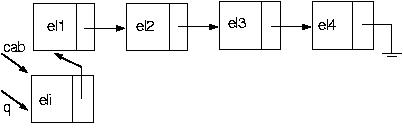
  PROCEDURE IncluiEmPos(VAR cabeca:p_no;valor:tipo;posicao:integer);
  VAR p : p_no;    {auxiliar}
      q : p_no;    {o novo elemento}
      i : integer; {contador do FOR}
  BEGIN
    {testo se a posição é válida}
    IF (posicao <= (NumEl(cabeca) + 1)) AND (posicao > 0) THEN
    BEGIN
      {é uma posição válida. O +1 é porque se tem 5 elementos
       posso por na posição 6, por exemplo (embora não na 7)}

      {crio o novo elemento}
      new(q);
      q^.valor := valor;
      q^.prox := NIL;

      IF posicao=1 THEN {quero na primeira posição}
      BEGIN
        {se a lista estiver vazia, não há problema aqui}

	{faço o próximo de q ser a cabeça}
	q^.prox := cabeca;

	{faço a cabeça ser q}
	cabeca := q
      END
      ELSE BEGIN {é outra posição}
        {note que aqui a lista jamais estará vazia, senão
	 NumEl retornaria 0 e posição > 1}

	{faço p apontar para a cabeça}
	p := cabeca;

	{movo p até o elemento anterior à posição. Como p já
	 está em 1, movo posicao-2 posições}
	FOR i:=1 TO posicao-2 DO
	  p := p^.prox;

	{agora p aponta para o elemento anterior}

	{faço o próximo de q ser o próximo de p}
	q^.prox := p^.prox;

	{faço o próximo de p ser q}
	p^.prox := q
      END
    END
    {ELSE não faz nada!}
  END;
	

Ótimo! Vamos agora excluir um elemento da posição i. Suponha a seguinte lista:

• Primeiro fazemos p apontar para o início da lista:
  
• Em seguida movemos p até o elemento anterior à posição do elemento que queremos excluir (suponha que queremos excluir da 3ª posição):
  
• Marcamos a posição a ser excluída com um ponteiro q:
  
• Fazemos, então, o próximo elemento de p ser o próximo de q:
  
• Eliminamos q:
  

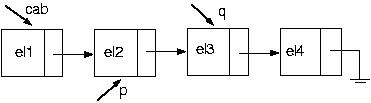
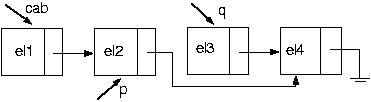
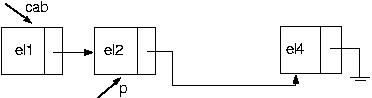
E se a lista estiver vazia? Nesse caso, Nada poderá ser excluído.

E se a posição pedida for 1? Esse, novamente, é um caso um pouco mais complicado, pois não há como parar um elemento antes, o que indica que nosso algoritmo falha. Como fazer, então? Basta seguir o algoritmo dado acima para retirar um elemento do início da lista.

Vamos, então, à função que retira o iº elemento da lista. Essa função retorna o valor que estava nesse elemento:

  FUNCTION TiraDaPos(VAR cabeca:p_no;posicao:integer):tipo;
  VAR p : p_no;    {auxiliar}
      q : p_no;    {auxiliar}
      i : integer; {contador do FOR}
  BEGIN
    {testo se a posição é válida}
    IF (posicao <= NumEl(cabeca)) AND (posicao > 0) THEN
    BEGIN
      {é uma posição válida. Note que se a lista estiver vazia
       nada é feito, pois posicao >=1, o que é > 0}

      {faço p apontar para a cabeça}
      p := cabeca;

      IF posicao=1 THEN {quero na primeira posição}
      BEGIN
	{faço a cabeça ser o segundo elemento}
	cabeca := cabeca^.prox;

	{dou o valor de retorno}
	TiraDaPos := p^.valor;

	{mato o nó}
	Dispose(p)
      END
      ELSE BEGIN {é outra posição}
	{movo p até o elemento anterior à posição. Como p já
	 está em 1, movo posicao-2 posições}
	FOR i:=1 TO posicao-2 DO
	  p := p^.prox;

	{agora p aponta para o elemento anterior}

	{faço o próximo de p ser q}
	q := p^.prox;

	{faço o próximo de p ser o próximo de q}
	p^.prox := q^.prox;

	{retorno o valor de q}
	TiraDaPos := q^.valor;

	{mato o nó apontado por q}
	Dispose(q)
      END
    END
  END;
	

Agora vamos ver como buscar a posição do primeiro elemento que contenha o valor x na nossa lista. Para tal, o procedimento é simples:

• Coloco um ponteiro p na cabeça da lista e crio um contador, inicializando-o com 1.
• Enquanto p não for NIL e não encontrei o valor vou incrementando p e o contador.
• Se encontrei o valor, retorno o valor do contador, senão, retorno 0.

  FUNCTION Pos(cabeca:p_no; elemento:tipo):integer;
  VAR p : p_no;    {auxiliar}
  BEGIN
    {inicializo o contador}
    Pos := 1;

    {aponto p para a cabeça da lista}
    p := cabeça;

    WHILE (p <> NIL) AND (p^.valor <> elemento) DO
    BEGIN
      p := p^.prox;
      Pos := Pos+1
    END;

    IF p = NIL THEN Pos := 0
    {o else é automático, pos terá o valor certo}
  END;
	

E para excluir o primeiro elemento de valor x? Basta

• Buscar a posição do primeiro elemento de valor x
• Excluir o elemento nessa posição

  PROCEDURE ExcluiX(VAR cabeca:p_no; elemento:tipo);
  VAR el : tipo; {o elemento a ser excluído, é auxiliar}
  BEGIN
    el := TiraDaPos(cabeca,Pos(cabeca,elemento))
    {excluí, el jogo fora}
  END;
	

Uma fila é uma lista que tem como característica o fato de que o primeiro elemento a entrar nela é o primeiro a sair. Assim, ela funciona como uma fila comum.

Pense numa fila de banco. Quem será o primeiro a ser atendido? O primeiro que chegou. E onde os que chegam depois devem entrar na fila? No final desta.

Assim é uma fila: se quero retirar um elemento, retiro da frente; se quero incluir, incluo no final da fila.

Note que este foi o modo como implementamos as listas acima, ou seja, quando fazíamos nossa lista, estávamos na verdade construindo uma fila. A única diferença é que em uma fila não posso retirar um elemento do meio da fila, ou lá colocar um, coisa que implementamos acima. Mas, de resto, as funções são as mesmas.

Uma pilha é uma estrutura de dados que, pasmem, funciona como uma pilha!

Pense numa pilha de livros. É assim que ela funciona. Se queremos por mais um livro na pilha, onde colocamos? No topo! E se queremos tirar um livro, de onde tiramos? Do topo.

Então, uma pilha nada mais é do que uma lista ligada que tem como característica o fato de que, se queremos incluir um elemento na lista, temos de incluí-lo no início desta, e se queremos tirar um elemento da lista, tiramos do início desta.

Dessa forma, uma pilha tem as seguintes funções:

• Criação da pilha (como nas listas acima)
• Empilhamento (quando coloco um elemento no topo da pilha, ou seja, no início da lista)
• Desempilhamento (quando tiro um elemento do topo da pilha, ou seja, do início da lista)

É como nossa pilha de livros, para retirar um livro do meio, tenho que desempilhar todos os que estão acima. Da mesma forma, para tirar um dado do meio da pilha, tenho que desempilhar os que estão antes dele. Vejamos, agora, funções para criação, empilhamento e desempilhamento:

  TYPE tipo    = real;
       p_pilha = ^pilha;
       pilha   = RECORD
                   dado : tipo;
		   prox : p_pilha
		 END;

  VAR topo : p_pilha;

  PROCEDURE IniciaPilha(VAR topo : p_pilha);
  BEGIN
    topo := NIL
  END;

  PROCEDURE Empilha(VAR topo : p_pilha; dado : tipo);
  VAR p : p_pilha; {auxiliar}
  BEGIN
    {crio o novo elemento e dou valor a ele}
    new(p);
    p^.valor := dado;

    {faço ele apontar para o topo da pilha}
    p^.prox := topo;

    {faço o topo apontar para ele}
    topo := p
  END;

  FUNCTION Desempilha(VAR topo : p_pilha) : tipo;
  VAR p : p_pilha; {auxiliar}
  BEGIN
    {faço p apontar para o topo}
    p := topo;

    {retorno o valor de p}
    Desempilha := p^.valor;

    {baixo o topo, para o segundo elemento}
    topo := topo^.prox;

    {elimino p}
    Dispose(p)
  END;
       

Acima você encontra ilustrações de como retirar um elemento do início da lista, ou seja, do topo da pilha, e de como incluir um elemento na posição 1 da lista, ou seja, no topo da pilha.

‹— Parte XXV — Página da disciplina — Parte XXVII —›