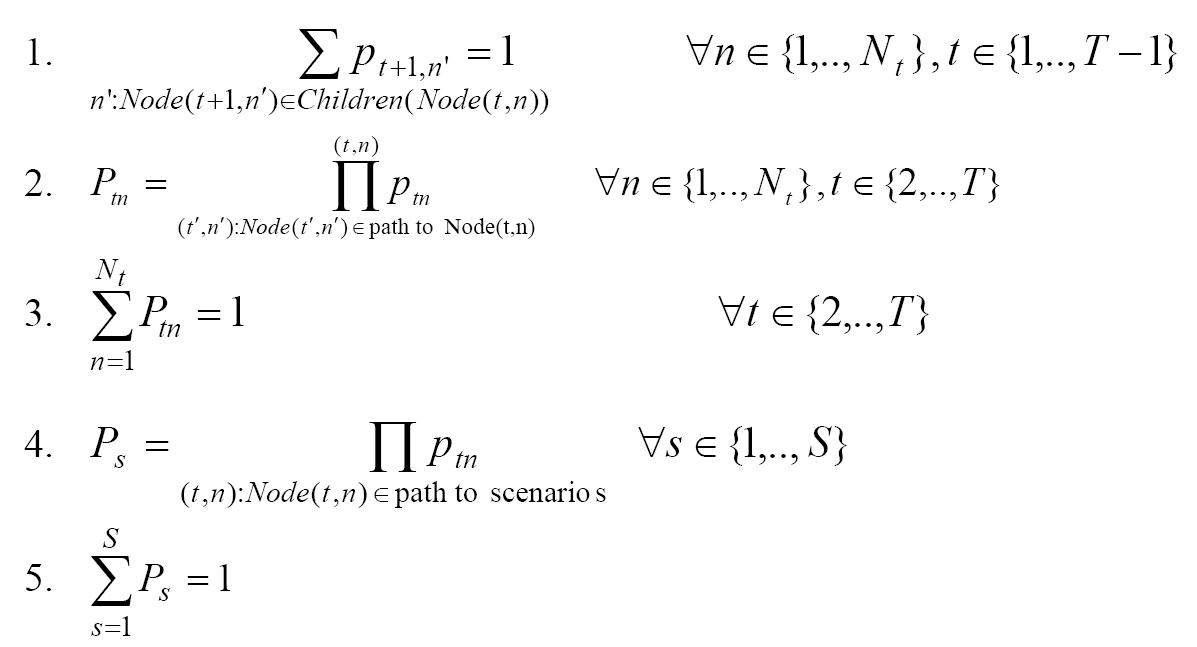Stochastic Programming (SP) basics
Stochastic problems can essentially be divided into 2-stage and multi-stage problems. In a 2-stage problem, the initial decisions are taken first. These are then followed by a random event. Next, the recourse decisions, which are based on this random event, are taken. The multi-stage problem, as the name suggests, consists of multiple stages, with a random event occurring between each stage. In this case, decisions are made at each stage. The following sections give a detailed description of these problems:
2-stage stochastic problems
In a 2-stage problem, first, the initial or the first stage decisions (e.g., system design decisions) are made which are followed by random events such as demand, availability, price, or a combination of these. Then the second stage decisions (e.g. operational decisions) are made. This can be viewed pictorially as follows:

Figure 3.1: 2-stage problem
In the standard form, the 2-stage stochastic program is:
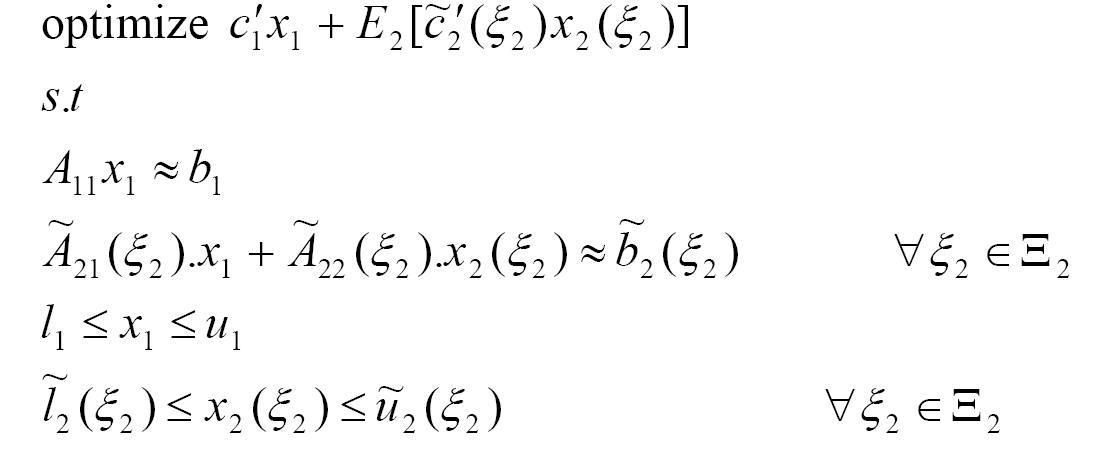
where ![]() indicates
indicates ![]() ,
, ![]() , =
or combination of these. x1 and x2
are the first and the second stage stochastic decision variables
respectively. E2[] is the expectation operator
with respect to the random event
, =
or combination of these. x1 and x2
are the first and the second stage stochastic decision variables
respectively. E2[] is the expectation operator
with respect to the random event ![]() 2.
2.
![]() 2 represents the state space (the set of possible outcomes or
the values that
2 represents the state space (the set of possible outcomes or
the values that ![]() 2
can assume) in the recourse stage. There may be separate values for
the objective coefficients c˜'2(
2
can assume) in the recourse stage. There may be separate values for
the objective coefficients c˜'2(![]() 2),
right hand side b˜2(
2),
right hand side b˜2(![]() 2),
and matrix coefficients Ã21(
2),
and matrix coefficients Ã21(![]() 2)
and Ã22(
2)
and Ã22(![]() 2)
for each outcome
2)
for each outcome ![]() 2
in
2
in ![]() 2,
and the recourse decisions x2(
2,
and the recourse decisions x2(![]() 2)
depend on
2)
depend on ![]() 2,
i.e., there are separate sets of recourse decisions for each outcome
2,
i.e., there are separate sets of recourse decisions for each outcome ![]() 2 in the second stage.
2 in the second stage.
Multi stage stochastic problems
Multi-stage problems can be viewed pictorially as follows:

Figure 3.2: Multi-stage problem
Formally, the multi-stage stochastic program is defined as follows:
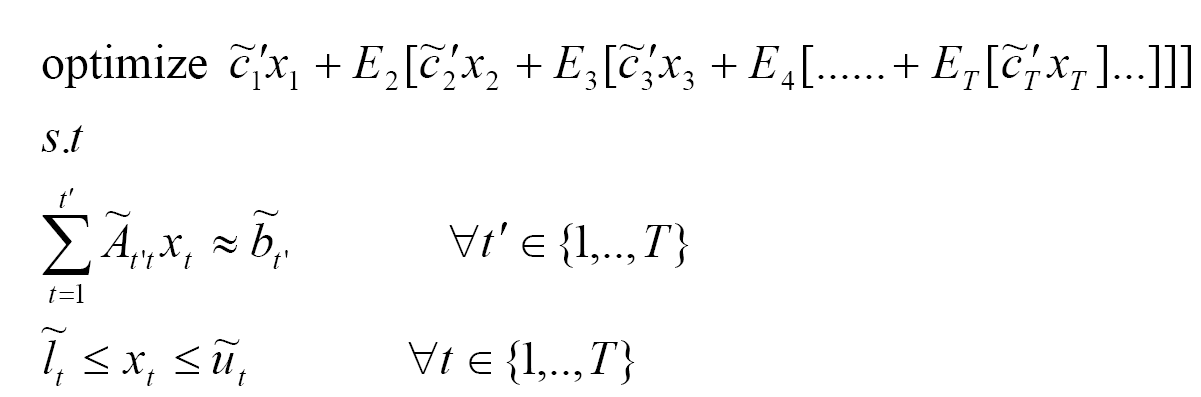
where
`optimize' indicates maximize or minimize
˜ indicates random data variable
![]() indicates
indicates ![]() ,
, ![]() , = or a combination of these
, = or a combination of these
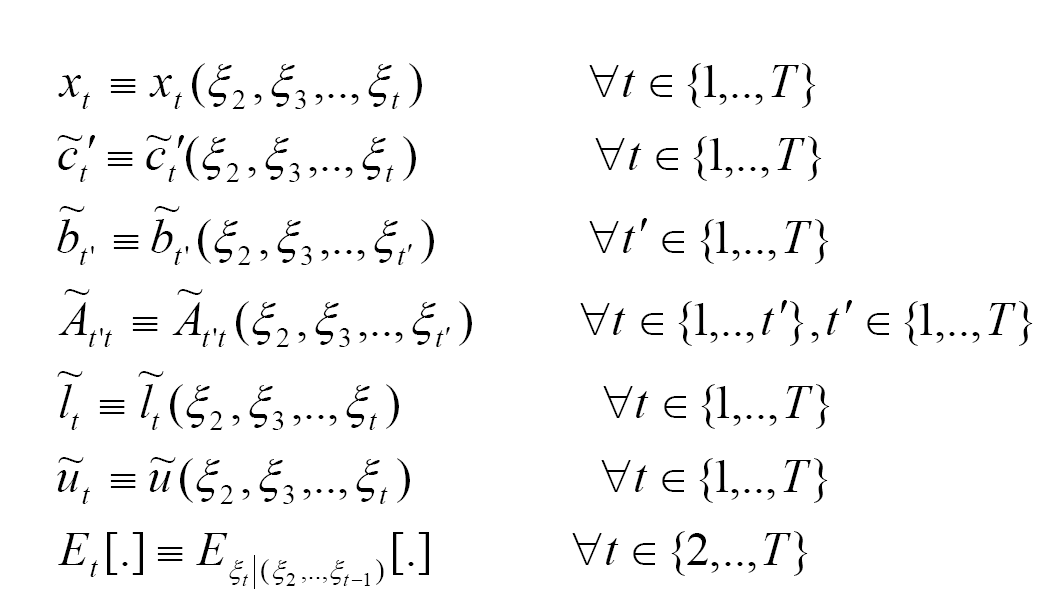
Each of the above entities depends on the sequence of events
(![]() 2,
2,![]() 3,...).—Note that c1, A11, b1, l1,
and u1 are not random.—
3,...).—Note that c1, A11, b1, l1,
and u1 are not random.—
Scenario generation
![]() t
being a random variable, takes different values with different
probabilities. If each of the
t
being a random variable, takes different values with different
probabilities. If each of the ![]() t's can be discretized, the realized values of
t's can be discretized, the realized values of ![]() t give rise to what is called a scenario tree. An
example of a scenario tree with T (number of stages) =3 and S
(number of scenarios) =4 is shown in Figure 3-stage scenario tree.
t give rise to what is called a scenario tree. An
example of a scenario tree with T (number of stages) =3 and S
(number of scenarios) =4 is shown in Figure 3-stage scenario tree.
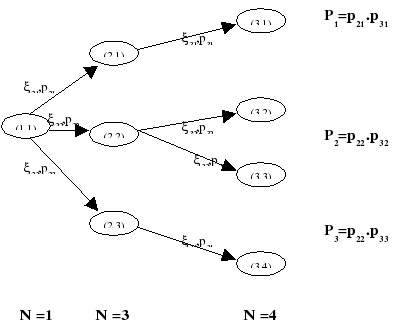
Figure 3.3: 3-stage scenario tree
In the tth stage there are Nt
nodes. For each stage t in 2 to T, each ![]() t
has Nt outcomes (
t
has Nt outcomes (![]() t1 w.p. pt,1,
t1 w.p. pt,1,![]() t2 w.p. pt,2,...
t2 w.p. pt,2,...![]() tNt w.p. pt,Nt),
where ptn is the conditional probability of
visiting the nth node in the tth
stage from its parent node in the t-1th stage. The
realizations of
tNt w.p. pt,Nt),
where ptn is the conditional probability of
visiting the nth node in the tth
stage from its parent node in the t-1th stage. The
realizations of ![]() 2,
2,
![]() 3,...,
3,...,![]() T
correspond to scenarios (paths in the tree). For each stage t
and each node n in that stage, the node has an unconditional
probability Ptn
of being visited, which is equal to the product of conditional
probabilities along the path to that node. Similarly, each scenario
s has a scenario probability Ps that
is equal to the product of conditional probabilities along the path
to that scenario. The following observations can be made about the
scenario tree:
T
correspond to scenarios (paths in the tree). For each stage t
and each node n in that stage, the node has an unconditional
probability Ptn
of being visited, which is equal to the product of conditional
probabilities along the path to that node. Similarly, each scenario
s has a scenario probability Ps that
is equal to the product of conditional probabilities along the path
to that scenario. The following observations can be made about the
scenario tree:
Underlying deterministic model
If we ignored the randomness of the data momentarily, then an underlying deterministic model can be written as follows:

Expanding the underlying deterministic model
Given the dependency of the coefficients (c˜t,Ãtt',b˜t,l˜t,u˜t)
of a stochastic program on the random events (![]() t),
it can automatically be expanded into an extensive form
(deterministic equivalent problem) by introducing new variables and
constraints. There are basically two ways of creating new variables
and constraints: node based and scenario based.
t),
it can automatically be expanded into an extensive form
(deterministic equivalent problem) by introducing new variables and
constraints. There are basically two ways of creating new variables
and constraints: node based and scenario based.
Node based
Given a scenario tree, the underlying deterministic model can be expanded into an extensive mathematical program based on the nodes. The basic idea is to add a subscript of a node number to each of the stochastic decision variables (xt becomes xt,n for n=1,...,Nt). Then the resulting extensive deterministic model would be:

In this model ctn,Att'n,btn,ltn,utn are the resolved values of c˜t,Ãtt',b˜t,l˜t,u˜t at the node(t,n). Based on above formulation, the matrix structure of the problem shown in Figure 3-stage scenario tree would look as follows:

Figure 3.4: Node based matrix
Scenario based
A stochastic model can also be expanded based on the scenarios. Here
each variable is also subscripted by scenarios (xt ![]() xt,s
for s=1,...,S). The expanded mathematical program would
look as follows:
xt,s
for s=1,...,S). The expanded mathematical program would
look as follows:

Here cts,Att's,bts,lts,uts are realizations of c˜t,Ãtt',b˜t,l˜t,u˜t respectively in scenario s.
Non-anticipative constraints (NAC)
Consider
the node(2,2) in Figure 3-stage scenario tree. When the model is parsed according to
scenarios, although we have two separate variables x22
and x23 corresponding to scenarios 2 and 3 at this
node, both of them should assume same value since they cannot depend
on the future events (xt ![]() xt(
xt(![]() s,...,
s,...,![]() t)).
Therefore, the following set of non-anticipative constraints also
needs to be included in the above formulation:
t)).
Therefore, the following set of non-anticipative constraints also
needs to be included in the above formulation:
xts = xts' ![]() n
n ![]() {1,...,Nt}, t
{1,...,Nt}, t ![]() {1,...,T-1}, s
{1,...,T-1}, s ![]() s'
s' ![]()
![]() tn,
where
tn,
where ![]() tn
is the set of scenarios passing through the node(t,n). Hence,
the matrix structure for the problem shown in Figure 3-stage scenario tree would look as follows.
tn
is the set of scenarios passing through the node(t,n). Hence,
the matrix structure for the problem shown in Figure 3-stage scenario tree would look as follows.

Figure 3.5: Scenario based matrix
Solution measures
Recourse problem (R.)
The standard stochastic problem discussed in Section Multi stage stochastic problems is also referred to as the recourse problem.

Expected Value problem
If the ![]() t's
are replaced by their expected values in the recourse problem, then
such a problem is called an expected value (EV) problem.
t's
are replaced by their expected values in the recourse problem, then
such a problem is called an expected value (EV) problem.

where,

Expected Value problem with recourse
Let x- = (x-1,x-2,...x-T) be the optimal solution to the above problem, then for each stage an expected recourse problem can be defined as follows.

Here, the first t stage variables are fixed at their optimal values obtained in the EV problem. The following observations can be made:
- zEV is not worse than zR
(i.e., if maximizing, zEV
 zR).
zR).
- If
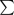
Ãt't''x-t't t''=1  b˜t', l˜t'
b˜t', l˜t'  x-t'
x-t'  u˜t'
u˜t' 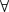 t'
t' {1,...,t}
and EVrt is feasible then, zR is
not worse than zEVr(t).
{1,...,t}
and EVrt is feasible then, zR is
not worse than zEVr(t).
- If 2. is true then the value of stochastic solution:
VSS(t) is the absolute value of the difference between
zR and zEVr(t),
else it is +
 .
.
Perfect Information problem
Here, the problem for each scenario is solved independently.

Let x*s = (x*1s,x*2s,...,x*Ts) be the optimal solution to the above problem,
x* = ![]()
Psx*s = (x*1,x*2,...,x*T)
be the aggregated solution, and zPI =
S
s=1
![]()
PszPI(s)
be the aggregated objective value.
S
s=1
Perfect information problem with recourse

The following observations can be made:
- ZPI is not worse than ZRP.
-
If
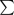
Ãt't''x*t't t''=1  b˜t', l˜t'
b˜t', l˜t'  x*t'
x*t'  u˜t'
u˜t'  t'
t' {1,...,t}
and PIrt is feasible then,
ZPI is not worse than ZPIr(t).
{1,...,t}
and PIrt is feasible then,
ZPI is not worse than ZPIr(t).
- If 2. is true
then the expected value of perfect information: EVPI
is the absolute value of the difference between ZR and
ZPI, else it is
+
 .
.
Focus on an instance of the problem
Instead of looking at the fully expanded problem at once, one could also look at the instance of the underlying problem in a particular scenario or at a node in a scenario tree. The corresponding
model in a scenario s
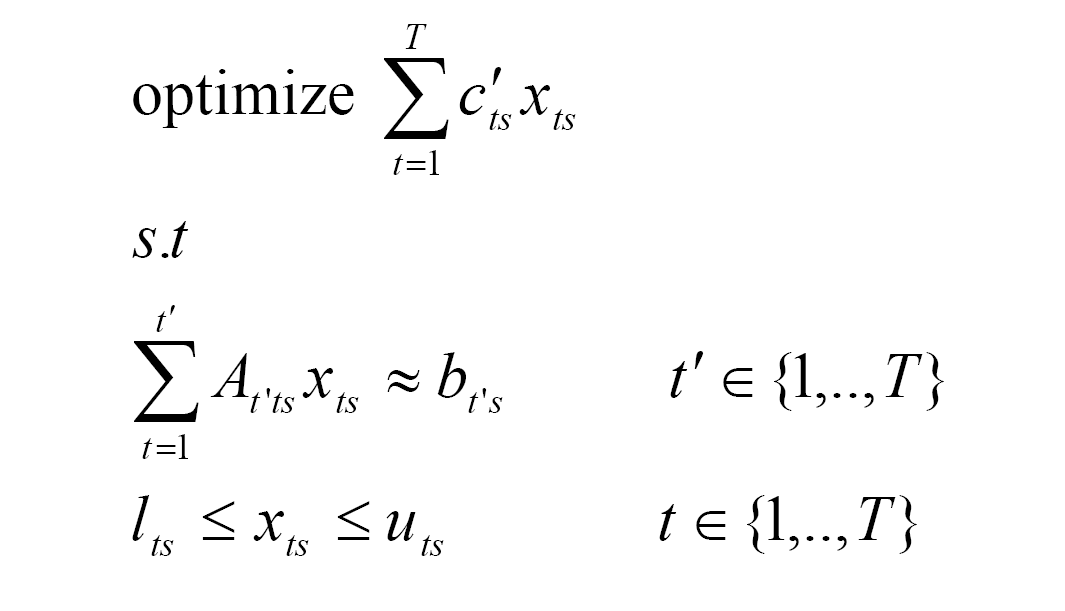
model at a node(t,n) in the scenario tree

e.g. in Figure 3-stage scenario tree the model focused at node(3,4) will be:
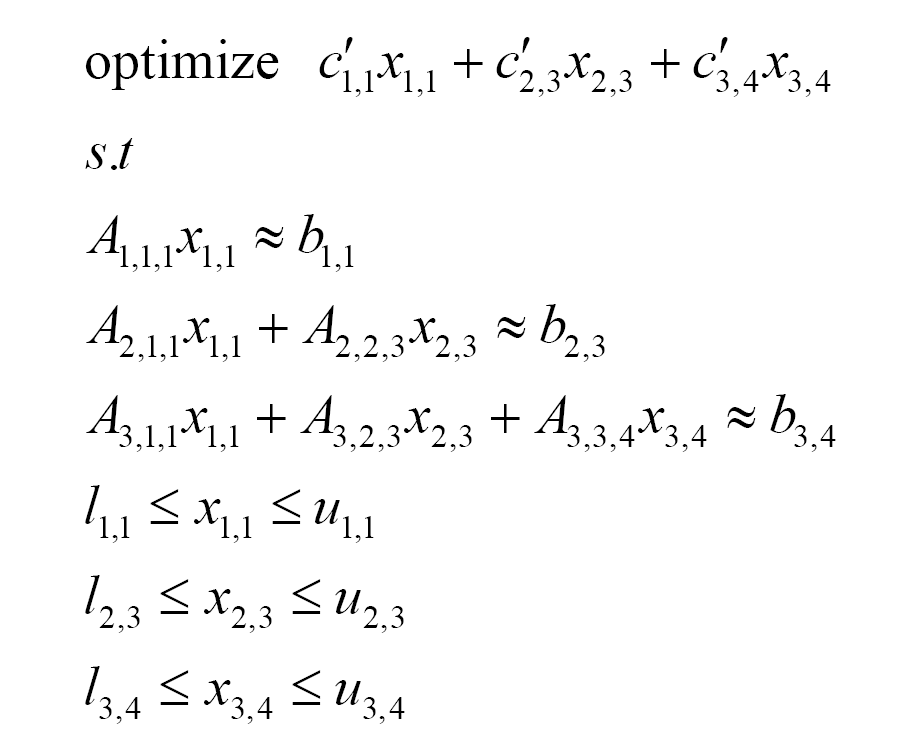
If you have any comments or suggestions about these pages, please send mail to docs@dashoptimization.com.